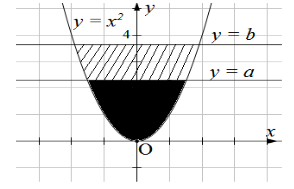
Trong hệ trục tọa độ \(Oxy\), cho parabol \(\left( P \right):y = {x^2}\) và hai đường thẳng \(y = a\), \(y = b\) \(\left( {0 < a < b} \right)\) (hình vẽ). Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi parabol \(\left( P \right)\) và đường thẳng \(y = a\) (phần tô đen); \(\left( {{S_2}} \right)\) là diện tích hình phẳng giới hạn bởi parabol \(\left( P \right),\) đường thẳng $y=a$ và đường thẳng \(y = b\) (phần gạch chéo). Với điều kiện nào sau đây của \(a\) và \(b\) thì \({S_1} = {S_2}\)?

Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t) = \dfrac{1}{{150}}{t^2} + \dfrac{{59}}{{75}}t(\;m/s)\), trong đó \(t\) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn 3 giây so với \(A\) và có gia tốc bằng \(a\left( {\;m/{s^2}} \right)\) ( \(a\) là hằng số). Sau khi \(B\) xuất phát được 12 giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng

Dòng điện xoay chiều hình sin chạy qua mạch dao động LC lí tưởng có phương trình \(i = {I_0}\sin \left( {wt + \dfrac{\pi }{2}} \right)\). Ngoài ra \(i = {q^\prime }(t)\) với \(q\) là điện tích tức thời trong tụ. Tính từ lúc \(t = 0\), điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian \(\dfrac{\pi }{{2w}}\) là

Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right) = 3\) và \(f\left( x \right) + f\left( {2 - x} \right) = {x^2} - 2x + 2\,\,\forall x \in \mathbb{R}\). Tích phân \(\int\limits_0^2 {xf'\left( x \right)dx} \) bằng:

Cho \(f\left( x \right)\) là hàm liên tục trên đoạn \(\left[ {0;a} \right]\) thỏa mãn \(\left\{ {\begin{array}{*{20}{c}}{f\left( x \right).f\left( {a - x} \right) = 1}\\{f\left( x \right) > 0,\forall x \in \left[ {0;a} \right]}\end{array}} \right.\) và \(\int\limits_0^a {\dfrac{{{\rm{d}}x}}{{1 + f\left( x \right)}}}  = \dfrac{{ba}}{c},\) trong đó \(b\), \(c\) là hai số nguyên dương và \(\dfrac{b}{c}\) là phân số tối giản. Khi đó \(b + c\) có giá trị thuộc khoảng nào dưới đây?

Một chất điểm đang chuyển động với vận tốc \({v_0} = 15\;{\rm{m/s}}\) thì tăng tốc với gia tốc \(a\left( t \right) = {t^2} + 4t\;\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường chất điểm đó đi được trong khoảng thời gian \(3\) giây kể từ lúc bắt đầu tăng vận tốc.

Bác Năm làm một cái cửa nhà hình parabol bằng gỗ có chiều cao từ mặt đất đến đỉnh là \(2,25\) mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá tiền mỗi mét vuông gỗ là \(1500000\) đồng. Vậy số tiền bác Năm phải trả là:

Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = {{\rm{e}}^{x - 1}}\), các trục tọa độ và phần đường thẳng \(y = 2 - x\) với \(x \ge 1\). Tính thể tích khối tròn xoay tạo thành khi quay  quanh trục hoành.