Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định với mọi \(x \in \mathbb{R}\)
Hàm số nào dưới đây có tập xác định \(\mathbb{R}\)?
Đáp án A: Hàm số xác định khi \(x \ne 0\) nên TXĐ \(D = \mathbb{R}\backslash \left\{ 0 \right\}\) loại.
Đáp án B: Hàm số đa thức bậc ba xác định trên \(\mathbb{R}\) thỏa mãn.
Đáp án C: Hàm số xác định khi \(x - 1 \ge 0 \Leftrightarrow x \ge 1\) suy ra TXĐ \(D = \left[ {1; + \infty } \right)\) loại.
Đáp án D: Hàm số xác định nếu \(x \ne 0\) nên TXĐ \(D = \mathbb{R}\backslash \left\{ 0 \right\}\) loại.
Số điểm cực trị của hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) có thể có nhiều nhất mấy điểm cực trị?
Hàm đa thức bậc ba chỉ có thể có 2 cực trị hoặc không có cực trị nào nên số điểm cực trị nhiều nhất có thể có là \(2\)
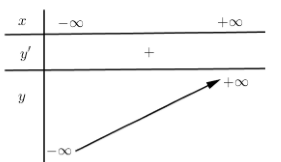
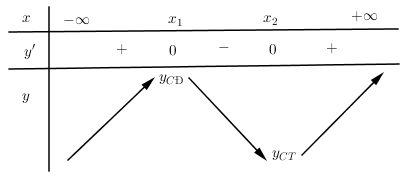
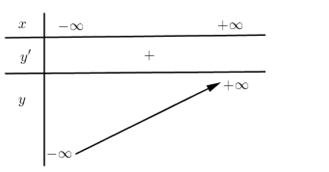
Hàm đa thức bậc ba đồng biến trên \(\mathbb{R}\) có thể có bảng biến thiên dạng nào dưới đây?
Hàm đa thức bậc ba đồng biến trên \(\mathbb{R}\) thì \(y' \ge 0,\forall x \in \mathbb{R}\)
Quan sát các bbt ta thấy đáp án D thỏa mãn.
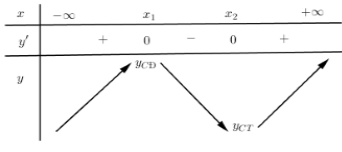
Cho bảng biến thiên hình bên, hàm số đồng biến trên:
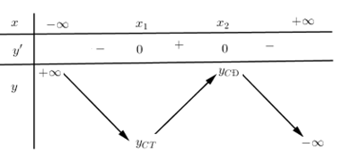
Quan sát bảng biến thiên ta thấy \(y' > 0,\forall x \in \left( {{x_1};{x_2}} \right)\) nên hàm số nghịch biến trên khoảng \(\left( {{x_1};{x_2}} \right)\)
Tâm đối xứng của đồ thị hàm số bậc ba có hoành độ là nghiệm của phương trình
Tâm đối xứng của đồ thị hàm số bậc ba có hoành độ là nghiệm của phương trình \(y'' = 0\)
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
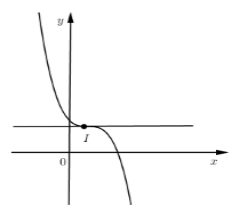
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \) nên \(a < 0\).
Đồ thị hàm số bậc ba luôn
- Đồ thị hàm số bậc ba có thể cắt trục hoành tại \(1,2\) hoặc \(3\) điểm nên A đúng.
Ngoài ra các đáp án còn lại đều không đúng.
Chọn kết luận đúng:
- Hàm số bậc ba có 2 điểm cực trị thì đồ thị có thể cắt trục hoành tại \(1,2\) hoặc 3 điểm nên C, D sai.
- Đồ thị hàm số bậc ba cắt trục hoành tại \(1\) điểm duy nhất thì nó có thể có \(2\) điểm cực trị hoặc không có điểm cực trị nào.
Nếu điểm cực tiểu của đồ thị hàm số bậc ba nằm ở trục hoành thì:
Hàm số bậc ba luôn có \({y_{CD}} > {y_{CT}}\) nên nếu \({y_{CT}} = 0\) thì \({y_{CD}} > 0\).
Do đó điểm cực đại nằm phía trên trục hoành..
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\). Biết \(\left( C \right)\) chỉ có \(2\) điểm chung với trục hoành. Chọn kết luận đúng:
Quan sát các dáng đồ thị của hàm số bậc ba:
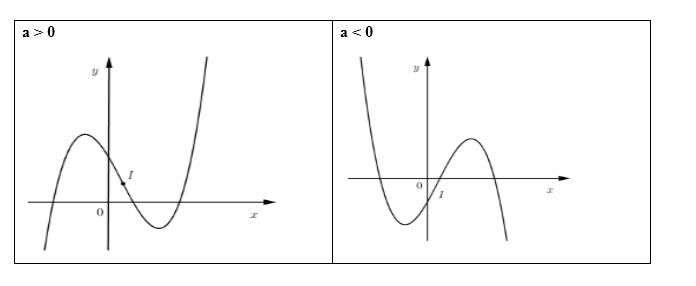
Ta thấy đồ thị hàm số bậc ba chỉ có \(2\) điểm chung với trục hoành nếu một trong hai điểm cực trị của đồ thị hàm số nằm trên trục hoành hay một trong hai điểm cực trị của hàm số là nghiệm của phương trình \(f\left( x \right) = 0\)
Cho hàm số \(y = f\left( x \right)\) có hai giá trị cực đại, cực tiểu thỏa mãn \({y_{CD}}.{y_{CT}} = 0\). Khi đó:
Vì \({y_{CD}}.{y_{CT}} = 0 \Leftrightarrow \left[ \begin{array}{l}{y_{CD}} = 0\\{y_{CT}} = 0\end{array} \right.\) hay một trong hai điểm cực trị của đồ thị hàm số nằm trên trục hoành.
Khi đó đồ thị hàm số chỉ có \(2\) giao điểm chung với \(Ox\)
Cho đồ thị hàm số bậc ba \(y = f\left( x \right)\) có hai điểm cực trị thỏa mãn \({y_{CT}} > 0\). Khi đó, đồ thị hàm số có mấy điểm chung với trục \(Ox\)?
Hai đạng đồ thị hàm số bậc ba mà có hai cực trị là:
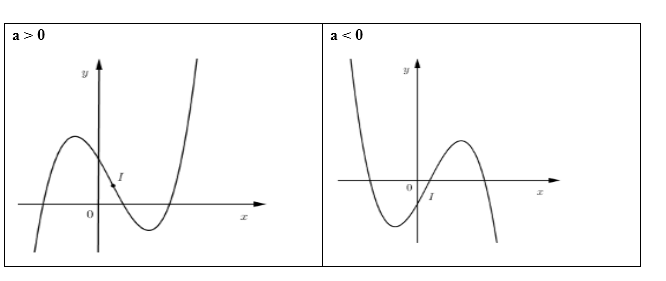
Do \({y_{CT}} > 0\) nên \({y_{CD}} > {y_{CT}} > 0\) hay hai điểm cực trị của đồ thị hàm số đều nằm phía trên trục hoành.
Từ đó đồ thị hàm số chỉ có \(1\) điểm chung duy nhất với \(Ox\).
Chọn kết luận đúng:
Đáp án A: Đồ thị hàm số bậc ba luôn có điểm uốn nhưng chưa chắc thuộc trục tung nên A sai.
Đáp án B: Đồ thị hàm số bậc ba không có trục đối xứng nên B sai.
Đáp án C: Điểm uốn chính là tâm đối xứng của đồ thị hàm số bậc ba nên với mỗi điểm thuộc đồ thị, lấy đối xứng qua điểm đó ta cũng được một điểm thuộc đồ thị nên C đúng.
Đáp án D: Đồ thị hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) luôn chỉ có một điểm chung duy nhất với \(Oy\) nên D sai.
Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:
Hàm đa thức bậc ba xác định trên $R$.
Hàm đa thức bậc ba có thể có mấy cực trị?
$y' = 0$ có hai nghiệm phân biệt ${x_1},{x_2} \Rightarrow $ có $2$ cực trị.
$y' = 0$ vô nghiệm hoặc có nghiệm kép $ \Rightarrow $ không có cực trị.
Do đó hàm đa thức bậc ba chỉ có thể có $2$ cực trị hoặc không có cực trị nào.
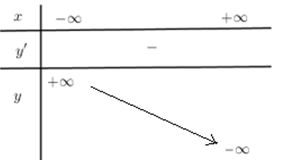
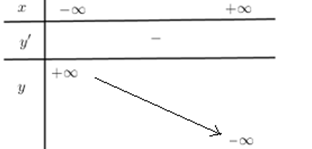
Hàm đa thức bậc ba không có cực trị và nghịch biến có bảng biến thiên dạng nào dưới đây?
Hàm đa thức bậc ba không có cực trị và nghịch biến thì đạo hàm $y'$ mang dấu âm với mọi $x \in \left( { - \infty ; + \infty } \right)$.
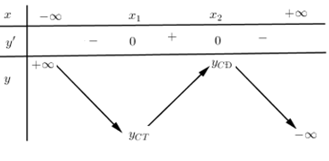
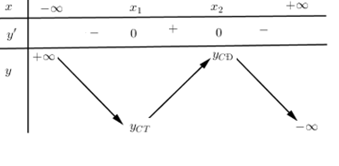
Cho bảng biến thiên hình bên, hàm số nghịch biến trên:
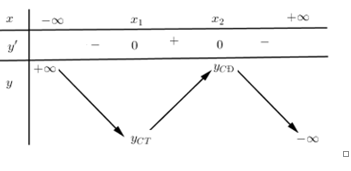
Quan sát bảng biến thiên ta thấy $y' < 0,\forall x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ;{x_1}} \right)$ và $\left( {{x_2}; + \infty } \right)$.
Đồ thị hàm số bậc ba có mấy tâm đối xứng?
Phương trình $y'' = 0$ luôn có nghiệm duy nhất nên đồ thị hàm số bậc ba luôn có 1 điểm uốn hay 1 tâm đối xứng duy nhất.
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
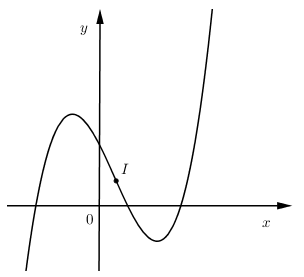
Quan sát đồ thị ta thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ nên $a > 0$.