Bài tập ôn tập chương 2

Gọi khối lượng công việc công ty xây dựng đã làm được trong tháng thứ nhất là \(x(x > 0)\).

Nếu theo đúng tiến độ như tháng thứ nhất thì công trình hoàn thành sau đúng 23 tháng nữa nên tổng khối lượng công việc phải hoàn thành là 24x.

Để sớm hoàn thành công việc thì khối lượng công việc mỗi tháng công ty xây dựng phải làm lập thành cấp số nhân có số hạng đầu \({u_1} = x\), công bội \(q = 1,04\).

Giả sử công trình được hoàn thành ở tháng thứ \(n\) sau khi khởi công.

Ta có phương trình: \(x \cdot \dfrac{{1,{{04}^n} - 1}}{{0,04}} = 24x\)\( \Leftrightarrow 1,{04^n} = 1 + 24.0,04\)\( \Leftrightarrow n \simeq 17,158\).

Vậy công trình được hoàn thành ở tháng thứ 18 sau khi khởi công.

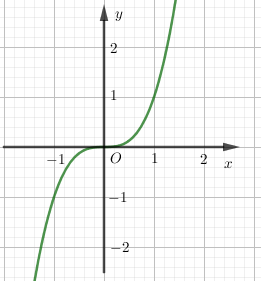
Đồ thị của hình vẽ là đồ thị hàm bậc ba \(y = {x^3}\)

Ta có: ${\log _2}2016 = {\log _2}\left( {{2^5}{3^2}7} \right)$$ = {\log _2}{2^5} + {\log _2}{3^2} + {\log _2}7$$ = 5 + 2a + b$.

$\begin{array}{l}P = \ln \left( {\tan 1{\rm{^\circ }}} \right) + \ln \left( {\tan 2^\circ } \right) + \ln \left( {\tan 3^\circ } \right) + ... + \ln \left( {\tan 89^\circ } \right)\\ = \ln \left( {\tan 1^\circ .\tan 2^\circ .\tan 3^\circ ...\tan 89^\circ } \right)\\= \ln \left( {\tan 1^\circ .\tan 2^\circ .\tan 3^\circ ...\tan 45^\circ .\cot 44^\circ .\cot 43^\circ ...\cot 1^\circ } \right)\end{array}$

$= \ln \left( {\tan 45^\circ } \right) = \ln 1 = 0.$ (vì \(\tan \alpha .\cot \alpha  = 1\))

Ta có $\ln a.\ln b = \ln b.\ln a \Leftrightarrow \ln \left( {{b^{\ln a}}} \right) = \ln \left( {{a^{\ln b}}} \right) \Leftrightarrow {b^{\ln a}} = {a^{\ln b}}$

Cơ số \(\dfrac{{e + 1}}{\pi } > 1\) nên hàm số mũ \(y = {\left( {\dfrac{{e + 1}}{\pi }} \right)^x}\) đồng biến trên \(\mathbb{R}\).

Ta có: $y' = {e^x} - {e^{ - x}} \Rightarrow y'' = {e^x} + {e^{ - x}} \Rightarrow y''\left( 1 \right) = e + \dfrac{1}{e}$.

Điều kiện xác định của hàm số \(y = {({x^2} - 16)^{ - 5}} - \ln (24 - 5x - {x^2})\) là :

\(\left\{ \begin{array}{l}{x^2} - 16 \ne 0\\24 - 5x - {x^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm 4\\ - 8 < x < 3\end{array} \right.\)

Vậy tập xác định là : \(D = ( - 8;3)\backslash \left\{ { - 4} \right\}\).

Hàm số có tập xác định $D = \mathbb{R}$ khi ${4^x} - {2^x} + m > 0,\left( 1 \right)$, $\forall x \in R$

Đặt $t = {2^x}$, $t > 0$

Khi đó $\left( 1 \right)$ trở thành ${t^2} - t + m > 0$$ \Leftrightarrow m >  - {t^2} + t$, $\forall t \in \left( {0; + \infty } \right)$

Đặt $f\left( t \right) =  - {t^2} + t$

ycbt  xảy ra khi $m > \mathop {Max}\limits_{\left( {0; + \infty } \right)} f\left( t \right) = \dfrac{1}{4}$.

Với $x >  - \dfrac{1}{4}$.

Áp dụng công thức ${\left( {{{\log }_a}u} \right)^\prime } = \dfrac{{u'}}{{u\ln a}}$ ta có $y' = \dfrac{4}{{\left( {4x + 1} \right)\ln 3}}.$

Điều kiện $\left\{ \begin{array}{l}x > 0\\{\log _2}x > 0\\{\log _8}x > 0\end{array} \right. \Leftrightarrow x > 1$

Đặt \(t = {\log _2}x,\left( {t > 0} \right)\)

Tacó: \({\log _2}\left( {{{\log }_8}x} \right) = {\log _8}\left( {{{\log }_2}x} \right) \Rightarrow {\log _2}\left( {\dfrac{1}{3}t} \right) = \dfrac{1}{3}{\log _2}\left( t \right)\)\( \Rightarrow \dfrac{1}{3}t = {t^{\dfrac{1}{3}}}\)\( \Rightarrow \left[ \begin{array}{l}{t^2} = 27\\t = 0,\left( {loai} \right)\end{array} \right.\)\( \Rightarrow P = 27\).\(\)

Ta có: \({\log _9}6 = \dfrac{{{{\log }_2}6}}{{{{\log }_2}9}} = \dfrac{{{{\log }_2}6}}{{2{{\log }_2}3}} = \dfrac{{{{\log }_2}6}}{{2\left( {{{\log }_2}6 - {{\log }_2}2} \right)}} = \dfrac{m}{{2\left( {m - 1} \right)}}\).

Ta có: \({\log _2}x + {\log _2}y = {\log _2}\left( {xy} \right)\) nên D sai, các đáp án còn lại đều đúng theo công thức logarit.

Đặt $t = {2^x},\left( {t > 0} \right)$.

Phương trình đã cho trở thành ${t^2} - 6t + 8 = 0$$ \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = 4\end{array} \right.$

Với $t = 2 \Rightarrow {2^x} = 2 \Leftrightarrow x = 1$.

Với $t = 2 \Rightarrow {2^x} = 4 \Leftrightarrow x = 2$.

Vậy phương trình có hai nghiệm $x_1 = 1$ và $x_2 = 2.$

\({\log _{\sqrt[4]{2}}}{\left( {{x^2} - 2} \right)^2} = 8\)\(\left( 1 \right)\)

\( \Rightarrow \) ĐK: \({x^2} - 2 \ne 0 \Leftrightarrow x \ne  \pm \sqrt 2 \)

\(\left( 1 \right) \Rightarrow {\left( {{x^2} - 2} \right)^2} = {\left( {\sqrt[4]{2}} \right)^8}\)

\( \Leftrightarrow {\left( {{x^2} - 2} \right)^2} = 4=2^2\)

\(\Leftrightarrow \left[ \begin{array}{l}{x^2-2} = 2\\{x^2}-2 = -2\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}{x^2} = 4\\{x^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 2 \\ x = 2\\x = 0.\end{array} \right.\)

${\left( {\sqrt 5  - 2} \right)^{\dfrac{{2x}}{{x - 1}}}} \le {\left( {\sqrt 5  + 2} \right)^x}$$ \Leftrightarrow {\left( {\sqrt 5  + 2} \right)^{\dfrac{{ - 2x}}{{x - 1}}}} \le {\left( {\sqrt 5  + 2} \right)^x}$$ \Leftrightarrow  - \dfrac{{2x}}{{x - 1}} \le x$

$ \Leftrightarrow \dfrac{{2x}}{{x - 1}} + x \ge 0$$ \Leftrightarrow \dfrac{{{x^2} + x}}{{x - 1}} \ge 0 \Leftrightarrow  - 1 \le x \le 0 \vee x > 1$ .

Hàm số \(y = {7^x}\) đồng biến trên \(R\). 

Hàm số \(y = 10 - 3x\) nghịch biến trên \(R\).

Phương trình \({7^x} = 10 - 3{x}\) có nghiệm duy nhất \(x = 1\) nên:

+ Nếu $x\ge 1$ thì $7^x\ge 7 \ge 10-3x$ hay bất phương trình luôn đúng với $x \ge 1$.

+ Nếu $x< 1$ thì $7^x< 7 < 10-3x$ hay bất phương trình không thỏa với $x < 1$

Vậy bất phương trình đã cho có nghiệm $[1;+\infty )$

Ta có: \(x + 2 > 0 \Leftrightarrow x >  - 2\).

Vậy TXĐ của hàm số là: \(D = ( - 2; + \infty )\)

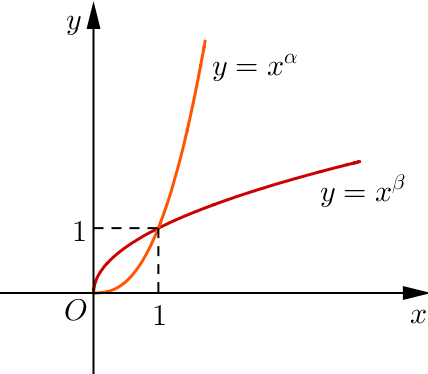
Với \({x_0} > 1\) ta có:

\(x_0^\alpha  > 1 \Rightarrow \alpha  > 0;x_0^\beta  > 1 \Rightarrow \beta  > 0\).

\(x_0^\alpha  > x_0^\beta  \Rightarrow \alpha  > \beta \)

Mặt khác, dựa vào hình dáng đồ thị ta suy ra \(\alpha  > 1\) và \(\beta  < 1\)

Từ đó suy ra A là phương án đúng.

\({\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1 \) \(\Leftrightarrow 0 < {\log _{\frac{1}{2}}}x < 3 \) \(\Leftrightarrow 1 > x > {\left( {\dfrac{1}{2}} \right)^3}\) \( \Leftrightarrow \dfrac{1}{8} < x < 1\)