Một người gửi tiết kiệm với lãi suất \(6,5\% \) năm và lãi hàng năm được nhập vào vốn. Hỏi khoảng bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
Gọi là $x$ số tiền gửi ban đầu.
Giả sử sau $n$ năm số tiền vốn và lãi là $2x$.
Ta có $2x \approx x.{\left( {1,065} \right)^n} \Leftrightarrow {\left( {1,065} \right)^n} \approx 2 \Leftrightarrow n \approx {\log _{1,065}}2 \Leftrightarrow n \approx 11.$
Với giá trị nào của $x$ để hàm số $y = {2^{2{{\log }_3}x - \log _3^2x}}$ đạt giá trị lớn nhất?
Tập xác định của hàm số \(y = {2^{2{{\log }_3}x - \log _3^2x}}\) là \(D = \left( {0; + \infty } \right)\).
Ta có:
\(y' = {\left( {{2^{2{{\log }_3}x - \log _3^2x}}} \right)^\prime } = \left( {\dfrac{2}{{x\ln 3}} - \dfrac{{2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2 = \left( {\dfrac{{2 - 2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2\)
\(y' = 0 \Leftrightarrow \left( {\dfrac{{2 - 2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2 = 0 \) \(\Leftrightarrow {\log _3}x = 1 \Leftrightarrow x = 3\)
Bảng biến thiên:
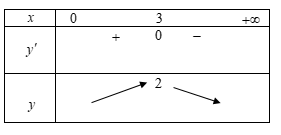
Dựa và bảng biến thiên ta có hàm số \(y = {2^{2{{\log }_3}x - \log _3^2x}}\) đạt giá trị lớn nhất bằng \(2\) tại \(x = 3\)
Có bao nhiêu giá trị thực của tham số \(m\) để phương trình \(m{.3^{{x^2} - 3x + 2}} + {3^{4 - {x^2}}} = {3^{6 - 3x}} + m\) có đúng \(3\) nghiệm thực phân biệt.
Đặt $\left\{ \begin{array}{l}{3^{{x^2} - 3x + 2}} = u\\{3^{4 - {x^2}}} = v\end{array} \right. \Rightarrow u.v = {3^{6 - 3x}}$.
Khi đó phương trình trở thành:
$\begin{array}{l}mu + v = uv + m \Leftrightarrow m\left( {u - 1} \right) - v\left( {u - 1} \right) = 0 \\\Leftrightarrow \left( {u - 1} \right)\left( {m - v} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}u = 1\\v = m\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}{3^{^{{x^2} - 3x + 2}}} = 1\\{3^{4 - {x^2}}} = m\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}{x^2} - 3x + 2 = 0\\4 - {x^2} = {\log _3}m\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\\{x^2} = 4 - {\log _3}m\,\,(*)\end{array} \right.\end{array}$
Để phương trình có ba nghiệm thì ${x^2} = 4 - {\log _3}m$ có một nghiệm duy nhất khác $1;2$ hoặc có hai nghiệm phân biệt, trong đó có một nghiệm bằng 1 hoặc 2, nghiệm còn lại khác 1 và 2.
TH1: (*) có nghiệm duy nhất $x=0$.
Tức $4 - {\log _3}m = 0 \Leftrightarrow m = 81$.
TH2: (*) có một nghiệm x=1 thì
\({1^2} = 4 - {\log _3}m\)\( \Leftrightarrow {\log _3}m = 3 \Leftrightarrow m = 27\)
Khi đó pt (*) là \({x^2} = 1 \Leftrightarrow x = \pm 1\) thỏa mãn yêu cầu.
TH3: (*) có nghiệm x=2. Khi đó \({2^2} = 4 - {\log _3}m\)\( \Leftrightarrow {\log _3}m = 0 \Leftrightarrow m = 1\)
Khi đó pt (*) là \({x^2} = 4 \Leftrightarrow x = \pm 2\) thỏa mãn yêu cầu.
Vậy \(m \in \left\{ {81;27;1} \right\}\)
Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt: \({\log _3}(1 - {x^2}) + {\log _{\frac{1}{3}}}(x + m - 4) = 0\).
\({\log _3}(1 - {x^2}) + {\log _{\frac{1}{3}}}(x + m - 4) = 0 \Leftrightarrow \left\{ \begin{array}{l}1 - {x^2} > 0\\{\log _3}(1 - {x^2}) = {\log _3}(x + m - 4)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \left( { - 1;1} \right)\\1 - {x^2} = x + m - 4\end{array} \right.\)
Yêu cầu bài toán\( \Leftrightarrow f\left( x \right) = {x^2} + x + m - 5 = 0\) có 2 nghiệm phân biệt \( \in \left( { - 1;1} \right)\)
Cách 1: Dùng định lí về dấu tam thức bậc hai.
Để thỏa yêu cầu bài toán ta phải có phương trình \(f\left( x \right) = 0\) có hai nghiệm thỏa: \( - 1 < {x_1} < {x_2} < 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}a.f\left( { - 1} \right) > 0\\a.f\left( 1 \right) > 0\\\Delta > 0\\ - 1 < \dfrac{S}{2} < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 5 > 0\\m - 3 > 0\\21 - 4m > 0\end{array} \right. \) \(\Leftrightarrow 5 < m < \dfrac{{21}}{4}\)
Hỏi phương trình \({3.2^x} + {4.3^x} + {5.4^x} = {6.5^x}\) có tất cả bao nhiêu nghiệm thực?
\(pt \Leftrightarrow 3.{\left( {\dfrac{2}{5}} \right)^x} + 4.{\left( {\dfrac{3}{5}} \right)^x} + 5.{\left( {\dfrac{4}{5}} \right)^x} - 6 = 0\)
Xét hàm số \(f\left( x \right) = 3.{\left( {\dfrac{2}{5}} \right)^x} + 4.{\left( {\dfrac{3}{5}} \right)^x} + 5.{\left( {\dfrac{4}{5}} \right)^x} - 6\) liên tục trên \(\mathbb{R}\).
Ta có: \(f'\left( x \right) = 3 \cdot {\left( {\dfrac{2}{5}} \right)^x} \cdot \ln \dfrac{2}{5} + 4 \cdot {\left( {\dfrac{3}{5}} \right)^x} \cdot \ln \dfrac{3}{5} + 5 \cdot {\left( {\dfrac{4}{5}} \right)^x} \cdot \ln \dfrac{4}{5} < 0,\forall x \in \mathbb{R}\)
Do đó hàm số luôn nghịch biến trên \(\mathbb{R}\) mà \(f\left( 0 \right) = 6 > 0\), \(f\left( 2 \right) = - 22 < 0\) nên $f(0).f(2)<0$ hay phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất thuộc khoảng $(0;2)$
Tìm tích tất cả các nghiệm của phương trình \({4.3^{\log \left( {100{x^2}} \right)}} + {9.4^{\log \left( {10x} \right)}} = {13.6^{1 + \log x}}\).
ĐK: \(x > 0\).
PT \(\Leftrightarrow {4.3^{2.\log \left( {10x} \right)}} + {9.2^{2.\log \left( {10x} \right)}} = {13.6^{\log \left( {10x} \right)}}\)\( \Leftrightarrow 4.\frac{{{3^{2\log \left( {10x} \right)}}}}{{{2^{2\log \left( {10x} \right)}}}} + 9.1 = 13.\frac{{{6^{\log \left( {10x} \right)}}}}{{{4^{\log \left( {10x} \right)}}}}\) \( \Leftrightarrow 4.{\left( {\dfrac{3}{2}} \right)^{2\log \left( {10x} \right)}} - 13.{\left( {\dfrac{3}{2}} \right)^{\log \left( {10x} \right)}} + 9 = 0\)
Đặt \(t = {\left( {\dfrac{3}{2}} \right)^{\log \left( {10x} \right)}} > 0\) thì phương trình trở thành:
\(4{t^2} - 13t + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \dfrac{9}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}{\left( {\dfrac{3}{2}} \right)^{\log \left( {10x} \right)}} = 1\\{\left( {\dfrac{3}{2}} \right)^{\log \left( {10x} \right)}} = \dfrac{9}{4}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\log \left( {10x} \right) = 0\\\log \left( {10x} \right) = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{{10}}\\x = 10\end{array} \right.\).
Suy ra tích các nghiệm bằng \(1\).
Cho phương trình \({11^x} + m = {\log _{11}}\left( {x - m} \right)\) với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 205;205} \right)\) để phương trình đã cho có nghiệm?
Đáp án
Đáp án
Bước 1: Sử dụng hàm đặc trưng.
Ta có
\(\begin{array}{l}\,\,\,\,\,\,\,{11^x} + m = {\log _{11}}\left( {x - m} \right)\\ \Leftrightarrow {11^x} + x = x - m + {\log _{11}}\left( {x - m} \right)\\ \Leftrightarrow {11^x} + x = {11^{{{\log }_{11}}\left( {x - m} \right)}} + {\log _{11}}\left( {x - m} \right)\,\,\left( * \right)\end{array}\)
Xét hàm số \(f\left( t \right) = {11^t} + t \Rightarrow y' = {11^t}.\ln 11 + 1 > 0\,\,\,\forall t\). Khi đó hàm số \(y = f\left( t \right)\) đồng biến trên \(\mathbb{R}\).
Do đó \(\left( * \right) \Leftrightarrow x = {\log _{11}}\left( {x - m} \right)\) \( \Leftrightarrow {11^x} = x - m \Leftrightarrow m = x - {11^x}\).
Bước 2: Khảo sát hàm số $g(x)=x-11^x$
Xét hàm số \(g\left( x \right) = x - {11^x}\) ta có \(g'\left( x \right) = 1 - {11^x}.\ln 11 = 0 \Rightarrow x = {\log _{11}}\dfrac{1}{{\ln 11}} = {x_0}\).
Bảng biến thiên:
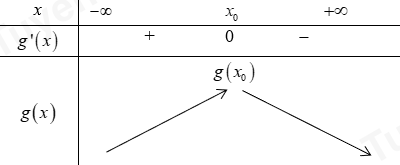
Bước 3: Biện luận nghiệm theo m.
Để phương trình đã cho có nghiệm thì \(m < g\left( {{x_0}} \right) \approx - 0,78\).
Kết hợp điều kiện đề bài ta có \(\left\{ \begin{array}{l} - 205 < m \le - 1\\m \in \mathbb{Z}\end{array} \right.\).
Vậy có 204 giá trị của nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Cho cấp số nhân có số hạng đầu tiên là 2 và công bội là 3. Số hạng thứ 2022 của cấp số đó là một số tự nhiên có bao nhiêu chữ số?
Bước 1: Tìm số hạng thứ 2022.
Ta có: số hạng thứ 2022 là: \({u_{2022}} = {u_1}.{q^{2021}} = {2.3^{2022}}\)
Bước 2: Áp dụng công thức tìm số các chữ số của số dương a là \(\left[ {\log a} \right] + 1\)
Ta có: \(\log {u_{2022}} = \log \left( {{{2.3}^{2021}}} \right)\)\( = \log 2 + \log {3^{2021}}\)\( = \log 2 + 2021.\log 3\)
Số các chữ số của \({2.3^{2021}}\) là:
\(\left[ {\log {u_{2022}}} \right] + 1\)\( = \left[ {\log 2 + 2021.\log 3} \right] + 1\)\( = 964 + 1 = 965\)
Cho cấp số nhân có số hạng đầu tiên là 2 và công bội là 3. Số hạng thứ 2022 của cấp số đó là một số tự nhiên có bao nhiêu chữ số?
Bước 1: Tìm số hạng thứ 2022.
Ta có: số hạng thứ 2022 là: \({u_{2022}} = {u_1}.{q^{2021}} = {2.3^{2022}}\)
Bước 2: Áp dụng công thức tìm số các chữ số của số dương a là \(\left[ {\log a} \right] + 1\)
Ta có: \(\log {u_{2022}} = \log \left( {{{2.3}^{2021}}} \right)\)\( = \log 2 + \log {3^{2021}}\)\( = \log 2 + 2021.\log 3\)
Số các chữ số của \({2.3^{2021}}\) là:
\(\left[ {\log {u_{2022}}} \right] + 1\)\( = \left[ {\log 2 + 2021.\log 3} \right] + 1\)\( = 964 + 1 = 965\)
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây:
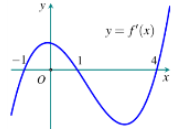
Tìm số điểm cực trị của hàm số \(y = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\)
Bước 1: Tính y'
Ta có:
\(\begin{array}{l}y = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\\y' = 2f'\left( x \right).{e^{2f\left( x \right) + 1}} + f'\left( x \right){.5^{f\left( x \right)}}.\ln 5\\ = f'\left( x \right)\left[ {2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\ln 5} \right]\end{array}\)
Bước 2: Chứng minh dấu của y' chỉ phụ thuộc vào dấu của $f'(x)$ và tìm số cực trị.
Ta thấy \(2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\ln 5 > 0\forall x\)
=> Dấu của y’ phụ thuộc vào dấu của \(f'\left( x \right)\).
Dựa vào đồ thị ta thấy \(f'\left( x \right)\) đổi dấu 3 lần nên số điểm cực trị của hàm số ban đầu là 3.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {\ln x + 1} \right)\left( {{e^x} - 2019} \right)\left( {x + 1} \right)\) trên khoảng \(\left( {0; + \infty } \right)\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Đáp án:
Đáp án:
TXĐ: \(D = \left( {0; + \infty } \right)\).
Ta có:
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\ln x + 1 = 0\\{e^x} - 2019 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\ln x = - 1\\{e^x} = 2019\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{e} \in \left( {0; + \infty } \right)\\x = \ln 2019 \in \left( {0; + \infty } \right)\\x = - 1 \notin \left( {0; + \infty } \right)\end{array} \right.\)
Vậy hàm số đã cho có 2 điểm cực trị.
Xét các số thực dương \(a\) và \(b\) thỏa mãn \({\log _3}\left( {1 + ab} \right) = \dfrac{1}{2} + {\log _3}\left( {b - a} \right)\). Giá trị nhỏ nhất của biểu thức \(P = \dfrac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}}\) bằng:
Đáp án:
Đáp án:
Bước 1: Tìm điều kiện và tìm mối quan hệ giữa a và b từ đẳng thức bài cho.
ĐKXĐ: \(\left\{ \begin{array}{l}b - a > 0\\a,\,\,b > 0\end{array} \right.\).
Ta có:
\(\begin{array}{l}{\log _3}\left( {1 + ab} \right) = \dfrac{1}{2} + {\log _3}\left( {b - a} \right)\\ \Leftrightarrow {\log _3}\left( {1 + ab} \right) - {\log _3}\left( {b - a} \right) = \dfrac{1}{2}\\ \Leftrightarrow {\log _3}\dfrac{{1 + ab}}{{b - a}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{1 + ab}}{{b - a}} = \sqrt 3 \\ \Leftrightarrow 1 + ab = \sqrt 3 \left( {b - a} \right)\\ \Leftrightarrow \dfrac{1}{a} + b = \sqrt 3 \left( {\dfrac{b}{a} - 1} \right)\end{array}\)
Bước 2: Sử dụng BĐT Cô-si để đánh giá $\dfrac{a}{b}$
Áp dụng BĐT Cô-si ta có \(\dfrac{1}{a} + b \ge 2\sqrt {\dfrac{b}{a}} \) nên
\(\sqrt 3 \left( {\dfrac{b}{a} - 1} \right) \ge 2\sqrt {\dfrac{b}{a}} \Leftrightarrow \sqrt 3 \dfrac{b}{a} - 2\sqrt {\dfrac{b}{a}} - \sqrt 3 \ge 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\sqrt {\dfrac{b}{a}} \ge \sqrt 3 \\\sqrt {\dfrac{b}{a}} \le - \dfrac{1}{{\sqrt 3 }}\,\,\left( {Loai} \right)\end{array} \right. \Leftrightarrow \sqrt {\dfrac{b}{a}} \ge \sqrt 3 \Leftrightarrow \dfrac{b}{a} \ge 3\)
Bước 3: Sử dụng BĐT Cô-si để đánh giá P.
Ta có: \(P = \dfrac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}} = \dfrac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}}\).
Áp dụng BĐT Cô-si ta có \(1 + {a^2}{b^2} \ge 2\sqrt {{a^2}{b^2}} = 2ab\) nên \(1 + {a^2} + {b^2} + {a^2}{b^2} \ge {a^2} + {b^2} + 2ab = {\left( {a + b} \right)^2}\).
\( \Rightarrow P = \dfrac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{a\left( {a + b} \right)}} = \dfrac{{a + b}}{a} = 1 + \dfrac{b}{a} \ge 4\).
Vậy \({P_{\min }} = 4 \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{a} = b\\\dfrac{b}{a} = 3\\a,\,\,b > 0,\,\,b - a > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{a} = 3a\\b = 3a\\a,\,\,b > 0,\,\,b - a > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{{\sqrt 3 }}\\b = \sqrt 3 \end{array} \right.\).
Xét các số thực \(x,y\) thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} - 2x + 2} \right){4^x}\). Giá trị lớn nhất của biểu thức \(P = \dfrac{{8x + 4}}{{2x - y + 1}}\) là $a+\sqrt{a}$
Tìm $a$
Đáp án:
Đáp án:
Bước 1: Chia cả 2 vế của bất phương trình cho $4^x$ và đặt \(t = {x^2} + {y^2} - 2x + 1\)
Nhận xét: \({x^2} + {y^2} - 2x + 2 = {\left( {x - 1} \right)^2} + {y^2} + 1 > 0\,\,\,\forall x,y\).
Bpt \( \Leftrightarrow {2^{{x^2} + {y^2} - 2x + 1}} \le {x^2} + {y^2} - 2x + 2\).
Đặt \(t = {x^2} + {y^2} - 2x + 1\), bất phương trình trở thành \({2^t} \le t + 1 \Leftrightarrow {2^t} - t - 1 \le 0\).
Bước 2: Xét hàm đặc trưng \(f\left( t \right) = {2^t} - t - 1\) và đánh giá $t$ từ đó đánh giá ${\left( {x - 1} \right)^2} + {y^2}$
Xét hàm số \(f\left( t \right) = {2^t} - t - 1\) có \(f'\left( t \right) = {2^t}\ln 2 - 1 = 0 \Leftrightarrow t = {\log _2}\left( {{{\log }_2}e} \right).\)
BBT:
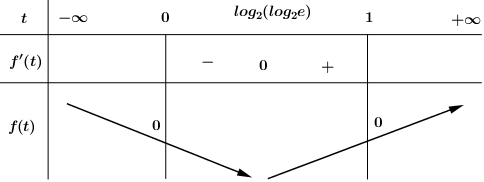
Suy ra ta có \(0 \le t \le 1 \Rightarrow {\left( {x - 1} \right)^2} + {y^2} \le 1\).
Bước 3: Biến đổi P và tìm min, max
Ta có:
\(P = \dfrac{{8x + 4}}{{2x - y + 1}}\)\( \Leftrightarrow 2Px - Py + P = 8x + 4\)
\( \Leftrightarrow P - 4 = \left( {8 - 2P} \right)x + Py\)\( \Leftrightarrow 3P - 12 = \left( {8 - 2P} \right)\left( {x - 1} \right) + Py\)
\( \Leftrightarrow {\left( {3P - 12} \right)^2} \le \left[ {{{\left( {8 - 2P} \right)}^2} + {P^2}} \right]\left[ {{{\left( {x - 1} \right)}^2} + {y^2}} \right]\)
\( \Rightarrow {\left( {3P - 12} \right)^2} \le {\left( {8 - 2P} \right)^2} + {P^2}\)\( \Leftrightarrow 4{P^2} - 40P + 80 \le 0\)
\( \Leftrightarrow 5 - \sqrt 5 \le P \le 5 + \sqrt 5\)
Bước 4: Xét dấu “=” xảy ra
Dấu “=” xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{8 - 2P}}{P} = \dfrac{{x - 1}}{y} = - \dfrac{2}{{\sqrt 5 }}}\\{{{\left( {x - 1} \right)}^2} + {y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 1 = - \dfrac{2}{{\sqrt 5 }}y}\\{\dfrac{9}{5}{y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 \mp \dfrac{2}{3}}\\{y = \pm \dfrac{{\sqrt 5 }}{3}}\end{array}} \right.\)
\( \Rightarrow \max P = 5 + \sqrt 5 \) đạt được khi \(x = \dfrac{1}{3};y = \dfrac{{\sqrt 5 }}{3}\).
Vậy $a=5$
Áp suất không khí \(P\) là một đại lượng được tính theo công thức \(P\left( x \right) = {P_0}{e^{xi}}\) trong đó \(x\) là độ cao, \({P_0} = 760{\rm{mmHg}}\) là áp suất ở mực nước biển, \(i\) là hệ số suy giảm. Biết rằng, tại độ cao \(1000\;{\rm{m}}\) thì áp suất của không khí là \(672,72{\rm{mmHg}}\). Áp suất của không khí ở độ cao \(15\;{\rm{km}}\) gần nhất với số nào trong các số sau?
122
122
122
Bước 1: Tìm hệ số suy giảm
Do ở độ cao \(1000\;{\rm{m}}\), áp suất của không khí là \(672,72{\rm{mmHg}}\) nên ta có:
\(P\left( {1000} \right) = 672,72 = 760{e^{1000i}}\)\( \Leftrightarrow i = \dfrac{1}{{1000}}\ln \dfrac{{672,72}}{{760}}\)
Bước 2: Tính \(P\left( {15000} \right)\)
Khi ở độ cao \(15\;{\rm{km}}\) tức là \(15000\;{\rm{m}}\) thì áp suất của không khí là
\(P\left( {15000} \right) = 760{e^{15000 \times \frac{1}{{1000}}\ln \frac{{672,72}}{{760}}}}\)\( \approx 121,93399\)(mmHg)
Vậy áp suất của không khí ở độ cao \(15\;{\rm{km}}\) gần nhất với số 122 .

