Câu hỏi:
2 năm trước
Với giá trị nào của $x$ để hàm số $y = {2^{2{{\log }_3}x - \log _3^2x}}$ đạt giá trị lớn nhất?
Trả lời bởi giáo viên
Đáp án đúng: b
Tập xác định của hàm số \(y = {2^{2{{\log }_3}x - \log _3^2x}}\) là \(D = \left( {0; + \infty } \right)\).
Ta có:
\(y' = {\left( {{2^{2{{\log }_3}x - \log _3^2x}}} \right)^\prime } = \left( {\dfrac{2}{{x\ln 3}} - \dfrac{{2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2 = \left( {\dfrac{{2 - 2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2\)
\(y' = 0 \Leftrightarrow \left( {\dfrac{{2 - 2{{\log }_3}x}}{{x\ln 3}}} \right){2^{2{{\log }_3}x - \log _3^2x}}.\ln 2 = 0 \) \(\Leftrightarrow {\log _3}x = 1 \Leftrightarrow x = 3\)
Bảng biến thiên:
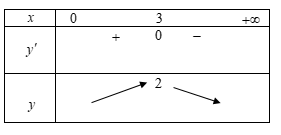
Dựa và bảng biến thiên ta có hàm số \(y = {2^{2{{\log }_3}x - \log _3^2x}}\) đạt giá trị lớn nhất bằng \(2\) tại \(x = 3\)
Hướng dẫn giải:
- Tìm ĐKXĐ.
- Khảo sát hàm số trên khoảng tìm được ở trên, lập bảng biến thiên và kết luận.
