Cho \(f(x)\) liên tục trên \(\mathbb{R}\) và \(f(2) = 16,\,\,\int\limits_0^1 {f(2x)dx = 2.} \) Tích phân \(\int\limits_0^2 {xf'\left( x \right)} dx\) bằng
Xét $\int\limits_0^1 {f\left( {2x} \right) = 2,} $ đặt \(2x = t \Leftrightarrow 2dx = dt \Leftrightarrow dx = \dfrac{{dt}}{2}\).
Đổi cận \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = 2\end{array} \right.\)
$ \Rightarrow 2 = \dfrac{1}{2}\int\limits_0^2 {f\left( t \right)dt} \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = 4.$
Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\)
$ \Rightarrow \int\limits_0^2 {x.f'\left( x \right)dx} = x.f\left( x \right)\left| \begin{array}{l}^2\\_0\end{array} \right. - \int\limits_0^2 {f\left( x \right)dx} = 2f\left( 2 \right) - 4 = 2.16 - 4 = 28.$
Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên \(\left[ {0;1} \right]\) và thỏa mãn \(f\left( 1 \right) = 0\); \(\int\limits_0^1 {{{\left[ {f'\left( x \right)} \right]}^2}dx} = \int\limits_0^1 {\left( {x + 1} \right){e^x}f\left( x \right)dx} = \dfrac{{{e^2} - 1}}{4}\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \) .
Đặt \(\left\{ \begin{array}{l}u = f\left( x \right)\\dv = \left( {x + 1} \right){e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = f'\left( x \right)dx\\v = x{e^x}\end{array} \right.\)
Khi đó \(\dfrac{{{e^2} - 1}}{4} = \left. {x.{e^x}f\left( x \right)} \right|_0^1 - \int\limits_0^1 {x.{e^x}f'\left( x \right)dx} \Rightarrow \int\limits_0^1 {x.{e^x}f'\left( x \right)dx} = - \dfrac{{{e^2} - 1}}{4}\)
Ta có: $\int\limits_0^1 {{{\left[ {f'\left( x \right) + x{e^x}} \right]}^2}dx} $$ = \int\limits_0^1 {{{\left[ {f'\left( x \right)} \right]}^2}dx} + 2\int\limits_0^1 {x.{e^x}f'\left( x \right)dx} + \int\limits_0^1 {{x^2}{e^{2x}}dx} $
\( = \dfrac{{{e^2} - 1}}{4} - 2\dfrac{{{e^2} - 1}}{4} + \dfrac{{{e^2} - 1}}{4} = 0\)
$ \Rightarrow f'\left( x \right) + x{e^x} = 0 \Rightarrow f'\left( x \right) = - x{e^x}$$ \Rightarrow f\left( x \right) = - \int {x{e^x}dx} = - \int {xd\left( {{e^x}} \right)} $$ = - \left( {x{e^x} - \int {{e^x}dx} + C} \right) = - x{e^x} + {e^x} + C$
Mà $f\left( 1 \right) = - e + e + C = 0 \Leftrightarrow C = 0$$ \Rightarrow f\left( x \right) = - x{e^x} + {e^x} = {e^x}\left( {1 - x} \right)$
Do đó
\(\begin{array}{l}\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {\left( {1 - x} \right){e^x}} dx = \int\limits_0^1 {\left( {1 - x} \right)d\left( {{e^x}} \right)} \\ = \left. {\left( {1 - x} \right){e^x}} \right|_0^1 + \int\limits_0^1 {{e^x}dx} = - 1 + e - 1 = e - 2\end{array}\)
Cho \(f\left( x \right) = \dfrac{x}{{{{\cos }^2}x}}\) trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) và \(F\left( x \right)\) là một nguyên hàm của hàm số \(xf'\left( x \right)\) thỏa mãn \(F\left( 0 \right) = 0\). Biết \(a \in \left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) thỏa mãn \(\tan a = 3\). Tính \(F\left( a \right) - 10{a^2} + 3a\).
Ta có: $F\left( x \right) = \int {xf'\left( x \right)dx} = \int {xd\left( {f\left( x \right)} \right)} $ $ = xf\left( x \right) - \int {f\left( x \right)dx} + C$
$\begin{array}{l} \Rightarrow F\left( x \right) = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - \int {\dfrac{x}{{{{\cos }^2}x}}dx} + C = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - \int {xd\left( {\tan x} \right)} + C\\F\left( x \right) = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x + \int {\tan xdx} + C = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x + \int {\dfrac{{\sin x}}{{\cos x}}dx} + C\\F\left( x \right) = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \int {\dfrac{{d\left( {\cos x} \right)}}{{\cos x}}} + C = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \ln \left| {\cos x} \right| + C\\F\left( 0 \right) = C = 0 \Rightarrow F\left( x \right) = \dfrac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \ln \left| {\cos x} \right|\\\tan a = 3 \Rightarrow \dfrac{1}{{{{\cos }^2}a}} = {\tan ^2}a + 1 = 10 \Leftrightarrow \cos a = \dfrac{1}{{\sqrt {10} }}\,\,\left( {a \in \left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)} \right)\end{array}$
$ \Rightarrow F\left( a \right) = 10{a^2} - 3a - \ln \dfrac{1}{{\sqrt {10} }}$ $ \Rightarrow F\left( a \right) - 10{a^2} + 3a$ $ = - \ln \dfrac{1}{{\sqrt {10} }} = - \dfrac{1}{2}\ln \dfrac{1}{{10}} = \dfrac{1}{2}\ln 10$
Xét hàm số $f(x)$ liên tục trên đoạn $\left[ {0;1} \right]$ và thỏa mãn điều kiện $4x.f({x^2}) + 3f(1 - x) = \sqrt {1 - {x^2}} $. Tích phân $I = \int_0^1 {f(x)dx} $ bằng
Tích phân hai vế của phương trình: $4x.f({x^2}) + 3f(1 - x) = \sqrt {1 - {x^2}} $, ta được:
$4\int\limits_0^1 {x.f({x^2})dx} + 3\int\limits_0^1 {f(1 - x)dx} = \int\limits_0^1 {\sqrt {1 - {x^2}} dx} $ (1)
Giả sử $F(x)$ là một nguyên hàm của $f(x)$.
$\int\limits_0^1 {x.f({x^2})dx} = \dfrac{1}{2}\int\limits_0^1 {f({x^2})d{x^2}} $$ = \dfrac{1}{2}\left( {F({1^2}) - F({0^2})} \right) = \dfrac{1}{2}\left( {F(1) - F(0)} \right)$
$\int\limits_0^1 {f(1 - x)dx} = - \int\limits_0^1 {f(1 - x)d\left( {1 - x} \right)} $$ = - \left( {F(1 - 1) - F(1 - 0)} \right) = - \left( {F(0) - F(1)} \right)$
$\int\limits_0^1 {\sqrt {1 - {x^2}} dx} $ là $\dfrac{1}{4}$ diện tích hình tròn tâm $O\left( {0;0} \right)$ bán kính $1$ (phương trình: ${x^2} + {y^2} \le 1$) $ \Rightarrow \int\limits_0^1 {\sqrt {1 - {x^2}} dx} = \dfrac{1}{4}.\pi .{R^2} = \dfrac{1}{4}\pi {.1^2} = \dfrac{\pi }{4}$
Khi đó, $(1) \Leftrightarrow 4.\dfrac{1}{2}.(F(1) - F(0)) - 3(F(0) - F(1)) = \dfrac{\pi }{4}$ $ \Leftrightarrow 5(F(1) - F(0)) = \dfrac{\pi }{4}$ $ \Leftrightarrow F(1) - F(0) = \dfrac{\pi }{{20}}$
$I = \int_0^1 {f(x)dx} = F(1) - F(0) = \dfrac{\pi }{{20}}$ .
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 2 \right) = - \dfrac{1}{5}\) và \(f'\left( x \right) = {x^3}{\left[ {f\left( x \right)} \right]^2}\) với mọi \(x \in R.\) Giá trị của \(f\left( 1 \right)\) bằng:
Ta có: \(f'\left( x \right) = {x^3}{\left[ {f\left( x \right)} \right]^2} \Leftrightarrow \dfrac{{f'\left( x \right)}}{{{f^2}\left( x \right)}} = {x^3}\)
\( \Rightarrow \int {\dfrac{{f'\left( x \right)}}{{{f^2}\left( x \right)}}dx = \int {{x^3}dx} \Leftrightarrow - \dfrac{1}{{f\left( x \right)}} = \dfrac{{{x^4}}}{4} + C.} \)
Theo đề bài ta có: \(f\left( 2 \right) = - \dfrac{1}{5} \Rightarrow - \dfrac{1}{{ - \dfrac{1}{5}}} = \dfrac{{{2^4}}}{4} + C \Leftrightarrow C = 1.\)
\( \Rightarrow - \dfrac{1}{{f\left( x \right)}} = \dfrac{{{x^4}}}{4} + 1 \Rightarrow - \dfrac{1}{{f\left( 1 \right)}} = \dfrac{1}{4} + 1 \Leftrightarrow f\left( 1 \right) = - \dfrac{4}{5}.\)
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + \dfrac{3}{4}\) và \(g\left( x \right) = d{x^2} + ex - \dfrac{3}{4}\;\;\left( {a,\;b,\;c,\;d \in R} \right).\) Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2;\;1;\;3\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng:
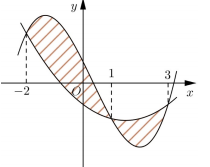
Ta có đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2;\;1;\;3\)
\( \Rightarrow \left\{ \begin{array}{l} - 8a + 4b - 2c + \dfrac{3}{4} = 4d - 2e - \dfrac{3}{4}\\a + b + c + \dfrac{3}{4} = d + e - \dfrac{3}{4}\\27a + 9b + 3c + \dfrac{3}{4} = 9d + 3e - \dfrac{3}{4}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}4a - 2b + c + 2d - e = \dfrac{3}{4}\\a + b + c - d - e = - \dfrac{3}{2}\\9a + 3b + c - 3d - e = - \dfrac{1}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}4a - 2\left( {b - d} \right) + \left( {c - e} \right) = \dfrac{3}{4}\\a + \left( {b - d} \right) + \left( {c - e} \right) = - \dfrac{3}{2}\\9a + 3\left( {b - d} \right) + \left( {c - e} \right) = - \dfrac{1}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{4}\\b - d = - \dfrac{1}{2}\\c - e = - \dfrac{5}{4}\end{array} \right..\)
Dựa vào đồ thị hình vẽ ta có:
$\begin{array}{l}S = \int\limits_{ - 2}^1 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \\ = \int\limits_{ - 2}^1 {\left( {a{x^3} + b{x^2} + cx + \dfrac{3}{4} - d{x^2} - ex + \dfrac{3}{4}} \right)dx} + \int\limits_1^3 {\left( {d{x^2} + ex - \dfrac{3}{4} - a{x^3} - b{x^2} - cx - \dfrac{3}{4}} \right)dx} \\ = \int\limits_{ - 2}^1 {\left( {a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x + \dfrac{3}{2}} \right)dx} + \int\limits_1^3 {\left( { - a{x^3} - \left( {b - d} \right){x^2} - \left( {c - e} \right)x - \dfrac{3}{2}} \right)dx} \\ = \int\limits_{ - 2}^1 {\left[ {\dfrac{1}{4}{x^3} - \dfrac{1}{2}{x^2} - \dfrac{5}{4}x + \dfrac{3}{2}} \right]dx} + \int\limits_1^3 {\left[ { - \dfrac{1}{4}{x^3} + \dfrac{1}{2}{x^2} + \dfrac{5}{4}x - \dfrac{3}{2}} \right]dx} \\ = \left. {\left[ {\dfrac{{{x^4}}}{{16}} - \dfrac{{{x^3}}}{6} - \dfrac{{5{x^2}}}{8} + \dfrac{3}{2}x} \right]} \right|_{ - 2}^1 - \left. {\left[ {\dfrac{{{x^4}}}{{16}} - \dfrac{{{x^3}}}{6} - \dfrac{{5{x^2}}}{8} + \dfrac{3}{2}x} \right]} \right|_1^3\\ = - \dfrac{{15}}{{16}} - \dfrac{3}{2} + \dfrac{{15}}{8} + \dfrac{9}{2} - \left( {5 - \dfrac{{13}}{3} - 5 + 3} \right) = \dfrac{{253}}{{48}}.\end{array}$
Một vật chuyển động trong $3$ giờ với vận tốc $v\,\,(km/h)$ phụ thuộc vào thời gian $t\,\,(h)$ có đồ thị vận tốc như hình bên. Trong khoảng thời gian $1$ giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh $I(2;5)$ và có trục đối xứng song song với trục tung, khoảng thời gian còn lại của đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong $3$ giờ đó
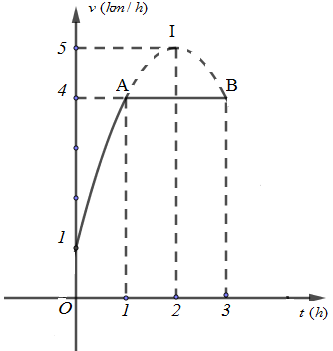
Gọi phương trình của vận tốc trong 1h đầu là: $v(t) = a\,{t^2} + bt + c\,\,(a \ne 0)$
Quan sát hình vẽ, ta thấy đồ thị hàm số có đỉnh $I(2;5)$ và đi qua điểm $A(1;4),\,\,\,(0;1)$.
Suy ra: $\left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = 5\\c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = - 4a\\4a + 2b + 1 = 5\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a = - 1\\b = 4\end{array} \right. \Rightarrow v(t) = - {t^2} + 4t + 1$
Quãng đường vật chuyển động trong 1 giờ đầu là:
$s = \int_0^1 {v(t)dt} = \int_0^1 {\left( { - {t^2} + 4t + 1} \right)dt} = \left. {\left( { - \dfrac{{{t^3}}}{3} + 2{t^2} + t} \right)} \right|_0^1 = - \dfrac{{{1^3}}}{3} + {2.1^2} + 1 - 0 = \dfrac{8}{3}\,(km)$
Trong 2h tiếp theo vật chuyển động thẳng đều với vận tốc \(4km/h\)
\( \Rightarrow \) Quãng đường đi được trong 2h tiếp theo là $8$ km.
Vậy quãng đường mà vật di chuyển được trong 3 giờ đó là: \(\dfrac{8}{3} + 8 = \dfrac{{32}}{3}\,\,\left( {km} \right)\)
Cho hàm số $y = f(x)$ liên tục và có đạo hàm trên $R$ thỏa mãn $f(2) = - 2,\,\,\int\limits_0^2 {f(x)dx} = 1$. Tính tích phân $I = \int\limits_0^4 {f'(\sqrt x )dx} $.
Tính $I = \int\limits_0^4 {f'\left( {\sqrt x } \right)dx} $:
Đặt $\sqrt x = t \Rightarrow x = {t^2} \Rightarrow dx = 2tdt$.
Đổi cận:
$\begin{array}{l}I = \int\limits_0^4 {f'(\sqrt x )dx} = \int\limits_0^2 {f'(t).2tdt} = 2\int\limits_0^2 {t.f'(t)dt} = 2\int\limits_0^2 {t.d(f(t)) = 2\left[ {t.\left. {f(t)} \right|_0^2 - \int\limits_0^2 {f\left( t \right)dt} } \right]} \\ = 2\left[ {2.f\left( 2 \right) - 0.f\left( 0 \right) - \int\limits_0^2 {f(x)dx} } \right] = 2\left[ {2.\left( { - 2} \right) - 1} \right] = - 10\end{array}$
Cho nửa đường tròn đường kính \(AB = 4\sqrt 5 \). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với $AB.$ Parabol cắt nửa đường tròn tại hai điểm cách nhau $4cm$ và khoảng cách từ hai điểm đó đến $AB$ bằng nhau và bằng $4cm.$ Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục $AB.$ Thể tích của khối tròn xoay thu được bằng:
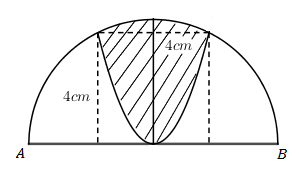
Gắn hệ trục tọa độ $Oxy$ như hình vẽ:
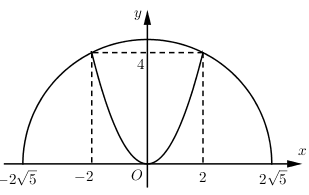
Ta có:
Phương trình đường tròn: \({x^2} + {y^2} = 20 \Rightarrow y = \sqrt {20 - {x^2}} \)
Phương trình parabol: \(y = {x^2}\)
Thể tích khối cầu \(V = \dfrac{4}{3}\pi {\left( {2\sqrt 5 } \right)^3} = \dfrac{{160\sqrt 5 }}{3}\pi \)
Thể tích khi quay phần gạch chéo quanh trục $Ox$ là: \(V' = \pi \int\limits_{ - 2}^2 {\left( {20 - {x^2} - {x^4}} \right)dx} = \dfrac{{928}}{{15}}\pi \)
\( \Rightarrow \) Thể tích cần tính \({V_1} = V - V' = \dfrac{{160\sqrt 5 }}{3}\pi - \dfrac{{928}}{{15}}\pi = \dfrac{\pi }{{15}}\left( {800\sqrt 5 - 928} \right)\)
Cho hàm số \(f\left( x \right)\) xác định trên \(R\backslash \left\{ { \pm 1} \right\}\) thỏa mãn \(f'\left( x \right) = \dfrac{1}{{{x^2} - 1}}\). Biết \(f\left( { - 3} \right) + f\left( 3 \right) = 0\) và \(f\left( { - \dfrac{1}{2}} \right) + f\left( {\dfrac{1}{2}} \right) = 2\). Giá trị \(T = f\left( { - 2} \right) + f\left( 0 \right) + f\left( 4 \right)\) bằng:
$\begin{array}{l}\,\,\,\,f\left( x \right) = \int {f'\left( x \right)dx} = \int {\dfrac{1}{{{x^2} - 1}}dx} = \dfrac{1}{2}\ln \left| {\dfrac{{x - 1}}{{x + 1}}} \right| + C\\ \Rightarrow f\left( x \right) = \left[ \begin{array}{l}\dfrac{1}{2}\ln \dfrac{{x - 1}}{{x + 1}} + {C_1}\,\,\,\,\,\,\,khi\,x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\\\dfrac{1}{2}\ln \dfrac{{1 - x}}{{x + 1}} + {C_2}\,\,\,\,\,\,\,khi\,x \in \left( { - 1;1} \right)\end{array} \right.\\ \Rightarrow f\left( { - 3} \right) + f\left( 3 \right) = \dfrac{1}{2}\ln 2 + {C_1} + \dfrac{1}{2}\ln \dfrac{1}{2} + {C_1} = 0 \Leftrightarrow {C_1} = 0\\\,\,\,\,\,\,f\left( { - \dfrac{1}{2}} \right) + f\left( {\dfrac{1}{2}} \right) = \dfrac{1}{2}\ln 3 + {C_2} + \dfrac{1}{2}\ln \dfrac{1}{3} + {C_2} = 2 \Leftrightarrow {C_2} = 1\\ \Rightarrow f\left( x \right) = \left[ \begin{array}{l}\dfrac{1}{2}\ln \dfrac{{x - 1}}{{x + 1}}\,\,\,\,\,\,\,\,\,\,\,\,khi\,x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\\\dfrac{1}{2}\ln \dfrac{{1 - x}}{{x + 1}}\, + 1\,\,\,\,\,khi\,x \in \left( { - 1;1} \right)\end{array} \right.\\ \Rightarrow f\left( { - 2} \right) + f\left( 0 \right) + f\left( 4 \right) = \dfrac{1}{2}\ln 3 + \dfrac{1}{2}\ln 1 + 1 + \dfrac{1}{2}\ln \dfrac{3}{5} = 1 + \dfrac{1}{2}\ln \dfrac{9}{5}\end{array}$
Cho \({z_1};{z_2}\) là hai số trong các số phức thỏa mãn điểu kiện \(\left| {z - 1 - 2i} \right| = \left| {z - 3 + 2i} \right|\), đồng thời \(\left| {{z_1} - {z_2}} \right| = \sqrt 5 \). Tìm giá trị nhỏ nhất của biểu thức \(H = \left| {w - {z_1}} \right| + \left| {w - {z_2}} \right|\), trong đó \(w = 1 + 3i\).
Đặt \(z = x + yi\,\,\left( {x;y \in R} \right)\) ta có:
\(\begin{array}{l}\,\,\,\,\,\left| {z - 1 - 2i} \right| = \left| {z - 3 + 2i} \right|\\ \Leftrightarrow \left| {x + yi - 1 - 2i} \right| = \left| {x + yi - 3 + 2i} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2}\\ \Leftrightarrow - 2x - 4y + 5 = - 6x + 4y + 13\\ \Leftrightarrow 4x - 8y - 8 = 0\\ \Leftrightarrow x - 2y - 2 = 0\end{array}\)
Do đó tập hợp các điểm biểu diễn số phức z thỏa điều kiện \(\left| {z - 1 - 2i} \right| = \left| {z - 3 + 2i} \right|\) là đường thẳng \(\left( d \right):\,\,x - 2y - 2 = 0\).
Gọi \(M;N\) lần lượt là các điểm biểu diễn cho số phức \({z_1};{z_2} \Rightarrow M;N \in d\) và \(MN = \sqrt 5 \). Gọi P là điểm biểu diễn cho số phức \(w = 1 + 3i \Rightarrow P\left( {1;3} \right)\).
Theo bài ra ta có: \(H = PM + PN \ge 2\sqrt {PM.PN} \)
Dấu = xảy ra \( \Rightarrow PM = PN \Leftrightarrow \Delta PMN\) cân tại P.
Gọi H là trung điểm của MN \( \Rightarrow PH \bot d \Rightarrow PH = d\left( {P;\left( d \right)} \right) = \dfrac{{\left| {1 - 6 - 2} \right|}}{{\sqrt 5 }} = \dfrac{7}{{\sqrt 5 }}\)
\(\begin{array}{l} \Rightarrow PM = PN = \sqrt {P{H^2} + \dfrac{{M{N^2}}}{4}} = \sqrt {\dfrac{{221}}{{20}}} = \dfrac{{\sqrt {4420} }}{{20}} = \dfrac{{2\sqrt {1105} }}{{20}} = \dfrac{{\sqrt {1105} }}{{10}}\\ \Rightarrow PM + PN = 2.\dfrac{{\sqrt {1105} }}{{10}} = \dfrac{{\sqrt {1105} }}{5}\end{array}\)
Vậy \({H_{\max }} = \dfrac{{\sqrt {1105} }}{5}\).
