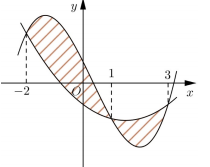
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + \dfrac{3}{4}\) và \(g\left( x \right) = d{x^2} + ex - \dfrac{3}{4}\;\;\left( {a,\;b,\;c,\;d \in R} \right).\) Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2;\;1;\;3\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng:

Ta có đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2;\;1;\;3\)

\( \Rightarrow \left\{ \begin{array}{l} - 8a + 4b - 2c + \dfrac{3}{4} = 4d - 2e - \dfrac{3}{4}\\a + b + c + \dfrac{3}{4} = d + e - \dfrac{3}{4}\\27a + 9b + 3c + \dfrac{3}{4} = 9d + 3e - \dfrac{3}{4}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}4a - 2b + c + 2d - e = \dfrac{3}{4}\\a + b + c - d - e =  - \dfrac{3}{2}\\9a + 3b + c - 3d - e =  - \dfrac{1}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}4a - 2\left( {b - d} \right) + \left( {c - e} \right) = \dfrac{3}{4}\\a + \left( {b - d} \right) + \left( {c - e} \right) =  - \dfrac{3}{2}\\9a + 3\left( {b - d} \right) + \left( {c - e} \right) =  - \dfrac{1}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{4}\\b - d =  - \dfrac{1}{2}\\c - e =  - \dfrac{5}{4}\end{array} \right..\)

Dựa vào đồ thị hình vẽ ta có:

$\begin{array}{l}S = \int\limits_{ - 2}^1 {\left| {f\left( x \right) - g\left( x \right)} \right|dx}  + \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \\ = \int\limits_{ - 2}^1 {\left( {a{x^3} + b{x^2} + cx + \dfrac{3}{4} - d{x^2} - ex + \dfrac{3}{4}} \right)dx}  + \int\limits_1^3 {\left( {d{x^2} + ex - \dfrac{3}{4} - a{x^3} - b{x^2} - cx - \dfrac{3}{4}} \right)dx} \\ = \int\limits_{ - 2}^1 {\left( {a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x + \dfrac{3}{2}} \right)dx}  + \int\limits_1^3 {\left( { - a{x^3} - \left( {b - d} \right){x^2} - \left( {c - e} \right)x - \dfrac{3}{2}} \right)dx} \\ = \int\limits_{ - 2}^1 {\left[ {\dfrac{1}{4}{x^3} - \dfrac{1}{2}{x^2} - \dfrac{5}{4}x + \dfrac{3}{2}} \right]dx}  + \int\limits_1^3 {\left[ { - \dfrac{1}{4}{x^3} + \dfrac{1}{2}{x^2} + \dfrac{5}{4}x - \dfrac{3}{2}} \right]dx} \\ = \left. {\left[ {\dfrac{{{x^4}}}{{16}} - \dfrac{{{x^3}}}{6} - \dfrac{{5{x^2}}}{8} + \dfrac{3}{2}x} \right]} \right|_{ - 2}^1 - \left. {\left[ {\dfrac{{{x^4}}}{{16}} - \dfrac{{{x^3}}}{6} - \dfrac{{5{x^2}}}{8} + \dfrac{3}{2}x} \right]} \right|_1^3\\ =  - \dfrac{{15}}{{16}} - \dfrac{3}{2} + \dfrac{{15}}{8} + \dfrac{9}{2} - \left( {5 - \dfrac{{13}}{3} - 5 + 3} \right) = \dfrac{{253}}{{48}}.\end{array}$