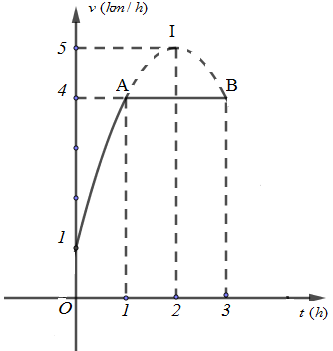
Một vật chuyển động trong $3$ giờ với vận tốc $v\,\,(km/h)$ phụ thuộc vào thời gian $t\,\,(h)$ có đồ thị vận tốc như hình bên. Trong khoảng thời gian $1$ giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh $I(2;5)$ và có trục đối xứng song song với trục tung, khoảng thời gian còn lại của đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong $3$ giờ đó

Cho \(f(x)\) liên tục trên \(\mathbb{R}\) và \(f(2) = 16,\,\,\int\limits_0^1 {f(2x)dx = 2.} \) Tích phân \(\int\limits_0^2 {xf'\left( x \right)} dx\) bằng

Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên \(\left[ {0;1} \right]\) và thỏa mãn \(f\left( 1 \right) = 0\); \(\int\limits_0^1 {{{\left[ {f'\left( x \right)} \right]}^2}dx}  = \int\limits_0^1 {\left( {x + 1} \right){e^x}f\left( x \right)dx}  = \dfrac{{{e^2} - 1}}{4}\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \) .

Cho \(f\left( x \right) = \dfrac{x}{{{{\cos }^2}x}}\) trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) và \(F\left( x \right)\) là một nguyên hàm của hàm số \(xf'\left( x \right)\) thỏa mãn \(F\left( 0 \right) = 0\). Biết \(a \in \left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) thỏa mãn \(\tan a = 3\). Tính \(F\left( a \right) - 10{a^2} + 3a\).

Xét hàm số $f(x)$ liên tục trên đoạn $\left[ {0;1} \right]$ và thỏa mãn điều kiện $4x.f({x^2}) + 3f(1 - x) = \sqrt {1 - {x^2}} $. Tích phân $I = \int_0^1 {f(x)dx} $ bằng

Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 2 \right) =  - \dfrac{1}{5}\) và \(f'\left( x \right) = {x^3}{\left[ {f\left( x \right)} \right]^2}\) với mọi \(x \in R.\) Giá trị của \(f\left( 1 \right)\) bằng:

Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + \dfrac{3}{4}\) và \(g\left( x \right) = d{x^2} + ex - \dfrac{3}{4}\;\;\left( {a,\;b,\;c,\;d \in R} \right).\) Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 2;\;1;\;3\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng: