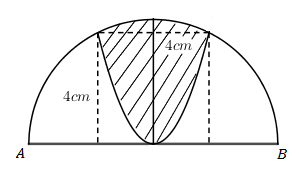
Cho nửa đường tròn đường kính \(AB = 4\sqrt 5 \). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với $AB.$ Parabol cắt nửa đường tròn tại hai điểm cách nhau $4cm$ và khoảng cách từ hai điểm đó đến $AB$ bằng nhau và bằng $4cm.$ Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục $AB.$ Thể tích của khối tròn xoay thu được bằng:
Trả lời bởi giáo viên
Gắn hệ trục tọa độ $Oxy$ như hình vẽ:
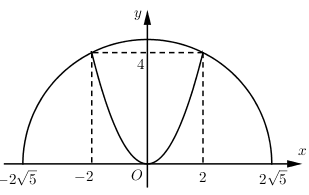
Ta có:
Phương trình đường tròn: \({x^2} + {y^2} = 20 \Rightarrow y = \sqrt {20 - {x^2}} \)
Phương trình parabol: \(y = {x^2}\)
Thể tích khối cầu \(V = \dfrac{4}{3}\pi {\left( {2\sqrt 5 } \right)^3} = \dfrac{{160\sqrt 5 }}{3}\pi \)
Thể tích khi quay phần gạch chéo quanh trục $Ox$ là: \(V' = \pi \int\limits_{ - 2}^2 {\left( {20 - {x^2} - {x^4}} \right)dx} = \dfrac{{928}}{{15}}\pi \)
\( \Rightarrow \) Thể tích cần tính \({V_1} = V - V' = \dfrac{{160\sqrt 5 }}{3}\pi - \dfrac{{928}}{{15}}\pi = \dfrac{\pi }{{15}}\left( {800\sqrt 5 - 928} \right)\)
Hướng dẫn giải:
- Tính thể tích khối cầu tâm \(O\) đường kính \(AB\)
- Tính thể tích khối tròn xoay tạo bởi khi quay phần hình phẳng giới hạn bởi nửa đường tròn với parabol quanh \(AB\)
Công thức: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
- Thể tích khối tròn xoay cần tính bằng hiệu hai thể tích vừa rồi.