Một chiếc phễu có dạng hình nón với chiều cao 30cm.Người ta đổ nước vào phễu sao cho mực nước trong phễu cao 10cm (H1). Bịt kín miệng phễu và lật ngược phễu lại (H2). Khi đó, chiều cao của mực nước trong phễu có giá trị gần nhất với?
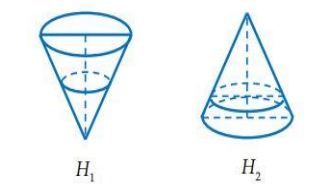
Giả sử chiếc phễu có thể tích V, bán kính đáy R, chiều cao h.
Thể tích nước đổ vào là thể tích V1 của hình nón có chiều cao \({h_1} = \dfrac{1}{3}h\), bán kính đáy \({R_1} = \dfrac{1}{3}R\).\( \Rightarrow {V_1} = {\left( {\dfrac{1}{3}} \right)^2}.\dfrac{1}{3}.V = \dfrac{1}{{27}}.V\)
Sau khi lật ngược chiếc phễu, phần không có nước là một hình nón có thể tích V2, chiều cao $h_2$
\( \Rightarrow {V_2} = \dfrac{{26}}{{27}}.V \Leftrightarrow {\left( {\dfrac{{{h_2}}}{h}} \right)^3} = \dfrac{{26}}{{27}} \Leftrightarrow {h_2} = \sqrt[3]{{\dfrac{{26}}{{27}}}}.h = \sqrt[3]{{\dfrac{{26}}{{27}}}}.30 = 29,62\left( {cm} \right)\)
Chiều cao của mực nước sau khi lật ngược là: \({h_3} = 30 - 29,62 = 0,38\left( {cm} \right)\).
Một khối đồ chơi có dạng khối nón, chiều cao bằng \(20cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng \(\dfrac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao \(h\) của lượng nước trong khối đó gần với giá trị nào sau đây?
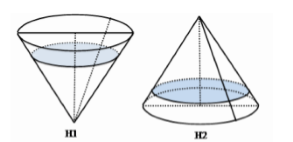
Gọi thể tích khối nón là \(V\) thì thể tích khối nước trong hình H1 là \({V_n} = {\left( {\dfrac{2}{3}} \right)^3}V\)
Thể tích phần rỗng trong hình H1 là \({V_r} = V - {V_n} = V - \dfrac{8}{{27}}V = \dfrac{{19}}{{27}}V\).
Xét hình H2, chiều cao của phần nón rỗng không có nước là \(20 - h\) (cm).
Khi đó \({V_r} = \dfrac{{19}}{{27}}V \Rightarrow {\left( {\dfrac{{20 - h}}{{20}}} \right)^3} = \dfrac{{19}}{{27}} \Leftrightarrow \dfrac{{20 - h}}{{20}} = \sqrt[3]{{\dfrac{{19}}{{27}}}} \Leftrightarrow h = 20 - 20\sqrt[3]{{\dfrac{{19}}{{27}}}} \approx 2,21\left( {cm} \right)\).
Một hình nón đỉnh \(S\) có bán kính đáy bằng \(2a\sqrt 3 \), góc ở đỉnh là \(120^\circ \). Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất \({S_{\max }}\) của thiết diện đó là bao nhiêu?
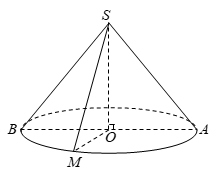
Giả sử \(O\) là tâm đáy và \(AB\) là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác cân \(SAM\). Theo giả thiết hình nón có bán kính đáy \(R = OA = 2a\sqrt 3 \), \(\widehat {ASB} = 120^\circ \) nên \(\widehat {ASO} = 60^\circ \).
Xét tam giác \(SOA\) vông tại \(O\), ta có \(\sin 60^\circ = \dfrac{{OA}}{{SA}}\)\( \Rightarrow SA = \dfrac{{OA}}{{\sin 60^\circ }} = 4a\).
Diện tích thiết diện là \({S_{SAM}} = \dfrac{1}{2}SA.SM.\sin \widehat {ASM} = \dfrac{1}{2}.4a.4a.\sin \widehat {ASM} = 8{a^2}.\sin \widehat {ASM}\)
Do \(0 < \sin \widehat {ASM} \le 1\) nên \({S_{SAM}}\) lớn nhất khi và chỉ khi \(\sin \widehat {ASM} = 1\) hay khi tam giác \(ASM\) vuông cân đỉnh \(S\) (vì \(\widehat {ASB} = 120^\circ > 90^\circ \) nên tồn tại tam giác \(ASM\) thoả mãn).
Vậy diện tích thiết diện lớn nhất là \({S_{\max }} = 8{a^2}{\mkern 1mu} \)(đvdt).
Cho khối trụ có hai đáy là hình tròn \(\left( {O;R} \right)\) và \(\left( {O';R} \right)\), \(OO' = 4R\). Trên đường tròn tâm $O$ lấy \(\left( O \right)\) lấy hai điểm $A, B$ sao cho \(AB = R\sqrt 3 \). Mặt phẳng $(P) $ đi qua $A, B$ cắt $OO’$ và tạo với đáy một góc bằng $60^0$. $(P)$ cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:
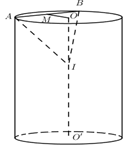
Gọi $M $ là trung điểm của $AB$ ta có:
\(OM = \sqrt {O{A^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} = \sqrt {{R^2} - \dfrac{{3{R^2}}}{4}} = \dfrac{R}{2}\)
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên \(\Delta IAB\) cân tại I, do đó \(MI \bot AB\)
Do đó góc giữa (P) và mặt đáy bằng \(\widehat {IMO} = {60^0}\)
Xét tam giác vuông IMO có : \(OI = OM.\tan 60 = \dfrac{{R\sqrt 3 }}{2} < \dfrac{{OO'}}{2} = 2R\)
\( \Rightarrow I\) nằm giữa O và O’. Do đó (P) không cắt đáy còn lại.Vậy hình chiếu của (P) trên \(\left( {O;R'} \right)\) là phần diện tích của hình quạt cung lớn AB và \(\Delta OAB\)(phần gạch chéo).
Áp dụng định lí Cosin trong tam giác OAB có :
\(\cos \widehat {AOB} = \dfrac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \dfrac{{{R^2} + {R^2} - 3{R^2}}}{{2{R^2}}} = - \dfrac{1}{2} \Rightarrow \widehat {AOB} = {120^0}\)
\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}OA.OB.\sin 120 = \dfrac{1}{2}{R^2}\dfrac{{\sqrt 3 }}{2} = {R^2}\dfrac{{\sqrt 3 }}{4}\)
Gọi ${{S}_{\overset\frown{OAB}}}$ là diện tích hình quạt $\Rightarrow {{S}_{\overset\frown{OAB}}}=\dfrac{\dfrac{4\pi }{3}}{2\pi }.\pi {{R}^{2}}=\dfrac{2}{3}\pi {{R}^{2}}$
$\Rightarrow {{S}_{hc}}={{S}_{\overset\frown{OAB}}}+{{S}_{\Delta OAB}}=\dfrac{2}{3}\pi {{R}^{2}}+{{R}^{2}}\dfrac{\sqrt{3}}{4}$
Vậy diện tích phần thiết diện cần tìm là :
${S_{hc}} = S.\cos 60 \Rightarrow S = \dfrac{{{S_{hc}}}}{{\cos 60}} = 2\left( {\dfrac{2}{3}\pi {R^2} + {R^2}\dfrac{{\sqrt 3 }}{4}} \right) = \left( {\dfrac{4}{3}\pi {R^2} + \dfrac{{\sqrt 3 }}{2}{R^2}} \right) = \left( {\dfrac{4}{3}\pi + \dfrac{{\sqrt 3 }}{2}} \right){R^2}$
Một cái phễu có dạng hình nón có chiều cao $15(cm).$ Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\dfrac{1}{3}\) chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).
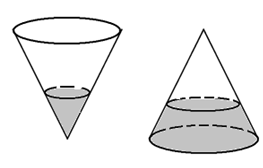
Gọi $r_1$ là bán kính đáy phễu, $r_2$ là bán kính đáy phần nước, $h_1$ và $h_2$ là chiều cao phễu và chiều cao cột nước ta có \(\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{{h_2}}}{{{h_1}}} = \dfrac{5}{{15}} = \dfrac{1}{3} \Rightarrow {r_2} = \dfrac{1}{3}{r_1}\)
Khi úp phễu xuống thì thể tích của phần nón không chứa nước là: \(\dfrac{1}{3}\pi r_1^2{h_1} - \dfrac{1}{3}\pi r_2^2{h_2} = 5\pi r_1^2 - \dfrac{5}{3}\pi {\left( {\dfrac{{{r_1}}}{3}} \right)^2} = \dfrac{{130}}{{27}}\pi r_1^2 = \dfrac{1}{3}\pi {r^2}h\) với $r, h$ là bán kính và chiều cao của hình nón không chứa nước \( \Rightarrow {r^2}h = \dfrac{{130}}{9}r_1^2\)
Ta có \(\dfrac{r}{{{r_1}}} = \dfrac{h}{{{h_1}}} \Rightarrow r = \dfrac{{{r_1}h}}{{15}} \Rightarrow \dfrac{{r_1^2{h^3}}}{{225}} = \dfrac{{130}}{9}r_1^2 \Leftrightarrow h = 14,812\,\left( {cm} \right)\)
Vậy chiều cao của nước sau khi úp phếu xuống là $15 – 14,812 = 0,188 (cm)$
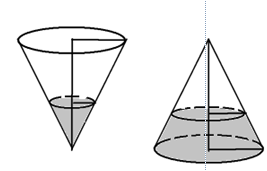
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng $10 cm$. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?

Gọi thể tích của phễu là $V,$ bán kính đáy phễu là $R,$ bán kính của cột nước có dạng khối nón trong H1 là $R_1$
Ta có: \(\dfrac{{10}}{{20}} = \dfrac{{{R_1}}}{R} = \dfrac{1}{2}\)
Gọi $V_1$ là thể tích của nước ta có:
\(\dfrac{{{V_1}}}{V} = \dfrac{{\dfrac{1}{3}\pi R_1^2.10}}{{\dfrac{1}{3}\pi{R^2}.20}} = \dfrac{1}{2}{\left( {\dfrac{{{R_1}}}{R}} \right)^2}= \dfrac{1}{8} \Rightarrow {V_1} = \dfrac{1}{8}V\)
Sau khi úp ngược phễu lên, thể tích của phần không có nước có dạng khối nón có thể tích là \({V_2} = V - {V_1} = \dfrac{7}{8}V\)
Gọi $h, R_2$ là chiều cao và bán kính đáy của khối nón không chứa nước ở H2 ta có
\(\dfrac{{{R_2}}}{R} = \dfrac{h}{{20}}\) và : \(\dfrac{{{V_2}}}{V}= \dfrac{{\dfrac{1}{3}\pi R_2^2h}}{{\dfrac{1}{3}\pi {R^2}.20}} = \dfrac{7}{8} \Rightarrow {\left( {\dfrac{{{R_2}}}{R}} \right)^2}.\dfrac{h}{{20}} =\dfrac{7}{8} \Leftrightarrow \dfrac{{{h^3}}}{{{{20}^3}}} = \dfrac{7}{8} \Rightarrow h = 10\sqrt[3]{7}\)
\( \Rightarrow \) Chiều cao của cột nước trong H2 là \(20 - 10\sqrt[3]{7}cm\) .
Cho hình tứ diện $ABCD$ có $AD \bot (ABC)$, $ABC$ là tam giác vuông tại $B.$ Biết $BC = a,$ $AB = a\sqrt 3 $, $AD = 3a.$ Quay các tam giác $ABC$ và $ABD$ (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng $AB$ ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
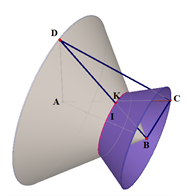
* Xét mặt phẳng (ABD):
Gọi C’ là điểm ở trong (ABD) sao cho: C’B vuông góc AB và C’B = BC = a.
Gọi $K = AC' \cap BD,\,\,IK \bot AB\,\,(I \in AB)$
Theo Ta – lét ta có:
$\dfrac{{IK}}{{BC'}} = \dfrac{{IA}}{{AB}} = 1 - \dfrac{{IB}}{{AB}} = 1 - \dfrac{{KI}}{{3BC'}} \Leftrightarrow \dfrac{4}{3}\dfrac{{KI}}{{BC'}} = 1 \Leftrightarrow \dfrac{{KI}}{{BC'}} = \dfrac{3}{4} \Rightarrow IK = \dfrac{3}{4}a$
Thể tích của phần chung là:
$V = \dfrac{1}{3}\pi I{K^2}.IA + \dfrac{1}{3}\pi I{K^2}.IB = \dfrac{1}{3}\pi I{K^2}.AB = \dfrac{1}{3}\pi .{\left( {\dfrac{{3a}}{4}} \right)^2}.a\sqrt 3 = \dfrac{{3\sqrt 3 \pi {a^3}}}{{16}}$
Có 4 viên bi hình cầu bán kính bằng 1cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc vởi cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng
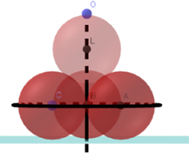
Tứ diện đều $ABCD$ có cạnh đều bằng $2$ (do $BC = BM + MC = 1 + 1 = 2$).
Tam giác $ACD$ đều, cạnh bằng $2$ => Chiều cao $AN = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 $
Tam giác $BCD $ đều, cạnh bằng $2$, $I$ là trọng tâm
=> $IN = \dfrac{1}{3}BN = \dfrac{1}{3}.\sqrt 3 = \dfrac{{\sqrt 3 }}{3}$
Tam giác $AIN$ vuông tại $I,$ theo Pytago ta có: $AI = \sqrt {A{N^2} - I{N^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} = \sqrt {\dfrac{8}{3}} = \dfrac{{\sqrt {24} }}{3} = \dfrac{{2\sqrt 6 }}{3}$
Vậy, khoảng cách từ $O $ đến mặt bàn bằng $OJ = OA + AI + IJ = 1 + $ $\dfrac{{2\sqrt 6 }}{3}$ $+ 1 = $ $\dfrac{{6 + 2\sqrt 6 }}{3}$
Cho hình chóp $S.ABCD$ có $\widehat {ABC} = \widehat {ADC} = {90^0}$, cạnh bên $SA$ vuông góc với $(ABCD)$, góc tạo bởi $SC$ và đáy $ABCD$ bằng ${60^0}$, $CD = a$ và tam giác $ADC $ có diện tích bằng $\dfrac{{{a^2}\sqrt 3 }}{2}$. Diện tích mặt cầu ngoại tiếp hình chóp $S.ABCD$ là:
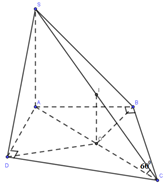
Do $\left\{ \begin{array}{l}SC \cap (ABCD) = C\\\left( {\widehat {SC,(ABCD)}} \right) = {60^0}\end{array} \right. \Rightarrow \widehat {SCA} = {60^0}$.
Tam giác ABC và tam giác ADC vuông lần lượt tại B, D, gọi O là trung điểm của AC => O là tâm đường tròn ngoại tiếp tứ giác ABCD (1)
IO là đường trung bình của tam giác SAC => IO // SA.
Mà $SA \bot (ABCD) \Rightarrow IO \bot (ABCD)$ (2)
Từ (1), (2) suy ra IA = IB = IC = ID. (3)
Do tam giác SAC vuông tại A, I là trung điểm SC $ \Rightarrow IS = IC = IA$ (4)
Từ (3), (4) suy ra I là tâm đường trong ngoại tiếp hình chóp S.ABCD.
Ta có ${S_{ACD}} = \dfrac{1}{2}AD.CD = \dfrac{1}{2}AD.a = \dfrac{{{a^2}\sqrt 3 }}{2} \Rightarrow CD = a\sqrt 3 $
Áp dụng định lý Pytago: $A{C^2} = A{D^2} + C{D^2} = {\left( {a\sqrt 3 } \right)^2} + {a^2} = 4{a^2} \Rightarrow AC = 2a.$
Tam giác SAC vuông tại A, $\widehat {SCA} = {60^0}$ $ \Rightarrow SC = \dfrac{{AC}}{{\cos C}} = \dfrac{{2a}}{{\cos {{60}^0}}} = \dfrac{{2a}}{{\dfrac{1}{2}}} = 4a$
Diện tích mặt cầu: ${S_{mc}} = 4\pi {R^2} = 4\pi {\left( {\dfrac{{SC}}{2}} \right)^2} = 4\pi {(2a)^2} = 16\pi {a^2}$
Cho hình nón ${N_1}$ có chiều cao bằng $40cm$. Người ta cắt hình nón ${N_1}$ bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ ${N_2}$ có thể tích bằng $\dfrac{1}{8}$thể tích ${N_1}$. Tính chiều cao h của hình nón ${N_2}$?
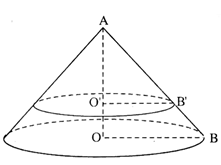
(Quan sát kí hiệu trên hình vẽ)
Áp dụng định lí Ta lét ta có:
$\dfrac{{O'B'}}{{OB}} = \dfrac{{O'A}}{{OA}} = \dfrac{{h'}}{h} = \dfrac{{h'}}{{40}}$ $(OA = h, O’A = h’< 40cm)$
Tỉ số thể tích giữa 2 khối nón:
$\begin{array}{l}\dfrac{{V'}}{V} = \dfrac{{\dfrac{1}{3}\pi .O'B{'^2}.O'A}}{{\dfrac{1}{3}\pi .O{B^2}.OA}} = \dfrac{{O'B{'^2}.O'A}}{{O{B^2}.OA}} = {\left( {\dfrac{{O'B'}}{{OB}}} \right)^2}.\dfrac{{O'A}}{{OA}} = {\left( {\dfrac{{h'}}{{40}}} \right)^2}.\dfrac{{h'}}{{40}} = \dfrac{1}{8}\\ \Rightarrow h{'^3} = \dfrac{{{{40}^3}}}{8} = {20^3} \Rightarrow h' = 20\,\,(cm)\end{array}$
Vậy chiều cao $h$ của hình nón ${N_2}$ là: $20cm.$
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều, đường cao $SH$ với $H$ nằm trong tam giác $ABC$ và $2SH = BC$, $(SBC)$ tạo với mặt phẳng $(ABC)$ một góc ${60^0}$. Biết có một điểm $O$ nằm trên đường cao $SH$ sao cho $d(O;AB) = d(O;AC) = 2d(O;(SBC)) = 1$. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
Gọi I là trung điểm của BC. Kẻ :
$\begin{array}{l}HJ \bot BC,\,\,(J \in BC);\,\,OM \bot AC,\,\,\left( {M \in AC} \right);\,\,\\ON \bot AB,\,\left( {N \in AB} \right)\,\,;\,\,OK \bot SJ,\,\left( {K \in SJ} \right)\end{array}$
Ta có: $\left\{ \begin{array}{l}HJ \bot BC\\SH \bot BC\end{array} \right. \Leftrightarrow BC \bot (SHJ) \Rightarrow BC \bot OK$
Mà $OK \bot SJ \Rightarrow OK \bot (SBC) \Rightarrow d(O,(SBC) = OK$.
Theo đề bài, ta có: $OM = ON = 2OK = 1$.
Dễ dàng chứng minh được: $\Delta OMH = \Delta ONH\,\,(ch - cgv) \Rightarrow HM = HN$
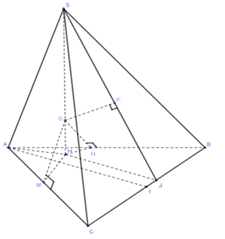
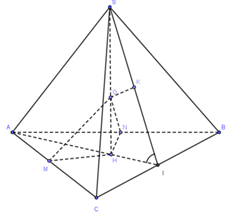
$\Delta AHM = \Delta AHN\,\,(ch - cgv) \Rightarrow \widehat {MAH} = \widehat {NAH} \Rightarrow AH$ là phân giác góc $A.$
Do $I$ là trung điểm của $BC$, tam giác $ABC$ đều
$ \Rightarrow AI$ là phân giác góc $A.$
Suy ra $A, H, I$ thẳng hàng $H \in $ đoạn thẳng $AI$ (do $H$ nằm trong tam giác $ABC$)
Ta có:
$\begin{array}{l}\left\{ \begin{array}{l}AI \bot BC\\SH \bot BC\end{array} \right. \Rightarrow BC \bot (SAI)\\ \Rightarrow \left( {\widehat {(SBC),(ABC)}} \right) = \left( {\widehat {SI,AI}} \right) = \widehat {SIA} = {60^0}\end{array}$
Tam giác $SHI$ vuông tại $H$ $ \Rightarrow \dfrac{{SH}}{{HI}} = \tan {60^0} \Rightarrow SH = \sqrt 3 HI$
Tam giác AIC vuông tại I $ \Rightarrow \dfrac{{AI}}{{IC}} = \tan {60^0} \Rightarrow AI = \sqrt 3 IC = \sqrt 3 .\dfrac{{BC}}{2} = \sqrt 3 SH$
$ \Rightarrow AI = 3HI \Rightarrow H$là trọng tâm tam giác đều ABC \( \Rightarrow M,N\) lần lượt là trung điểm của AC, AB.
$ \Rightarrow S.ABC$ là hình chóp đều. Mà $O \in SH$$ \Rightarrow OM = ON = OI = 1$
Tam giác $IOK$ vuông tại $K$: $\dfrac{{OK}}{{OI}} = \dfrac{{\dfrac{1}{2}}}{1} = \dfrac{1}{2} = \sin \widehat {KIO} \Rightarrow \widehat {KIO} = {30^0} \Rightarrow \widehat {HIO} = {60^0} - {30^0} = {30^0}$
Tam giác $HIO$ vuông tại $H$: $HI = OI.\cos {30^0} = \dfrac{{\sqrt 3 }}{2}$
Tam giác $SHI $ vuông tại $H$: $SH = HI.\tan {60^0} = \dfrac{{\sqrt 3 }}{2}.\sqrt 3 = \dfrac{3}{2} = h,\,\,\,SI = \dfrac{{HI}}{{\cos {{60}^0}}} = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}} = \sqrt 3 $
Tam giác SCI vuông tại I: $SC = \sqrt {S{I^2} + I{C^2}} = \sqrt {S{I^2} + S{H^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2}} = \dfrac{{\sqrt {21} }}{2} = a$
Bán kính mặt cầu ngoại tiếp khối chóp $S.ABC$ là: $R = \dfrac{{{a^2}}}{{2h}} = \dfrac{{{{\left( {\dfrac{{\sqrt {21} }}{2}} \right)}^2}}}{{2.\dfrac{3}{2}}} = \dfrac{{\dfrac{{21}}{4}}}{3} = \dfrac{7}{4}$
Thể tích mặt cầu ngoại tiếp khối chóp $S.ABC$ là: $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{7}{4}} \right)^3} = \dfrac{{343\pi }}{{48}}$.
Cho hình trụ có chiều cao \(h = a\sqrt 3 \), bán kính đáy \(r = a\). Gọi \(O,O'\) lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm $A, B$ sao cho hai dường thẳng $AB$ và $OO’$ chéo nhau và góc giữa hai đường thẳng $AB$ với $OO’ $ bằng $30^0$. Khoảng cách giữa hai đường thẳng $AB$ và $OO’$ bằng :
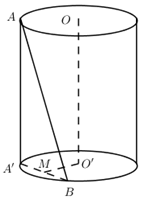
Dựng $AA'//OO'$ ta có : \(\widehat {\left( {OO';AB} \right)} = \widehat {\left( {AA';AB} \right)} = \widehat {A'AB} = {30^0}\)
Gọi $M$ là trung điểm của $A’B$ ta có:
\(\left\{ \begin{array}{l}O'M \bot A'B\\O'M \bot AA'\end{array} \right. \Rightarrow O'M \bot \left( {ABA'} \right) \Rightarrow O'M = d\left( {O';\left( {ABA'} \right)} \right)\)
\(\begin{array}{l}OO'//AA' \Rightarrow OO'//\left( {ABA'} \right) \supset AB \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {ABA'} \right)} \right)\\ = d\left( {O'\left( {ABA'} \right)} \right) = O'M\end{array}\)
Xét tam giác vuông $ABA’$ có \(A'B = AA'.\tan 30 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a\)
\( \Rightarrow MB = \dfrac{a}{2}\)
Xét tam giác vuông $O’MB$ có \(O'M = \sqrt {O'{B^2} - M{B^2}} = \dfrac{{a\sqrt 3 }}{2}\)
Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng $1, 2, 4.$ Tổng độ dài đường kính của hai quả bóng đó.
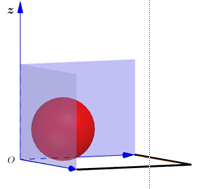
Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục $Oxyz$ như hình vẽ bên (tương tự với góc tường còn lại).
Gọi $I\left( {a;a;a} \right)$ là tâm của mặt cầu (tâm quả bóng) và $R = a.$
$ \Rightarrow $ phương trình mặt cầu của quả bóng là
$\left( S \right):{\left( {x - a} \right)^2} + {\left( {y - a} \right)^2} + {\left( {z - a} \right)^2} = {a^2}\,\,\,\,\,\,\,\,\,\,\left( 1 \right).$
Giả sử $M\left( {x;y;z} \right)$ nằm trên mặt cầu (bề mặt của quả bóng) sao cho $d\left( {M;\left( {Oxy} \right)} \right) = 1,\,\,d\left( {M;\left( {Oyz} \right)} \right) = 2,\,\,d\left( {M;\left( {Oxz} \right)} \right) = 3$
Khi đó $z = 1;\,\,x = 2;\,\,y = 3\,\, \Rightarrow \,\,M\left( {2;3;1} \right) \in \left( S \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$
Từ $\left( 1 \right),\left( 2 \right)$ suy ra ${\left( {1 - a} \right)^2} + {\left( {2 - a} \right)^2} + {\left( {4 - a} \right)^2} = {a^2}$
$ \Rightarrow \,\,\left\{ \begin{array}{l}{R_1} = {a_1} = \dfrac{{7 - \sqrt 7 }}{2}\\{R_2} = {a_2} = \dfrac{{7 + \sqrt 7 }}{2}\end{array} \right. \Rightarrow \,\,{d_1} + {d_2} = 2\left( {{R_1} + {R_2}} \right) = 14.$
Tháp nước Hàng Đậu là một di tích kiến trúc cổ của Thủ đô Hà Nội, được xây dựng vào cuối thế kỉ XIX. Tháp được thiết kế gồm thân tháp có dạng hình trụ và phần mái phía trên dạng hình nón. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ và đường kính đáy của hình nón đều bằng 19 m, chiều cao hình trụ 20 m, chiều cao hình nón là 5 m.
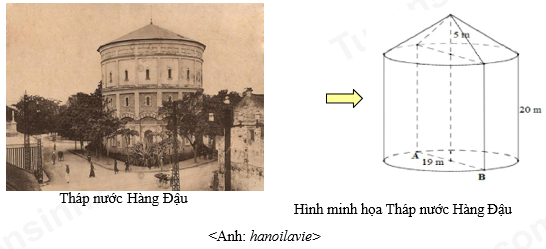
Thể tích của toàn bộ không gian bên trong tháp nước Hàng Đậu gần nhất với giá trị nào sau đây?
Bán kính đáy của hình trụ và hình nón là \(R = \dfrac{{19}}{2}\,\,\left( m \right)\).
Thể tích khối nón là
\({V_1} = \dfrac{1}{3}\pi {R^2}.{h_1} = \dfrac{1}{3}\pi .{\left( {\dfrac{{19}}{2}} \right)^2}.5\)\( = \dfrac{{1805}}{{12}}\,\,\left( {{m^3}} \right)\)
Thể tích khối trụ là
\({V_2} = \pi {R^2}{h_2} = \pi .{\left( {\dfrac{{19}}{2}} \right)^2}.20 \)\(= 1805\pi \,\,\left( {{m^3}} \right)\)
Vậy thể tích toàn bộ không gian bên trong tháp nước Hàng Đậu là \(V = {V_1} + {V_2} = \dfrac{{23465}}{{12}}\pi \approx 6143\,{m^3}\).

