Câu hỏi:
2 năm trước
Tháp nước Hàng Đậu là một di tích kiến trúc cổ của Thủ đô Hà Nội, được xây dựng vào cuối thế kỉ XIX. Tháp được thiết kế gồm thân tháp có dạng hình trụ và phần mái phía trên dạng hình nón. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ và đường kính đáy của hình nón đều bằng 19 m, chiều cao hình trụ 20 m, chiều cao hình nón là 5 m.
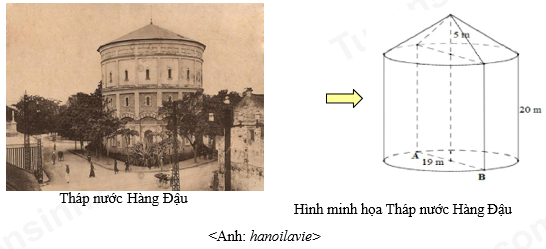
Thể tích của toàn bộ không gian bên trong tháp nước Hàng Đậu gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
Bán kính đáy của hình trụ và hình nón là \(R = \dfrac{{19}}{2}\,\,\left( m \right)\).
Thể tích khối nón là
\({V_1} = \dfrac{1}{3}\pi {R^2}.{h_1} = \dfrac{1}{3}\pi .{\left( {\dfrac{{19}}{2}} \right)^2}.5\)\( = \dfrac{{1805}}{{12}}\,\,\left( {{m^3}} \right)\)
Thể tích khối trụ là
\({V_2} = \pi {R^2}{h_2} = \pi .{\left( {\dfrac{{19}}{2}} \right)^2}.20 \)\(= 1805\pi \,\,\left( {{m^3}} \right)\)
Vậy thể tích toàn bộ không gian bên trong tháp nước Hàng Đậu là \(V = {V_1} + {V_2} = \dfrac{{23465}}{{12}}\pi \approx 6143\,{m^3}\).
Hướng dẫn giải:
- Tìm bán kính đáy của hình trụ và hình nón.
- Tính thể tích khối nón \({V_1}\) và khối trụ \({V_2}\).
- Thể tích toàn bộ không gian bên trong tháp nước Hàng Đậu là \(V = {V_1} + {V_2}\).
