Câu hỏi:
1 năm trước
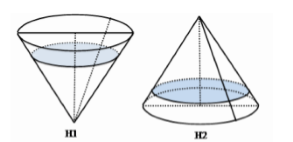
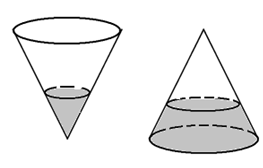
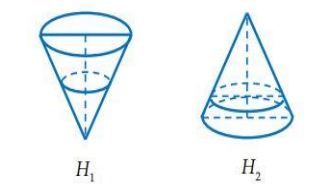
Một chiếc phễu có dạng hình nón với chiều cao 30cm.Người ta đổ nước vào phễu sao cho mực nước trong phễu cao 10cm (H1). Bịt kín miệng phễu và lật ngược phễu lại (H2). Khi đó, chiều cao của mực nước trong phễu có giá trị gần nhất với?
Trả lời bởi giáo viên
Đáp án đúng: d
Giả sử chiếc phễu có thể tích V, bán kính đáy R, chiều cao h.
Thể tích nước đổ vào là thể tích V1 của hình nón có chiều cao \({h_1} = \dfrac{1}{3}h\), bán kính đáy \({R_1} = \dfrac{1}{3}R\).\( \Rightarrow {V_1} = {\left( {\dfrac{1}{3}} \right)^2}.\dfrac{1}{3}.V = \dfrac{1}{{27}}.V\)
Sau khi lật ngược chiếc phễu, phần không có nước là một hình nón có thể tích V2, chiều cao $h_2$
\( \Rightarrow {V_2} = \dfrac{{26}}{{27}}.V \Leftrightarrow {\left( {\dfrac{{{h_2}}}{h}} \right)^3} = \dfrac{{26}}{{27}} \Leftrightarrow {h_2} = \sqrt[3]{{\dfrac{{26}}{{27}}}}.h = \sqrt[3]{{\dfrac{{26}}{{27}}}}.30 = 29,62\left( {cm} \right)\)
Chiều cao của mực nước sau khi lật ngược là: \({h_3} = 30 - 29,62 = 0,38\left( {cm} \right)\).
Hướng dẫn giải:
Quy về công thức tính thể tích hình nón.
Tính thể tích phần rỗng và suy ra tỉ số chiều cao.
