Câu hỏi:
2 năm trước
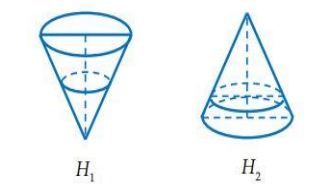
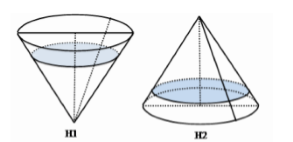
Một khối đồ chơi có dạng khối nón, chiều cao bằng \(20cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng \(\dfrac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao \(h\) của lượng nước trong khối đó gần với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
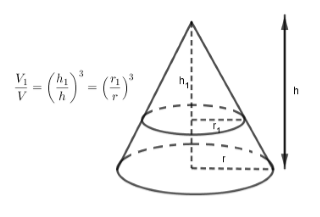
Gọi thể tích khối nón là \(V\) thì thể tích khối nước trong hình H1 là \({V_n} = {\left( {\dfrac{2}{3}} \right)^3}V\)
Thể tích phần rỗng trong hình H1 là \({V_r} = V - {V_n} = V - \dfrac{8}{{27}}V = \dfrac{{19}}{{27}}V\).
Xét hình H2, chiều cao của phần nón rỗng không có nước là \(20 - h\) (cm).
Khi đó \({V_r} = \dfrac{{19}}{{27}}V \Rightarrow {\left( {\dfrac{{20 - h}}{{20}}} \right)^3} = \dfrac{{19}}{{27}} \Leftrightarrow \dfrac{{20 - h}}{{20}} = \sqrt[3]{{\dfrac{{19}}{{27}}}} \Leftrightarrow h = 20 - 20\sqrt[3]{{\dfrac{{19}}{{27}}}} \approx 2,21\left( {cm} \right)\).
Hướng dẫn giải:
Sử dụng công thức tính thể tích hai khối nón cùng đỉnh:
