Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều, đường cao $SH$ với $H$ nằm trong tam giác $ABC$ và $2SH = BC$, $(SBC)$ tạo với mặt phẳng $(ABC)$ một góc ${60^0}$. Biết có một điểm $O$ nằm trên đường cao $SH$ sao cho $d(O;AB) = d(O;AC) = 2d(O;(SBC)) = 1$. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

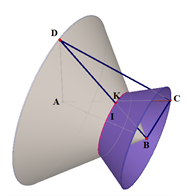
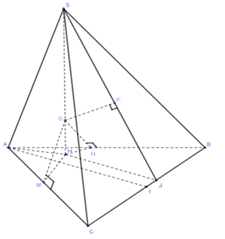
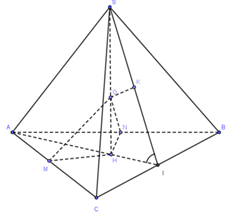
Gọi I là trung điểm của BC. Kẻ :

$\begin{array}{l}HJ \bot BC,\,\,(J \in BC);\,\,OM \bot AC,\,\,\left( {M \in AC} \right);\,\,\\ON \bot AB,\,\left( {N \in AB} \right)\,\,;\,\,OK \bot SJ,\,\left( {K \in SJ} \right)\end{array}$

Ta có: $\left\{ \begin{array}{l}HJ \bot BC\\SH \bot BC\end{array} \right. \Leftrightarrow BC \bot (SHJ) \Rightarrow BC \bot OK$

Mà $OK \bot SJ \Rightarrow OK \bot (SBC) \Rightarrow d(O,(SBC) = OK$.

Theo đề bài, ta có: $OM = ON = 2OK = 1$.

Dễ dàng chứng minh được: $\Delta OMH = \Delta ONH\,\,(ch - cgv) \Rightarrow HM = HN$

$\Delta AHM = \Delta AHN\,\,(ch - cgv) \Rightarrow \widehat {MAH} = \widehat {NAH} \Rightarrow AH$ là phân giác góc $A.$

Do $I$ là trung điểm của $BC$, tam giác $ABC$ đều

$ \Rightarrow AI$ là phân giác góc $A.$

Suy ra $A, H, I$ thẳng hàng $H \in $ đoạn thẳng $AI$ (do $H$ nằm trong tam giác $ABC$)

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}AI \bot BC\\SH \bot BC\end{array} \right. \Rightarrow BC \bot (SAI)\\ \Rightarrow \left( {\widehat {(SBC),(ABC)}} \right) = \left( {\widehat {SI,AI}} \right) = \widehat {SIA} = {60^0}\end{array}$

Tam giác $SHI$ vuông tại $H$ $ \Rightarrow \dfrac{{SH}}{{HI}} = \tan {60^0} \Rightarrow SH = \sqrt 3 HI$

Tam giác AIC vuông tại I $ \Rightarrow \dfrac{{AI}}{{IC}} = \tan {60^0} \Rightarrow AI = \sqrt 3 IC = \sqrt 3 .\dfrac{{BC}}{2} = \sqrt 3 SH$

$ \Rightarrow AI = 3HI \Rightarrow H$là trọng tâm tam giác đều ABC \( \Rightarrow M,N\) lần lượt là trung điểm của AC, AB.

$ \Rightarrow S.ABC$ là hình chóp đều. Mà $O \in SH$$ \Rightarrow OM = ON = OI = 1$

Tam giác $IOK$ vuông tại $K$:  $\dfrac{{OK}}{{OI}} = \dfrac{{\dfrac{1}{2}}}{1} = \dfrac{1}{2} = \sin \widehat {KIO} \Rightarrow \widehat {KIO} = {30^0} \Rightarrow \widehat {HIO} = {60^0} - {30^0} = {30^0}$

Tam giác $HIO$ vuông tại $H$:  $HI = OI.\cos {30^0} = \dfrac{{\sqrt 3 }}{2}$

Tam giác $SHI $ vuông tại $H$: $SH = HI.\tan {60^0} = \dfrac{{\sqrt 3 }}{2}.\sqrt 3  = \dfrac{3}{2} = h,\,\,\,SI = \dfrac{{HI}}{{\cos {{60}^0}}} = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}} = \sqrt 3 $

Tam giác SCI vuông tại I: $SC = \sqrt {S{I^2} + I{C^2}}  = \sqrt {S{I^2} + S{H^2}}  = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2}}  = \dfrac{{\sqrt {21} }}{2} = a$

Bán kính mặt cầu ngoại tiếp khối chóp $S.ABC$ là:  $R = \dfrac{{{a^2}}}{{2h}} = \dfrac{{{{\left( {\dfrac{{\sqrt {21} }}{2}} \right)}^2}}}{{2.\dfrac{3}{2}}} = \dfrac{{\dfrac{{21}}{4}}}{3} = \dfrac{7}{4}$

Thể tích mặt cầu ngoại tiếp khối chóp $S.ABC$ là:  $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{7}{4}} \right)^3} = \dfrac{{343\pi }}{{48}}$.