Câu hỏi:
2 năm trước
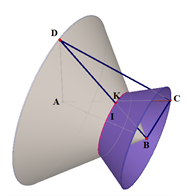
Cho hình chóp $S.ABCD$ có $\widehat {ABC} = \widehat {ADC} = {90^0}$, cạnh bên $SA$ vuông góc với $(ABCD)$, góc tạo bởi $SC$ và đáy $ABCD$ bằng ${60^0}$, $CD = a$ và tam giác $ADC $ có diện tích bằng $\dfrac{{{a^2}\sqrt 3 }}{2}$. Diện tích mặt cầu ngoại tiếp hình chóp $S.ABCD$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
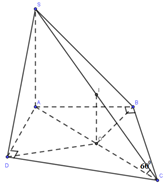
Do $\left\{ \begin{array}{l}SC \cap (ABCD) = C\\\left( {\widehat {SC,(ABCD)}} \right) = {60^0}\end{array} \right. \Rightarrow \widehat {SCA} = {60^0}$.
Tam giác ABC và tam giác ADC vuông lần lượt tại B, D, gọi O là trung điểm của AC => O là tâm đường tròn ngoại tiếp tứ giác ABCD (1)
IO là đường trung bình của tam giác SAC => IO // SA.
Mà $SA \bot (ABCD) \Rightarrow IO \bot (ABCD)$ (2)
Từ (1), (2) suy ra IA = IB = IC = ID. (3)
Do tam giác SAC vuông tại A, I là trung điểm SC $ \Rightarrow IS = IC = IA$ (4)
Từ (3), (4) suy ra I là tâm đường trong ngoại tiếp hình chóp S.ABCD.
Ta có ${S_{ACD}} = \dfrac{1}{2}AD.CD = \dfrac{1}{2}AD.a = \dfrac{{{a^2}\sqrt 3 }}{2} \Rightarrow CD = a\sqrt 3 $
Áp dụng định lý Pytago: $A{C^2} = A{D^2} + C{D^2} = {\left( {a\sqrt 3 } \right)^2} + {a^2} = 4{a^2} \Rightarrow AC = 2a.$
Tam giác SAC vuông tại A, $\widehat {SCA} = {60^0}$ $ \Rightarrow SC = \dfrac{{AC}}{{\cos C}} = \dfrac{{2a}}{{\cos {{60}^0}}} = \dfrac{{2a}}{{\dfrac{1}{2}}} = 4a$
Diện tích mặt cầu: ${S_{mc}} = 4\pi {R^2} = 4\pi {\left( {\dfrac{{SC}}{2}} \right)^2} = 4\pi {(2a)^2} = 16\pi {a^2}$
Hướng dẫn giải:
Gọi O, I lần lượt là trung điểm của AC, SC.
Do tam giác ABC và tam giác ADC vuông lần lượt tại B, D nên tâm đường tròn ngoại tiếp tứ giác ABCD là O.
Dễ dàng chứng minh được I là tâm đường tròn ngoại tiếp hình chóp S.ABCD.
Ta xác định độ dài bán kính mặt cầu ngoại tiếp hình chóp SABCD và thay vào công thức tính diện tích mặt cầu:${S_{mc}} = 4\pi {R^2}$
