Câu hỏi:
2 năm trước
Cho hình nón ${N_1}$ có chiều cao bằng $40cm$. Người ta cắt hình nón ${N_1}$ bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ ${N_2}$ có thể tích bằng $\dfrac{1}{8}$thể tích ${N_1}$. Tính chiều cao h của hình nón ${N_2}$?
Trả lời bởi giáo viên
Đáp án đúng: a
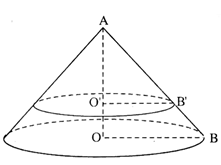
(Quan sát kí hiệu trên hình vẽ)
Áp dụng định lí Ta lét ta có:
$\dfrac{{O'B'}}{{OB}} = \dfrac{{O'A}}{{OA}} = \dfrac{{h'}}{h} = \dfrac{{h'}}{{40}}$ $(OA = h, O’A = h’< 40cm)$
Tỉ số thể tích giữa 2 khối nón:
$\begin{array}{l}\dfrac{{V'}}{V} = \dfrac{{\dfrac{1}{3}\pi .O'B{'^2}.O'A}}{{\dfrac{1}{3}\pi .O{B^2}.OA}} = \dfrac{{O'B{'^2}.O'A}}{{O{B^2}.OA}} = {\left( {\dfrac{{O'B'}}{{OB}}} \right)^2}.\dfrac{{O'A}}{{OA}} = {\left( {\dfrac{{h'}}{{40}}} \right)^2}.\dfrac{{h'}}{{40}} = \dfrac{1}{8}\\ \Rightarrow h{'^3} = \dfrac{{{{40}^3}}}{8} = {20^3} \Rightarrow h' = 20\,\,(cm)\end{array}$
Vậy chiều cao $h$ của hình nón ${N_2}$ là: $20cm.$
Hướng dẫn giải:
Công thức thể tích khối nón: ${V} = \dfrac{1}{3}\pi {R^2}h$.
Sử dụng tỉ số thể tích của hai khối nón.
