Câu hỏi:
2 năm trước
Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng $1, 2, 4.$ Tổng độ dài đường kính của hai quả bóng đó.
Trả lời bởi giáo viên
Đáp án đúng: b
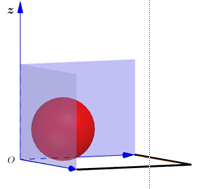
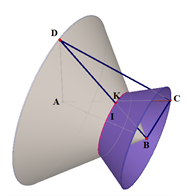
Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục $Oxyz$ như hình vẽ bên (tương tự với góc tường còn lại).
Gọi $I\left( {a;a;a} \right)$ là tâm của mặt cầu (tâm quả bóng) và $R = a.$
$ \Rightarrow $ phương trình mặt cầu của quả bóng là
$\left( S \right):{\left( {x - a} \right)^2} + {\left( {y - a} \right)^2} + {\left( {z - a} \right)^2} = {a^2}\,\,\,\,\,\,\,\,\,\,\left( 1 \right).$
Giả sử $M\left( {x;y;z} \right)$ nằm trên mặt cầu (bề mặt của quả bóng) sao cho $d\left( {M;\left( {Oxy} \right)} \right) = 1,\,\,d\left( {M;\left( {Oyz} \right)} \right) = 2,\,\,d\left( {M;\left( {Oxz} \right)} \right) = 3$
Khi đó $z = 1;\,\,x = 2;\,\,y = 3\,\, \Rightarrow \,\,M\left( {2;3;1} \right) \in \left( S \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$
Từ $\left( 1 \right),\left( 2 \right)$ suy ra ${\left( {1 - a} \right)^2} + {\left( {2 - a} \right)^2} + {\left( {4 - a} \right)^2} = {a^2}$
$ \Rightarrow \,\,\left\{ \begin{array}{l}{R_1} = {a_1} = \dfrac{{7 - \sqrt 7 }}{2}\\{R_2} = {a_2} = \dfrac{{7 + \sqrt 7 }}{2}\end{array} \right. \Rightarrow \,\,{d_1} + {d_2} = 2\left( {{R_1} + {R_2}} \right) = 14.$
Hướng dẫn giải:
Gắn hệ tọa độ $Oxyz,$ tìm bán kính quả bóng chính là bán kính của mặt cầu.
(Chỉ áp dụng khi HS đã học chương tọa độ trong không gian).
