Câu hỏi:
2 năm trước
Cho hình trụ có chiều cao \(h = a\sqrt 3 \), bán kính đáy \(r = a\). Gọi \(O,O'\) lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm $A, B$ sao cho hai dường thẳng $AB$ và $OO’$ chéo nhau và góc giữa hai đường thẳng $AB$ với $OO’ $ bằng $30^0$. Khoảng cách giữa hai đường thẳng $AB$ và $OO’$ bằng :
Trả lời bởi giáo viên
Đáp án đúng: d
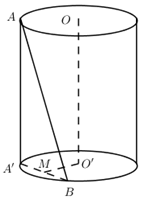
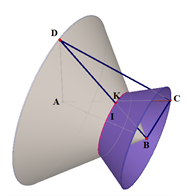
Dựng $AA'//OO'$ ta có : \(\widehat {\left( {OO';AB} \right)} = \widehat {\left( {AA';AB} \right)} = \widehat {A'AB} = {30^0}\)
Gọi $M$ là trung điểm của $A’B$ ta có:
\(\left\{ \begin{array}{l}O'M \bot A'B\\O'M \bot AA'\end{array} \right. \Rightarrow O'M \bot \left( {ABA'} \right) \Rightarrow O'M = d\left( {O';\left( {ABA'} \right)} \right)\)
\(\begin{array}{l}OO'//AA' \Rightarrow OO'//\left( {ABA'} \right) \supset AB \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {ABA'} \right)} \right)\\ = d\left( {O'\left( {ABA'} \right)} \right) = O'M\end{array}\)
Xét tam giác vuông $ABA’$ có \(A'B = AA'.\tan 30 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a\)
\( \Rightarrow MB = \dfrac{a}{2}\)
Xét tam giác vuông $O’MB$ có \(O'M = \sqrt {O'{B^2} - M{B^2}} = \dfrac{{a\sqrt 3 }}{2}\)
Hướng dẫn giải:
+) Xác định mặt phẳng $(P)$ chứa $AB$ và song song với $OO’.$
+) \(d\left( {OO';AB} \right) = d\left( {OO';\left( P \right)} \right)\)
