Trong không gian với hệ tọa độ $Oxyz,$ cho hai đường thẳng $d:\dfrac{{x + 2}}{2} = \dfrac{{y + 3}}{5} = \dfrac{{z - 4}}{{ - \,1}}$ và $d':\left\{ \begin{array}{l}x = 3 - t\\y = 1\\z = 10 + t\end{array} \right..$ Hai điểm $A \in d$ và $B \in d'$ thỏa mãn đường thẳng $AB$ vuông góc với cả hai đường thẳng $d,\,\,d'.$ Có bao nhiêu mặt cầu tiếp xúc với đường thẳng $d$ tại $A$ và tiếp xúc với đường thẳng $d'$ tại $B$ ?
Gọi $I$ là tâm mặt cầu cần tìm $ \Rightarrow $$d\left( {I;\left( d \right)} \right) = IA$ và $d\left( {I;\left( {d'} \right)} \right) = IB.$
Mà $AB$ là đoạn vuông góc chung của $d$ và $d'$$ \Rightarrow \,\,I$ là trung điểm của $AB.$
Trong không gian tọa độ Oxyz, cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 2x - 2y + 4z - 20 = 0\) và mặt phẳng \(\left( P \right):\,\,x + y - z - m = 0\). Tìm m để \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là một đường tròn có bán kính lớn nhất.
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;1; - 2} \right)\).
Ta có \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {1 + 1 - \left( { - 2} \right) - m} \right|}}{{\sqrt 3 }} = \dfrac{{\left| {4 - m} \right|}}{{\sqrt 3 }} \ge 0 \Leftrightarrow d{\left( {I;\left( P \right)} \right)_{\min }} = 0 \Leftrightarrow m = 4\).
Trong không gian với hệ tọa độ \(Oxyz\), gọi \(I\left( {a,b,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1; - 1;4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c\).
Giả sử $B\left( {a;b;0} \right)$ là hình chiếu của $I$ trên mặt phẳng $\left( {Oxy} \right)$.
Có : \(\overrightarrow {IA} = \left( {1 - a;\; - 1 - b;\;4 - c} \right);\;\;\overrightarrow {IB} = \left( {0;\;0;\;c} \right).\)
Theo bài ra, ta có $IA = IB \Leftrightarrow \,\,{\left( {a - 1} \right)^2} + {\left( {b + 1} \right)^2} + {\left( {c - 4} \right)^2} = {c^2}$ $\left( 1 \right).$
Mặt khác, mặt cầu tiếp xúc với các mặt phẳng tọa độ $ \Rightarrow \,\,\left| a \right| = \left| b \right| = \left| c \right|$ $\left( 2 \right).$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $a = 3;\,\,b = - \,3;\,\,c = 3.$
Vậy $P = a - b + c = 9.$
Trong không gian với hệ tọa độ \(Oxyz,\) cho ba điểm \(A\left( { - 1;\,0;\,1} \right)\), \(B\left( {3;\,2;\,1} \right)\), \(C\left( {5;\,3;\,7} \right)\). Gọi \(M\left( {a;\,b;\,c} \right)\) thỏa mãn \(MA = MB\) và \(MB + MC\) đạt giá trị nhỏ nhất. Tính \(P = a + b + c.\)
Ta có \(MA = MB \Rightarrow M\) thuộc mặt phẳng trung trực của đoạn thẳng \(AB\).
Gọi \(\left( P \right)\) là mặt phẳng trung trực của \(AB \Rightarrow \left( P \right):2x + y - 3 = 0\).
Lại có \(A\) và \(C\) nằm hai phía của mặt phẳng \(\left( P \right)\)
Do đó \(MB + MC = MA + MC \ge AC\).
Suy ra \(\min \left( {MB + MC} \right) = AC\) khi \(M = \left( P \right) \cap AC \Rightarrow M\left( {1;\,1;\,3} \right)\).
Trong không gian với hệ tọa độ Oxyz cho ba mặt phẳng \(\left( P \right):\,\,x - 2y + z - 1 = 0\), \(\left( Q \right):\,\,x - 2y + z + 8 = 0\) và \(\left( R \right):\,\,x - 2y + z - 4 = 0\). Một đường thẳng d thay đổi cắt ba mặt phẳng \(\left( P \right);\left( Q \right);\left( R \right)\) lần lượt tại A, B, C. Đặt \(T = \dfrac{{A{B^2}}}{4} + \dfrac{{144}}{{AC}}\). Tìm giá trị nhỏ nhất của \(T\).
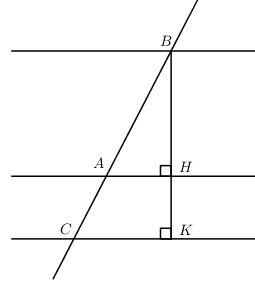
Dễ dàng thấy 3 mặt phẳng \(\left( P \right);\left( Q \right);\left( R \right)\) song song với nhau và (P) nằm giữa (Q) và (R), ta tính được \(d\left( {\left( P \right);\left( Q \right)} \right) = BH = 9;\,\,d\left( {\left( P \right);\left( R \right)} \right) = HK = 3\)
Ta có:
$\begin{array}{l}T = \dfrac{{A{B^2}}}{4} + \dfrac{{144}}{{AC}} = \dfrac{{A{B^2}}}{4} + \dfrac{{72}}{{AC}} + \dfrac{{72}}{{AC}}\\\mathop \ge \limits^{Cauchy} 3\sqrt[3]{{\dfrac{{A{B^2}}}{4}.\dfrac{{72}}{{AC}}.\dfrac{{72}}{{AC}}}} = 3\sqrt[3]{{1296.{{\left( {\dfrac{{AB}}{{AC}}} \right)}^2}}}\end{array}$
Theo định lí Ta-let ta có :
$\dfrac{{AB}}{{AC}} = \dfrac{{BH}}{{HK}} = 3 \Rightarrow T\mathop \ge \limits^{Cauchy} 3\sqrt[3]{{{{1296.3}^2}}} = 54\sqrt[3]{2}$
Vậy \(\min T = 54\sqrt[3]{2}\).
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với $A(1;0;0),\,\,B(3;2;4),\,C(0;5;4)$. Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $\left| {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right|$ nhỏ nhất.
+ Ta tìm điểm \(I\left( {a;b;c} \right)\) thỏa mãn \(\overrightarrow {IA} + \overrightarrow {IB} + 2\overrightarrow {IC} = \overrightarrow 0 \) hay:
\(\left\{ \begin{array}{l}1 - a + 3 - a - 2a = 0\\ - b + 2 - b + 2\left( {5 - b} \right) = 0\\ - c + 4 - c + 2\left( {4 - c} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 3\\c = 3\end{array} \right. \Rightarrow I\left( {1;3;3} \right)\)
+ Khi đó:
$\left| {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right| = \left| {4\overrightarrow {MI} } \right| \ge 4IH$ với \(H\) là hình chiếu của \(I\) trên \(\left( {Oxy} \right)\) và \(H\left( {1;3;0} \right)\)
Do đó \(\min \left| {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right| = 4IH = 12\) khi \(H \equiv M\) hay \(M\left( {1;3;0} \right)\)
Trong không gian với hệ tọa độ $Oxyz,$ cho ba điểm $A\left( {3;0;0} \right),\,\,B\left( {1;2;1} \right)$ và $C\left( {2; - \,1;2} \right).$ Biết mặt phẳng qua $B,\,\,C$ và tâm mặt cầu nội tiếp tứ diện $OABC$ có một vectơ pháp tuyến là $\left( {10;a;b} \right).$ Tổng $a + b$ là
Phương trình mặt phẳng $\left( {OBC} \right)$ là $x - z = 0.$
Phương trình mặt phẳng $\left( {ABC} \right)$ là $5x + 3y + 4z - 15 = 0.$
Gọi $I\left( {x;y;z} \right)$ là tâm mặt cầu nội tiếp tứ diện $OABC$$ \Rightarrow \,\,d\left( {I;\left( {OBC} \right)} \right) = d\left( {I;\left( {ABC} \right)} \right)$
$\dfrac{{\left| {x - z} \right|}}{{\sqrt 2 }} = \dfrac{{\left| {5x + 3y + 4z - 15} \right|}}{{5\sqrt 2 }} \Leftrightarrow \left| {5x - 5z} \right| = \left| {5x + 3y + 4z - 15} \right|$$ \Leftrightarrow \left[ \begin{array}{l}y + 3z - 5 = 0\\10x + 3y - z - 15 = 0\end{array} \right.$
Mà mặt phẳng cần tìm có dạng $10x + ay + bz + d = 0$$ \Rightarrow \,\,I \in \left( \alpha \right):10x + 3y - z - 15 = 0.$
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $A\left( {1;1;1} \right)$ và đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{y}{{ - \,2}} = \dfrac{{z - 1}}{9}.$ Biết đường thẳng $\Delta $ qua $A,$ cắt $d$ và khoảng cách từ gốc tọa độ đến $\Delta $ nhỏ nhất, $\Delta $ có một vectơ chỉ phương là $\left( {1;a;b} \right).$ Tổng $a + b$ là
Đường thẳng $d$ đi qua $B\left( {1;0;1} \right),$ có vectơ chỉ phương $\vec u = \left( {1; - \,2;9} \right)$$ \Rightarrow \,\,\left[ {\overrightarrow {AB} ;\vec u} \right] = \left( {9;0; - \,1} \right).$
Phương trình mặt phẳng $\left( \alpha \right)$ chứa $d$ và đi qua $A$ là $\left( \alpha \right):9x - z - 8 = 0.$
Gọi $I$ là hình chiếu của $O$ trên $\Delta ,$ $H$ là hình chiếu của $O$ trên $\left( \alpha \right).$
Ta có $d\left( {O;\left( \Delta \right)} \right) = OI \le OH \Rightarrow \,\,{d_{\min }} = OH$$ \Leftrightarrow $$H$ là hình chiếu của $O$ trên $\left( \alpha \right).$
Phương trình đường thẳng $OH$ là $\left\{ \begin{array}{l}x = 9t\\y = 0\\z = - \,t\end{array} \right.$$ \Rightarrow \,\,H\left( {9t;0; - \,t} \right) \in \left( \alpha \right)$$ \Rightarrow t = \dfrac{4}{{41}}.$
Vậy $H\left( {\dfrac{{36}}{{41}};0; - \,\dfrac{4}{{41}}} \right) \Rightarrow \overrightarrow {HA} = \left( {\dfrac{5}{{41}};1;\dfrac{{45}}{{41}}} \right) = \dfrac{5}{{41}}\left( {1;\dfrac{{41}}{5};9} \right) \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{41}}{5}\\b = 9\end{array} \right..$
\( \Rightarrow a + b = \dfrac{{41}}{5} + 9 = \dfrac{{86}}{5}.\)
Trong không gian Oxyz, cho hai đường thẳng ${d_1}:\dfrac{{x - 1}}{2} = \dfrac{y}{{ - 1}} = \dfrac{{z + 2}}{1}$ và ${d_2}:\dfrac{{x + 1}}{1} = \dfrac{{y - 1}}{7} = \dfrac{{z - 3}}{{ - 1}}$. Đường vuông góc chung của ${d_1}$ và ${d_2}$ lần lượt cắt ${d_1},\,\,{d_2}$ tại A và B. Diện tích tam giác OAB bằng
${d_1}:\dfrac{{x - 1}}{2} = \dfrac{y}{{ - 1}} = \dfrac{{z + 2}}{1}$ có phương trình tham số : $\left\{ \begin{array}{l}x = 1 + 2{t_1}\\y = - {t_1}\\z = - 2 + {t_1}\end{array} \right.$, có 1 VTCP $\overrightarrow {{u_1}} \left( {2; - 1;1} \right)$.
${d_2}:\dfrac{{x + 1}}{1} = \dfrac{{y - 1}}{7} = \dfrac{{z - 3}}{{ - 1}}$ có phương trình tham số : $\left\{ \begin{array}{l}x = - 1 + {t_2}\\y = 1 + 7{t_2}\\z = 3 - {t_2}\end{array} \right.$, có 1 VTCP $\overrightarrow {{u_1}} \left( {1;7; - 1} \right)$.
$A \in {d_1},\,\,B \in {d_2}$
Gọi $A(1 + 2{t_1}; - {t_1}; - 2 + {t_1}),\,\,B( - 1 + {t_2};1 + 7{t_2};3 - {t_2}) \Rightarrow \overrightarrow {AB} = \left( {{t_2} - 2{t_1} - 2;7{t_2} + {t_1} + 1;\, - {t_2} - {t_1} + 5} \right)$
AB là đường vuông góc chung của ${d_1},\,\,{d_2}$ $ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{u_1}} = 0\\\overrightarrow {AB} .\overrightarrow {{u_2}} = 0\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}2({t_2} - 2{t_1} - 2) - 1(7{t_2} + {t_1} + 1) + 1( - {t_2} - {t_1} + 5) = 0\\1({t_2} - 2{t_1} - 2) + 7(7{t_2} + {t_1} + 1) - 1( - {t_2} - {t_1} + 5) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6{t_2} - 6{t_1} = 0\\51{t_2} + 6{t_1} = 0\end{array} \right. \Leftrightarrow {t_1} = {t_2} = 0$
$ \Rightarrow A(1;0; - 2),\,\,B( - 1;1;3) \Rightarrow \overrightarrow {OA} = (1;0; - 2),\,\,\overrightarrow {OB} = ( - 1;1;3)$
Diện tích tam giác OAB: ${S_{OAB}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right]} \right| = \dfrac{1}{2}\left| {\left( {2; - 1;1} \right)} \right| = \dfrac{{\sqrt 6 }}{2}$
Trong không gian ${\rm{Ox}}yz$, cho đường thẳng $d:\,\,\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z - 1}}{2}$ và hai điểm $A(3;2;1)$, $B(2;0;4)$. Gọi $\Delta $ là đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến $\Delta $ là nhỏ nhất. Gọi $\overrightarrow u = (2;b;c)$ là một VTCP của $\Delta $. Khi đó, $\left| {\overrightarrow u } \right|$ bằng
$\overrightarrow {AB} = \left( { - 1; - 2;3} \right)$
$d:\,\,\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z - 1}}{2}$ có 1 VTCP $\overrightarrow v \left( {1; - 2;2} \right)$ là một VTCP của $\Delta $
$\Delta $ là đường thẳng qua A, vuông góc với d $ \Rightarrow \Delta \subset \left( \alpha \right)$: mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng $\left( \alpha \right):1(x - 3) - 2(y - 2) + 2(z - 1) = 0 \Leftrightarrow x - 2y + 2z - 1 = 0$
Khi đó, $d{\left( {B;\Delta } \right)_{\min }} = d\left( {B;\left( \alpha \right)} \right)$ khi và chỉ khi $\Delta $ đi qua hình chiếu $H$ của B lên $\left( \alpha \right)$.
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua $B(2;0;4)$ và có VTCP là VTPT của $\left( \alpha \right)$ có phương trình: $\left\{ \begin{array}{l}x = 2 + t\\y = - 2t\\z = 4 + 2t\end{array} \right.$ $H \in BH \Rightarrow H\left( {2 + t; - 2t;4 + 2t} \right)$
$H \in \left( \alpha \right) \Rightarrow (2 + t) - 2( - 2t) + 2(4 + 2t) - 1 = 0 \Leftrightarrow 9t + 9 = 0 \Leftrightarrow t = - 1 \Rightarrow H\left( {1;2;2} \right)$
$\Delta $ đi qua $A(3;2;1)$, $H\left( {1;2;2} \right)$ có VTCP $\overrightarrow {HA} = \left( {2;0; - 1} \right) = \overrightarrow u \left( {2;b;c} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt 5 $
