Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ Oxyz cho ba mặt phẳng \(\left( P \right):\,\,x - 2y + z - 1 = 0\), \(\left( Q \right):\,\,x - 2y + z + 8 = 0\) và \(\left( R \right):\,\,x - 2y + z - 4 = 0\). Một đường thẳng d thay đổi cắt ba mặt phẳng \(\left( P \right);\left( Q \right);\left( R \right)\) lần lượt tại A, B, C. Đặt \(T = \dfrac{{A{B^2}}}{4} + \dfrac{{144}}{{AC}}\). Tìm giá trị nhỏ nhất của \(T\).
Trả lời bởi giáo viên
Đáp án đúng: b
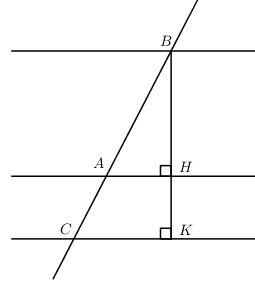
Dễ dàng thấy 3 mặt phẳng \(\left( P \right);\left( Q \right);\left( R \right)\) song song với nhau và (P) nằm giữa (Q) và (R), ta tính được \(d\left( {\left( P \right);\left( Q \right)} \right) = BH = 9;\,\,d\left( {\left( P \right);\left( R \right)} \right) = HK = 3\)
Ta có:
$\begin{array}{l}T = \dfrac{{A{B^2}}}{4} + \dfrac{{144}}{{AC}} = \dfrac{{A{B^2}}}{4} + \dfrac{{72}}{{AC}} + \dfrac{{72}}{{AC}}\\\mathop \ge \limits^{Cauchy} 3\sqrt[3]{{\dfrac{{A{B^2}}}{4}.\dfrac{{72}}{{AC}}.\dfrac{{72}}{{AC}}}} = 3\sqrt[3]{{1296.{{\left( {\dfrac{{AB}}{{AC}}} \right)}^2}}}\end{array}$
Theo định lí Ta-let ta có :
$\dfrac{{AB}}{{AC}} = \dfrac{{BH}}{{HK}} = 3 \Rightarrow T\mathop \ge \limits^{Cauchy} 3\sqrt[3]{{{{1296.3}^2}}} = 54\sqrt[3]{2}$
Vậy \(\min T = 54\sqrt[3]{2}\).
Hướng dẫn giải:
3 mặt phẳng \(\left( P \right);\left( Q \right);\left( R \right)\) song song với nhau và (P) nằm giữa (Q) và (R), tính khoảng cách giữa các mặt phẳn song song.
Phân tích \(T = \dfrac{{A{B^2}}}{4} + \dfrac{{144}}{{AC}} = \dfrac{{A{B^2}}}{4} + \dfrac{{72}}{{AC}} + \dfrac{{72}}{{AC}}\), sử dụng BĐT Cauchy cho ba số không âm \(a + b + c \ge 3\sqrt[3]{{abc}}\) và định lí Ta-let.
