Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {3;0;0} \right)\), \(B\left( {0; - 6;0} \right)\), \(C\left( {0;0;6} \right)\) và mặt phẳng \(\left( \alpha \right):x + y + z - 4 = 0\). Tọa độ hình chiếu vuông góc của trọng tâm tam giác \(ABC\) lên mặt phẳng \(\left( \alpha \right)\) là:
Trọng tâm của tam giác \(ABC\) là \(G\left( {1; - 2;2} \right)\).
Gọi \(d\) là đường thẳng qua \(G\) và vuông góc với mặt phẳng \(\left( \alpha \right)\). Khi đó \(H = d \cap \left( \alpha \right)\) chính là hình chiếu vuông góc của \(G\) lên mặt phẳng \(\left( \alpha \right)\).
Phương trình tham số của \(d:\left\{ \begin{array}{l}x = 1 + t\\y = - 2 + t\\z = 2 + t\end{array} \right.\) , thay vào phương trình mặt phẳng \(\left( \alpha \right)\) ta có:
\(\left( {1 + t} \right) + \left( { - 2 + t} \right) + \left( {2 + t} \right) - 4 = 0 \Leftrightarrow t = 1 \Rightarrow H\left( {2; - 1;3} \right)\).
Trong không gian với hệ trục tọa độ $O x y z$, cho hai đường thẳng \({\ell _1}:x - 1 = \dfrac{{y + 2}}{2} = - z\) và \({\ell _2}:\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 1}}{2}\). Gọi \((Q)\) là mặt phẳng chứa \({\ell _1}\) và tạo với \({\ell _2}\) một góc lớn nhất là \(\alpha \). Khi đó \(\cos \alpha \) bằng
Bước 1: Giả sử phương trình của \((Q)\) có dạng \(A(x - 1) + B(y + 2) + Cz = 0\). Gọi \(\theta \) là góc giữa \((Q)\) và \({\ell _2}\). Biểu diễn \(\sin \theta \) theo A, B.
Đường thẳng \({\ell _1}\) có một vectơ chỉ phương là \({\vec u_1} = (1;2; - 1)\) và đi qua điểm \({M_1} = (1; - 2;0).\) Vì \((Q)\) chứa \({\ell _1}\) nên đi qua \({M_1}\) và vectơ pháp tuyến của nó vuông góc với \({\vec u_1}.\) Do đó, ta có thể giả sử phương trình của \((Q)\) có dạng
\(A(x - 1) + B(y + 2) + Cz = 0\) với \(1 \cdot A + 2 \cdot B + ( - 1) \cdot C = 0\) và \({A^2} + {B^2} + {C^2} > 0\)
Gọi \(\theta \) là góc giữa \((Q)\) và \({\ell _2}\).
Do vectơ pháp tuyến của \((Q)\) là \(\vec n = (A;B;C) = \) \((A;B;A + 2B)\) (vì \(A + 2B = C\)) và vectơ chỉ phương của \({\ell _2}\) là \({\vec u_2} = (2; - 1;2)\) nên ta có:
\(\sin \theta = \dfrac{{|4A + 3B|}}{{3\sqrt {2{A^2} + 4AB + 5{B^2}} }}\)\( = \dfrac{1}{3}\sqrt {\dfrac{{{{(4A + 3B)}^2}}}{{2{A^2} + 4AB + 5{B^2}}}} \)
Bước 2: Ta xét hai trường hợp của B để tìm \(\sin \theta \) rồi so sánh.
Ta xét hai trường hợp.
+) Trường hợp \(B = 0\), thì \(\sin \theta = \dfrac{{2\sqrt 2 }}{3}\).
+) Trường hợp \(B \ne 0\), ta đặt \(r = \dfrac{A}{B}\) thì được \(\sin \theta = \dfrac{1}{3}\sqrt {\dfrac{{{{(4r + 3)}^2}}}{{2{r^2} + 4r + 5}}} \).
Từ đó, ta xét hàm số \(f(r) = \dfrac{{{{(4r + 3)}^2}}}{{2{r^2} + 4r + 5}}\) trên \(\mathbb{R}\).
\({f^\prime }(r)\)\( = \dfrac{{8(4r + 3)\left( {2{r^2} + 4r + 5} \right) - {{(4r + 3)}^2}(4r + 4)}}{{{{\left( {2{r^2} + 4r + 5} \right)}^2}}}\)\( = \dfrac{{4(4r + 3)(r + 7)}}{{{{\left( {2{r^2} + 4r + 5} \right)}^2}}}\)
Mặt khác \(\mathop {\lim }\limits_{r \to \pm \infty } f(r) = 8\) và \(f\left( { - \dfrac{3}{4}} \right) = 0,f( - 7) = \dfrac{{25}}{3}\) nên ta lập được bảng biến thiên.
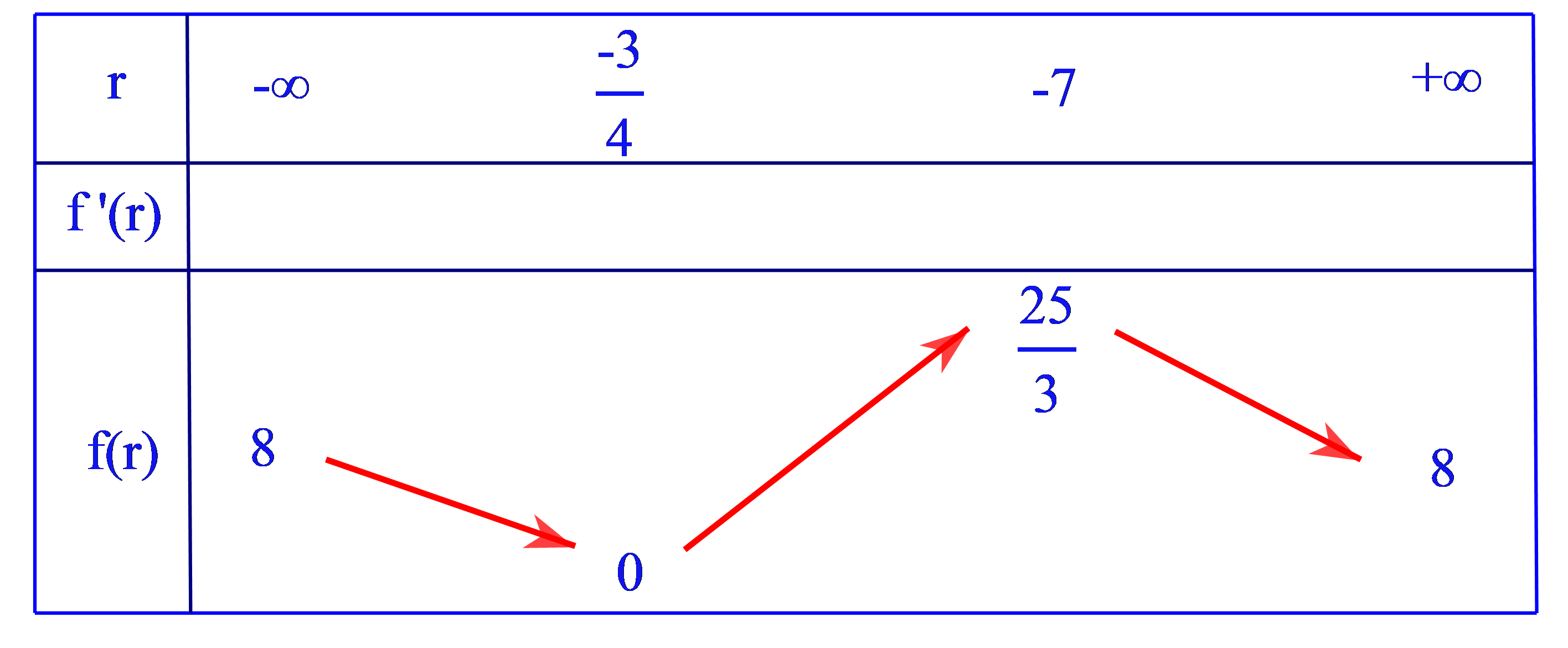
Từ đó thu được giá trị lớn nhất là \(\dfrac{{25}}{3}\). Khi đó, \(\sin \theta = \dfrac{{5\sqrt 3 }}{9}\).
So sánh hai trường hợp trên, ta thu được \(\sin \alpha = \dfrac{{5\sqrt 3 }}{9}\). Từ đó \(\cos \alpha = \dfrac{{\sqrt 6 }}{9}\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\dfrac{x}{{ - 1}} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right)\) có phương trình \(2x - y - 2z + 4 = 0\). Mặt phẳng chứa đường thẳng \(d\) và tạo với mặt phẳng \(\left( P \right)\) góc với số đo nhỏ nhất có phương trình là:
Giả sử \(\left( \alpha \right)\) cần tìm có 1 VTPT là \(\overrightarrow n = \left( {a;b;c} \right),\,\,\left( {{a^2} + {b^2} + {c^2} > 0} \right)\).
Do \(d \subset \left( \alpha \right)\) nên \(\overrightarrow n .\overrightarrow {{u_d}} = 0 \Leftrightarrow - a + 2b + c = 0 \Leftrightarrow a = 2b + c\)\( \Rightarrow \overrightarrow n = \left( {2b + c;b;c} \right)\)
Góc giữa hai mặt phẳng \(\left( \alpha \right),\left( P \right)\) được tính:
\(\cos \varphi = \dfrac{{\left| {\left( {2b + c} \right).2 - b - 2c} \right|}}{{3.\sqrt {{{\left( {2b + c} \right)}^2} + {b^2} + {c^2}} }} = \dfrac{{\left| b \right|}}{{\sqrt {5{b^2} + 4bc + 2{c^2}} }} = \sqrt {\dfrac{{{b^2}}}{{5{b^2} + 4bc + 2{c^2}}}} \)
+) \(b = 0 \Rightarrow \)\(\cos \varphi = 0 \Rightarrow \varphi = {90^0}\)
+) \(b \ne 0 \Rightarrow \)\(\cos \varphi = \sqrt {\dfrac{1}{{5 + 4.\dfrac{c}{b} + 2{{\left( {\dfrac{c}{b}} \right)}^2}}}} = \sqrt {\dfrac{1}{{2{{\left( {\dfrac{c}{b} + 1} \right)}^2} + 3}}} \Rightarrow 0 < \cos \varphi \le \dfrac{1}{{\sqrt 3 }}\)
\({\varphi _{\min }} \Leftrightarrow \dfrac{c}{b} = - 1\). Chọn \(b = 1,\,\,c = - 1\), khi đó \(a = 2.1 - 1 = 1 \Rightarrow \)\(\overrightarrow n = \left( {1;1; - 1} \right)\).
Do \(d \subset \left( \alpha \right) \Rightarrow A\left( {0; - 1;2} \right) \in \left( \alpha \right)\)
Phương trình mặt phẳng \(\left( \alpha \right)\) là: \(1\left( {x - 0} \right) + 1\left( {y + 1} \right) - 1\left( {z - 2} \right) = 0 \Leftrightarrow x + y - z + 3 = 0\).
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + 3y - z - 7 = 0\) và điểm \(A\left( {3;5;0} \right)\). Gọi \(A'\) là điểm đối xứng của \(A\) qua mặt phẳng \(\left( P \right)\). Điểm \(A'\) có tọa độ là:
Mặt phẳng \(\left( P \right)\) có VTPT \(\overrightarrow {{n_P}} = \left( {2;3; - 1} \right)\).
Gọi \(d\) là đường thẳng qua \(A\left( {3;5;0} \right)\) và vuông góc với \(\left( P \right)\) nên có VTCP \(\overrightarrow {{u_d}} = \overrightarrow {{n_P}} = \left( {2;3; - 1} \right)\).
Do đó \(d:\dfrac{{x - 3}}{2} = \dfrac{{y - 5}}{3} = \dfrac{z}{{ - 1}}\).
Tọa độ hình chiếu \(H\) vuông góc của \(A\) trên \(\left( P \right)\) là nghiệm của hệ \(\left\{ \begin{array}{l}\dfrac{{x - 3}}{2} = \dfrac{{y + 5}}{3} = \dfrac{z}{{ - 1}}\\2x + 3y - z - 7 = 0\end{array} \right. \Rightarrow H\left( {1;2;1} \right)\).
Khi đó \(H\) là trung điểm của \(AA'\) nên \(A'\left( { - 1; - 1;2} \right)\).
Trong không gian với hệ tọa độ Oxyz cho điểm $A(1;2; - 3)$và đường thẳng $d:\dfrac{{x - 1}}{{ - 1}} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{z}{3}$. Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng (d) là:
Ta có:
$\begin{array}{l}\left\{ \begin{array}{l}(P) \bot (d) \Rightarrow \overrightarrow {{n_P}} = \overrightarrow {{u_d}} = ( - 1; - 2;3)\\A(1;2; - 3) \in (P)\end{array} \right.\\ \Rightarrow (P): - 1(x - 1) - 2(y - 2) + 3(z + 3) = 0\\ \Leftrightarrow - x - 2y + 3z + 14 = 0\end{array}$
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ${\Delta _1}:\dfrac{{x - 2}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{{ - {\mkern 1mu} 3}}$ và ${\Delta _2}:\left\{ \begin{array}{l}x = t\\{\rm{ \;}}y = 2 - t\\{\rm{ \;}}z = 1 + 2t\end{array} \right.$. Phương trình mặt phẳng $\left( {\alpha {\rm{\;}}} \right)$ song song với hai đường thẳng ${\Delta _1},{\mkern 1mu} {\mkern 1mu} {\Delta _2}$ và cách điểm \(I\left( {1; - 1;3} \right)\) một khoảng bằng $\dfrac{{\sqrt {35} }}{5}$ là
Vì $\left\{ \begin{array}{l}{{\vec n}_\alpha } \bot {{\vec u}_1}\\{\rm{ \;}}{{\vec n}_\alpha } \bot {{\vec u}_2}\end{array} \right.$ suy ra ${\vec n_\alpha } = \left[ {{{\vec u}_1};{{\vec u}_2}} \right] = $$\left( {1; - {\mkern 1mu} 5; - {\mkern 1mu} 3} \right)$ nên $\left( {\alpha {\rm{\;}}} \right):x - 5y - 3z + m = 0.$
$d\left( {{\mathop{\rm I}\nolimits} ,\left( \alpha \right)} \right) = \dfrac{{\sqrt {35} }}{5} \Leftrightarrow \dfrac{{\left| {m - 3} \right|}}{{\sqrt {35} }} = \dfrac{{\sqrt {35} }}{5} \Rightarrow \left| {m - 3} \right| = 7 \Leftrightarrow \left[ \begin{array}{l}m = 10\\m = - 4\end{array} \right..$
Vậy ta thu được hai phương trình mặt phẳng là $(P_1):\,x - 5y - 3z + 10 = 0$ và $(P_2):\,x - 5y - 3z - 4 = 0.$
Nhận thấy đường thẳng $\Delta_1 $ nằm trong mặt phẳng \((P_2)\) nên chỉ có một mặt phẳng $(P_1):\,x - 5y - 3z + 10 = 0$ thỏa mãn yêu cầu đề bài.
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = - \dfrac{9}{5} - t\\y = 5t\\z = \dfrac{7}{5} + 3t\end{array} \right.\) và mặt phẳng \(\left( P \right):3x - 2y + 3z - 1 = 0\).
Gọi \(d'\) là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của \(d'\)?
Đường thẳng \(d\) có VTCP \(\overrightarrow {{u_d}} = \left( { - 1;5;3} \right)\).
Mặt phẳng \(\left( P \right)\) có VTPT \(\overrightarrow {{n_P}} = \left( {3; - 2;3} \right)\).
Gọi mặt phẳng \(\left( Q \right)\) chứa \(d\) và vuông góc với \(\left( P \right)\).
Suy ra VTPT của \(\left( Q \right)\) là \(\overrightarrow {{n_Q}} = \left[ {\overrightarrow {{u_d}} ,\overrightarrow {{n_P}} } \right] = \left( {21;12; - 13} \right)\).
Vì \(d'\) là hình chiếu của \(d\) lên mặt phẳng \(\left( P \right)\) nên \(d' = \left( Q \right) \cap \left( P \right)\).
Do đó \(d'\) có VTCP là \(\overrightarrow {{u_{d'}}} = \left[ {\overrightarrow {{n_{\left( P \right)}}} ,\overrightarrow {{n_{\left( Q \right)}}} } \right] = \left( {10; - 102; - 78} \right) = 2\left( {5; - 51; - 39} \right) = - 2\left( { - 5;51;39} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t{\rm{ }}}\\{y = 8 + 4t}\\{z = 3 + 2t}\end{array}} \right.\) và mặt phẳng $\left( P \right):x + y + z - 7 = 0.$ Phương trình đường thẳng \(\Delta '\) là hình chiếu vuông góc của \(\Delta \) trên \(\left( P \right)\) là:
Gọi \(\left( Q \right)\) là mặt phẳng chứa \(\Delta \) và vuông góc với \(\left( P \right)\), suy ra $\left( Q \right):2x + y - 3z + 1 = 0.$
Khi đó \(\Delta '\) cần tìm là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) nên thỏa mãn hệ $\left\{ \begin{array}{l}x + y + z - 7 = 0\\2x + y - 3z + 1 = 0\end{array} \right..$
Đặt \(z = t,\) ta có phương trình tham số của \(\Delta '\) là \(\left\{ {\begin{array}{*{20}{c}}{x = - 8 + 4t}\\{y = 15 - 5t}\\{z = t{\rm{ }}}\end{array}} \right..\)
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng $d:\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = - 1\end{array} \right.$, điểm $M\left( {1;2;1} \right)$ và mặt phẳng $\left( P \right):2x + y - 2z - 1 = 0$. Đường thẳng \(\Delta \) đi qua \(M\), song song với \(\left( P \right)\) và vuông góc với \(d\) có phương trình:
Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\overrightarrow {{n_P}} = \left( {2;1; - 2} \right)\).
Đường thẳng \(d\) có vectơ chỉ phương \(\overrightarrow {{u_d}} = \left( {1;2;0} \right)\).
Đường thẳng \(\Delta \) song song với \(\left( P \right)\) và vuông góc với \(d\) nên có VTCP
$\overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{n_P}} ,\overrightarrow {{u_d}} } \right] = \left( {4; - 2;3} \right)$.
Vậy phương trình đường thẳng \(\Delta :\dfrac{{x - 1}}{4} = \dfrac{{y - 2}}{{ - 2}} = \dfrac{{z - 1}}{3}\).
Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng $\left( \alpha \right):3x - 2y - z + 5 = 0$ và đường thẳng $\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y - 7}}{1} = \dfrac{{z - 3}}{4}$. Gọi $\left( \beta \right)$ là mặt phẳng chứa $\Delta $ và song song với mặt phẳng $\left( \alpha \right)$. Tính khoảng cách giữa $\left( \alpha \right)$ và $\left( \beta \right)$.
Đường thẳng \(\Delta \) đi qua $M\left( {1;7;3} \right)$.
Vì $\left( \beta \right)$ là mặt phẳng chứa $\Delta $ và song song với mặt phẳng $\left( \alpha \right)$ nên $d\left( {\left( \alpha \right),\left( \beta \right)} \right) = d\left( {M,\left( \alpha \right)} \right)$ $ = \dfrac{{\left| {3.1 - 2.7 - 3 + 5} \right|}}{{\sqrt {3{}^2 + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{9}{{\sqrt {14} }}$.
Trong không gian với hệ tọa độ Oxyz cho điểm $A(1;2;1)$và đường thẳng $(d):\dfrac{x}{3} = \dfrac{{y - 1}}{4} = z + 3$. Viết phương trình mặt phẳng (P) đi qua A và chứa đường thẳng d
Chọn $B(0;1; - 3) \in d$, suy ra \(B \in (P)\)
Ta có:$\left\{ \begin{array}{l}\overrightarrow {{u_d}} = \left( {3;4;1} \right)\\\overrightarrow {AB} = \left( { - 1; - 1; - 4} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {{u_d}} ;\overrightarrow {AB} } \right] = ( - 15;11;1)$
Vì (P) chứa đường thẳng d và đi qua A, B $ \Rightarrow \overrightarrow n = \left[ {\overrightarrow {{u_d}} ,\overrightarrow {AB} } \right]$ $ = ( - 15;11;1)$
Ta có:
\((P):\left\{ \begin{array}{l}\overrightarrow {{n_P}} = ( - 15;11;1)\\A(1;2;1) \in (P)\end{array} \right. \) \(\Rightarrow (P): - 15(x - 1) + 11(y - 2) + (z - 1) = 0 \) \(\Leftrightarrow - 15x + 11y + z - 8 = 0\)
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD có các đỉnh $A(1;2;1),B( - 2;1;3),C(2; - 1;1),D(0;3;1)$. Phương trình mặt phẳng (P) đi qua hai điểm A,B sao cho C,D khác phía so với (P) và khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P) là:
Gọi I là trung điểm của CD, suy ra $I(1;1;1)$
Vì C, D khác phía so với (P) và khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P) nên $I \in (P)$.
Do đó, mặt phẳng (P) đi qua 3 điểm A,B,I.
Ta có
\(\overrightarrow {AI} = (0; - 1;0);\overrightarrow {BI} = (3;0; - 2) \Rightarrow \left[ {\overrightarrow {AI} ;\overrightarrow {BI} } \right] = (2;0;3)\)
$(P):\left\{ \begin{array}{l}\overrightarrow {{n_P}} = \left[ {\overrightarrow {AI} ,\overrightarrow {BI} } \right]{\rm{ = }}\left( {{\rm{2;0;3}}} \right)\\A(1;2;1)\end{array} \right. \Rightarrow (P):2(x - 1) + 3(z - 1) = 0 \Leftrightarrow 2x + 3z - 5 = 0$
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y - 3}}{3} = \dfrac{z}{2}\), mặt phẳng \(\left( \alpha \right):x + y - z + 3 = 0\) và điểm \(A\left( {1;2 - 1} \right)\). Đường thẳng \(\Delta \) đi qua \(A\) cắt \(d\) và song song với mặt phẳng \(\left( \alpha \right)\) có phương trình là:
Mặt phẳng \(\left( \alpha \right)\) có VTPT \(\overrightarrow n = \left( {1;1; - 1} \right)\).
Gọi \(B = \Delta \cap d\), suy ra \(B \in d \Rightarrow B\left( {3 + t;3 + 3t;2t} \right)\).
Suy ra đường thẳng \(\Delta \) có VTCP \(\overrightarrow {AB} = \left( {2 + t;1 + 3t;1 + 2t} \right)\).
Vì \(\Delta \parallel \left( \alpha \right)\) nên \(\overrightarrow {AB} .\overrightarrow n = 0 \Leftrightarrow 2 + t + 1 + 3t - 2t - 1 = 0 \Leftrightarrow t = - 1\).
Do đó phương trình \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{{ - 2}} = \dfrac{{z + 1}}{{ - 1}}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {3;3;1} \right)\), \(B\left( {0;2;1} \right)\) và mặt phẳng \(\left( P \right):x + y + z - 7 = 0\). Đường thẳng \(d\) nằm trong \(\left( P \right)\) sao cho mọi điểm của \(d\) cách đều hai điểm \(A,{\rm{ }}B\) có phương trình là:
Phương trình mặt phẳng trung trực của \(AB\) là \(\left( \alpha \right):3x + y - 7 = 0\).
Đường thẳng cần tìm \(d\) cách đều hai điểm \(A,{\rm{ }}B\) nên sẽ thuộc mặt phẳng \(\left( \alpha \right)\).
Lại có \(d \subset \left( P \right)\), suy ra \(d = \left( P \right) \cap \left( \alpha \right)\) hay \(d:\left\{ \begin{array}{l}x + y + z - 7 = 0\\3x + y - 7 = 0\end{array} \right.\)
Chọn \(z = t\), ta được \(\left\{ \begin{array}{l}x = 2t\\y = 7 - 3t\\z = t\end{array} \right.\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,\,3x - y + z - 7 = 0\). Phương trình đường thẳng \(\Delta \) đi qua điểm \(A\left( {2; - 3;1} \right)\) và vuông góc với mặt phẳng \(\left( P \right)\) là:
Mặt phẳng \(\left( P \right):\,\,3x - y + z - 7 = 0\) có 1 VTPT \(\overrightarrow {{n_P}} = \left( {3; - 1;1} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng \(\left( P \right)\) nên có 1 VTCP là \(\overrightarrow {{u_\Delta }} = \overrightarrow {{n_P}} = \left( {3; - 1;1} \right)\).
Vậy phương trình tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l}x = 2 + 3t\\y = - 3 - t\\z = 1 + t\end{array} \right.\).
Trong không gian \(Oxyz\), cho đường thẳng \(d\) vuông góc với mặt phẳng \(\left( P \right):2x + 2y + z - 1 = 0\). Vecto nào sau đây là một vecto chỉ phương của \(d\)?
Mặt phẳng \(\left( P \right):2x + 2y + z - 1 = 0\) có vecto pháp tuyến là \(\overrightarrow n = \left( {2;2;1} \right)\).
Vì đường thẳng \(d \bot \left( P \right)\) nên đường thẳng \(d\) có 1 VTCP \(\overrightarrow {{u_d}} = \overrightarrow n = \left( {2;2;1} \right)\).
Cho đường thẳng \(\left( d \right)\) nằm trên mặt phẳng \(\left( P \right):x + y + z - 3 = 0\) và vuông góc với đường thẳng \(\left( {d'} \right):\,\,\,\dfrac{{x - 1}}{1} = \dfrac{y}{3} = \dfrac{z}{{ - 1}}\) . Tìm một vecto chỉ phương của đường thẳng \(\left( d \right)\).
Ta có:
\(\overrightarrow {{n_{\left( P \right)}}} = \left( {1;1;1} \right)\) là 1VTPT của (P).
\(\overrightarrow {{u_{d'}}} = \left( {1;3; - 1} \right)\) là một 1VTCP của (d’).
Ta có: \(\left\{ \begin{array}{l}d \bot d' \Rightarrow \overrightarrow {{u_d}} \bot \overrightarrow {{u_{d'}}} \\d \subset \left( P \right) \Rightarrow \overrightarrow {{u_d}} \bot \overrightarrow {{n_{\left( P \right)}}} \end{array} \right.\)\( \Rightarrow \)\(\overrightarrow {{u_d}} \) cùng phương với \(\left[ {\overrightarrow {{u_{d'}}} ,\overrightarrow {{n_{\left( P \right)}}} } \right]\).
Lại có: \(\left[ {\overrightarrow {{u_{d'}}} ,\overrightarrow {{n_{\left( P \right)}}} } \right] = \left( {\left| \begin{array}{l}1\,\,\,\,\,\,\,1\\3\,\,\, - 1\end{array} \right|;\left| \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,1\\ - 1\,\,\,\,\,\,1\end{array} \right|;\left| \begin{array}{l}1\,\,\,\,\,\,\,1\\1\,\,\,\,\,\,\,3\end{array} \right|} \right) = \left( { - 4;2;2} \right)\).
Do đó có thể chọn \(\overrightarrow {{u_d}} = \dfrac{1}{2}\left[ {\overrightarrow {{u_{d'}}} ,\overrightarrow {{n_{\left( P \right)}}} } \right] = \dfrac{1}{2}\left( { - 4;2;2} \right) = \left( { - 2;1;1} \right)\) làm 1 VTCP của (d).
Cho tam giác \(ABC\) có \(A\left( {3;0;0} \right),\)\(B\left( {0; - 6;0} \right),\)\(C\left( {0;0;6} \right)\). Tìm tọa độ điểm \(H\) là hình chiếu vuông góc của trọng tâm tam giác \(ABC\) trên mặt phẳng \(x + y + z - 4 = 0\).
Gọi \(G\) là trọng tâm tam giác \(ABC\) thì \(G\left( {1; - 2;2} \right)\).
Gọi \(\Delta \) là đường thẳng đi qua \(G\) và vuông góc với \(\left( \alpha \right):x + y + z - 4 = 0\).
Khi đó \(\overrightarrow {{u_\Delta }} = \overrightarrow {{n_{\left( \alpha \right)}}} = \left( {1;1;1} \right)\) nên \(\Delta \) có phương trình: \(\left\{ \begin{array}{l}x = 1 + t\\y = - 2 + t\\z = 2 + t\end{array} \right.,t \in \mathbb{R}\)
Vì \(H\) là hình chiếu của \(G\) lên \(\left( \alpha \right)\) nên \(H = \Delta \cap \left( \alpha \right)\).
Khi đó, tọa độ điểm \(H\) thỏa mãn : \(\left\{ \begin{array}{l}x = 1 + t\\y = - 2 + t\\z = 2 + t\\x + y + z - 4 = 0\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \left( {1 + t} \right) + \left( { - 2 + t} \right) + \left( {2 + t} \right) - 4 = 0\\ \Leftrightarrow - 3 + 3t = 0 \Leftrightarrow t = 1.\end{array}\)
Vậy \(H\left( {2; - 1;3} \right)\).
Trong không gian \(Oxyz\), cho đường thẳng d: \(\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{1} = \dfrac{z}{{ - 2}}\) và điểm \(A\left( {3;1; - 1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua \(A\) và chứa đường thẳng \(d\). Điểm nào dưới đây thuộc \(\left( \alpha \right)\)?
Ta có đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{1} = \dfrac{z}{{ - 2}}\) có 1 vecto chỉ phương là \(\overrightarrow {{u_d}} = \left( {2;1; - 2} \right)\) và đi qua \(B\left( { - 1;1;0} \right)\).
Ta có: \(A\left( {3;1; - 1} \right) \Rightarrow \overrightarrow {AB} = \left( { - 4;0;1} \right)\) \( \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {{u_d}} } \right] = \left( {1;6;4} \right)\).
Gọi \(\overrightarrow {{n_\alpha }} \) là 1 vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) ta có: \(\left\{ \begin{array}{l}d \subset \left( \alpha \right) \Rightarrow \overrightarrow {{n_\alpha }} \bot \overrightarrow {{u_d}} \\AB \subset \left( \alpha \right) \Rightarrow \overrightarrow {{n_\alpha }} \bot \overrightarrow {AB} \end{array} \right.\) \( \Rightarrow \overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {AB} ;\overrightarrow {{u_d}} } \right] = \left( {1;6;4} \right)\).
Mặt phẳng \(\left( \alpha \right)\) đi qua \(A\left( {3;1; - 1} \right)\) và có 1 VTPT \(\overrightarrow {{n_\alpha }} = \left( {1;6;4} \right)\) có phương trình là:
\(1.\left( {x - 3} \right) + 6.\left( {y - 1} \right) + 4.\left( {z + 1} \right) = 0\) \( \Leftrightarrow x + 6y + 4z - 5 = 0\).
Thay tọa độ điểm \(M\left( {1;0;1} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\) ta có: \(1 + 6.0 + 4.1 - 5 = 0 \Rightarrow M \in \left( \alpha \right)\).
Đề thi THPT QG - 2021 - mã 103
Trong không gian \(Oxyz\), cho điểm \(M\left( {1;2; - 1} \right)\) và mặt phẳng \(\left( P \right):\,\,2x + y - 3z + 1 = 0\). Đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) có phương trình là:
Gọi \(d\) là đường thẳng cần tìm ta có: \(d \bot \left( P \right) \Rightarrow \overrightarrow {{u_d}} = \overrightarrow {{n_P}} = \left( {2;1; - 3} \right)\).
\( \Rightarrow \) Phương trình \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{1} = \dfrac{{z + 1}}{{ - 3}}\).

