Tổng hợp câu hay và khó chương 4 phần 3

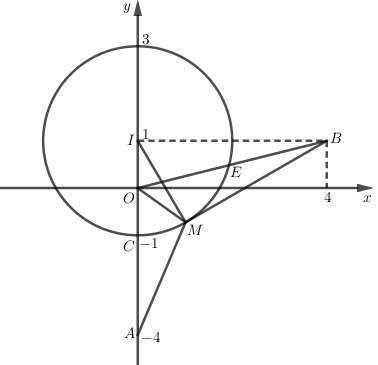
Trên mặt phẳng tọa độ Oxy, gọi \(A\left( 0;-3 \right)\) là điểm biểu diễn số phức \({{z}_{1}};\,\,B\left( 4;1 \right)\) là điểm biểu diễn số phức \({{z}_{2}};\,\,I\left( 0;1 \right)\) là điểm biểu diễn số phức i và M là điểm biểu diễn cho số phức z.

Theo đề bài ta có \(\left| z-i \right|=2\Rightarrow MI=2\Rightarrow \) M thuộc đường tròn tâm I bán kính R = 2.

\(T=\left| z-{{z}_{1}} \right|+2\left| z-{{z}_{2}} \right|=MA+2MB\).

Ta có IM = 2, IO = 1, IA = 4 \(\Rightarrow I{{M}^{2}}=IA.IO\Leftrightarrow \dfrac{IM}{IA}=\dfrac{IO}{IM}\).

Do đó tam giác IMO đồng dạng với tam giác IAM \(\Rightarrow \dfrac{IM}{IA}=\dfrac{OM}{AM}=\dfrac{1}{2}\Rightarrow MA=2MO\)

\(\Rightarrow T=MA+2MB=2MO+2MB=2\left( MO+MB \right)\ge 2OB\).

Dấu bằng xảy ra khi và chỉ khi M là giao điểm của OB và (I) \(\Leftrightarrow M\equiv E\).

\(O\left( 0;0 \right);\,\,B\left( 4;1 \right)\Rightarrow \) Phương trình OB là \(y=\dfrac{1}{4}x\,\,\left( d \right);\,\,E\in d\Rightarrow E\left( 4m;m \right)\,\,\,\left( m>0 \right)\).

Vì \(E\in \left( I \right)\Rightarrow IE=2\Rightarrow {{\left( 4m \right)}^{2}}+{{\left( m-1 \right)}^{2}}=4\Leftrightarrow 17{{m}^{2}}-2m-3=0\Leftrightarrow m=\dfrac{1+2\sqrt{13}}{17}\,\,\left( m>0 \right)\)

Ta có \(\left\{ \begin{align}  a=4m \\  b=m \\ \end{align} \right.\Rightarrow a-b=3m=\dfrac{3+6\sqrt{13}}{17}\).

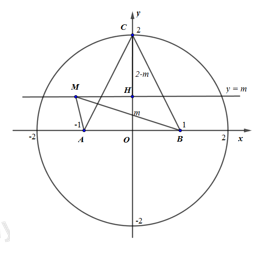
Giả sử \(z=x+yi,\,\,\left( x,y\in R \right)\Rightarrow M(x;y)\) là điểm biểu diễn của \(z\)trên mặt phẳng tọa độ Oxy.

\(P=2\left| z+1 \right|+2\left| z-1 \right|+\left| z-\overline{z}-4i \right|=2\left( \sqrt{{{(x+1)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\left| y-2 \right| \right)\)

Đặt \(A(-1;0),\,\,B(1;0),\,\,C(0;2)\) và \(H(0;y)\) là hình chiếu của M lên Oy. Khi đó, \(P=2\left( MA+MB+HC \right)\)

Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, ( M di chuyển trên hình tròn \({{x}^{2}}+{{y}^{2}}\le 4\))

+) Nếu \(M\in ({{C}_{1}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y<0\)thì ta luôn tìm được điểm \(M'\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\) đối xứng với \(M\)qua Ox. Khi đó

\(P=2\left( MA+MB+HC \right)=2\left( M'A+M'B+H'C \right)>2\left( MA+MB+HC \right)\)

+) Ta xét điểm \(M\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\)

Với M nằm trong nửa hình tròn \(({{C}_{2}})\), thay đổi trên đường thẳng \(y=m\) cố định \(\left( 0\le m\le 2 \right)\) thì độ dài đoạn HC không đổi, \(MA+MB\ge HA+HB=2HA\)

\(P=2\left( MA+MB+HC \right)\ge 2\left( 2HA+HC \right)\)

Ta có: \(2HA+HC=2\sqrt{{{m}^{2}}+1}+2-m=f(m),\,\,m\in \left[ 0;2 \right]\)

\(f'(m)=\dfrac{2}{\sqrt{{{m}^{2}}+1}}-1,\,\,\,f'(m)=0\Leftrightarrow m=\dfrac{1}{\sqrt{3}}\)

\(f{{(m)}_{\min }}=f\left( \dfrac{1}{\sqrt{3}} \right)=1+\dfrac{\sqrt{3}}{2}\)

 \(\Rightarrow {{P}_{\min }}=2\left( 1+\dfrac{\sqrt{3}}{2} \right)=2+\sqrt{3}\) khi \(M\left( 0;\dfrac{1}{\sqrt{3}} \right)\,\,hay\,\,z=\dfrac{i}{\sqrt{3}}\) .

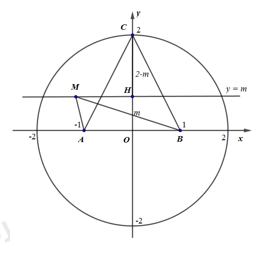
Giả sử \(z=x+yi,\,\,\left( x,y\in R \right)\Rightarrow M(x;y)\) là điểm biểu diễn của \(z\) trên mặt phẳng tọa độ Oxy.

\(P=2\left| z+1 \right|+2\left| z-1 \right|+\left| z-\overline{z}-4i \right|=2\left( \sqrt{{{(x+1)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\left| y-2 \right| \right)\)

Đặt \(A(-1;0),\,\,B(1;0),\,\,C(0;2)\) và \(H(0;y)\) là hình chiếu của M lên Oy. Khi đó, \(P=2\left( MA+MB+HC \right)\)

Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, (M di chuyển trên hình tròn \({{x}^{2}}+{{y}^{2}}\le 4\))

+) Nếu \(M\in ({{C}_{1}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y<0\)thì ta luôn tìm được điểm \(M'\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\) đối xứng với \(M\)qua Ox. Khi đó

\(P=2\left( MA+MB+HC \right)=2\left( M'A+M'B+H'C \right)>2\left( MA+MB+HC \right)\)

+) Ta xét điểm \(M\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\)

Với M nằm trong nửa hình tròn \(({{C}_{2}})\), thay đổi trên đường thẳng \(y=m\) cố định \(\left( 0\le m\le 2 \right)\) thì độ dài đoạn HC không đổi, \(MA+MB\ge HA+HB=2HA\)

\(P=2\left( MA+MB+HC \right)\ge 2\left( 2HA+HC \right)\)

Ta có: \(2HA+HC=2\sqrt{{{m}^{2}}+1}+2-m=f(m),\,\,m\in \left[ 0;2 \right]\)

\(f'(m)=\dfrac{2m}{\sqrt{{{m}^{2}}+1}}-1,\,\,\,f'(m)=0\Leftrightarrow m=\dfrac{1}{\sqrt{3}}\)

\(f{{(m)}_{\min }}=f\left( \dfrac{1}{\sqrt{3}} \right)=2+\sqrt 3\)

\(\Rightarrow {{P}_{\min }}=2\left( 2+\sqrt 3 \right)=4+2\sqrt{3}\) khi \(M\left( 0;\dfrac{1}{\sqrt{3}} \right)\,\,hay\,\,z=\dfrac{i}{\sqrt{3}}\).

Theo bài ra, ta có:

+) \(\left| z-1-i \right|=1\Rightarrow \)
Tập hợp biểu diễn số phức \(z\) là đường tròn \(\left( {{C}_{1}} \right)\) có tâm \({{I}_{1}}\left( 1;1 \right)\) và bán kính \({{R}_{1}}=1\).
+) \(\left| \bar{w}-2-3i \right|=2\Leftrightarrow \left| w-2+3i \right|=2\Rightarrow \)
Tập hợp biểu diễn số phức \(w\) là đường tròn \(\left( {{C}_{2}} \right)\) có tâm \({{I}_{2}}\left( 2;-\,3 \right)\) và bán kính \({{R}_{2}}=2.\)

Do \({{I}_{1}}{{I}_{2}}>{{R}_{1}}+{{R}_{2}}\) nên hai đường tròn không cắt nhau.

Khi đó \(\left| z-w \right|=MN\Rightarrow {{\left| z-w \right|}_{\min }}=M{{N}_{\min }}={{I}_{1}}{{I}_{2}}-\left( {{R}_{1}}+{{R}_{2}} \right)=\sqrt{17}-3\)

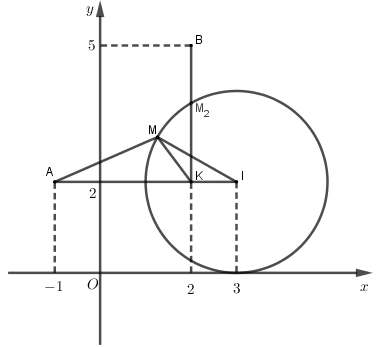
Cách 1: Đặt \(z-3-2i=w\) với \(w=x+yi\) \(\left( x,y\in \mathbb{R} \right)\).
Theo bài ra ta có \(\left| w \right|=2\Leftrightarrow {{x}^{2}}+{{y}^{2}}=4\).
Ta có \(P=\left| z+1-2i \right|+2\left| z-2-5i \right|=\left| w+4 \right|+2\left| w+1-3i \right|=\sqrt{{{\left( x+4 \right)}^{2}}+{{y}^{2}}}+2\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}\) \(\begin{align} & =\sqrt{20+8x}+2\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=2\sqrt{5+2x}+2\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \\ & =2\left( \sqrt{{{x}^{2}}+{{y}^{2}}+2x+1}+\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \right)=2\left( \sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}+\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}} \right) \\ & \ge 2\left( \left| y \right|+\left| y-3 \right| \right)\ge 2\left| y+3-y \right|=6. \\ \end{align}\)
Do đó
\(P = 6 \Leftrightarrow \left\{ \begin{array}{l}
x = - 1\\
y\left( {3 - y} \right) \ge 0\\
{x^2} + {y^2} = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = - 1\\
y = \sqrt 3
\end{array} \right.\)
Vậy GTNN của \(P\) là bằng \(6\) đạt được khi \(z=2+\left( 2+\sqrt{3} \right)i\). \(\Rightarrow a+b=2+2+\sqrt{3}=4+\sqrt{3}.\)
Cách 2: Giả thiết \(\left| z-3-2i \right|=2\)\(\Rightarrow MI=2\)\(\Rightarrow M\in \left( I;2 \right)\) với \(I=\left( 3;2 \right)\). \(P=\left| z+1-2i \right|+2\left| z-2-5i \right|=MA+2MB\) với \(A=\left( 1;2 \right)\), \(B=\left( 2;5 \right)\).
Ta có \(IM=2\); \(IA=4\). Chọn \(K\left( 2;2 \right)\) thì \(IK=1\). Do đó ta có \(IA.IK=I{{M}^{2}}\)\(\Rightarrow \dfrac{IA}{IM}=\dfrac{IM}{IK}\) \(\Rightarrow \Delta IAM\) và \(\Delta IMK\) đồng dạng với nhau \(\Rightarrow \dfrac{AM}{MK}=\dfrac{IM}{IK}=2\)\(\Rightarrow AM=2MK\).
Từ đó \(P=MA+2MB\)\(=2\left( MK+MB \right)\)\(\ge 2BK\).
Dấu bằng xảy ra khi và chỉ khi \(M\), \(K\), \(B\) thẳng hàng và \(M\) thuộc đoạn thẳng \(BK\).
Từ đó tìm được \(M=\left( 2;2+\sqrt{3} \right)\).
Cách 3: Gọi \(M\left( a;b \right)\) là điểm biểu diễn số phức \(z=a+bi.\)
Đặt \(I=\left( 3;2 \right)\), \(A\left( -1;2 \right)\) và \(B\left( 2;5 \right)\).
Ta xét bài toán: Tìm điểm M thuộc đường tròn \(\left( C \right)\) có tâm \(I\), bán kính \(R=2\) sao cho biểu thức \(P=MA+2MB\) đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm \(K\left( x;y \right)\) sao cho \(MA=2MK\)\(\forall M\in \left( C \right)\).
Ta có \(MA=2MK\Leftrightarrow M{{A}^{2}}=4M{{K}^{2}}\Leftrightarrow {{\left( \overrightarrow{MI}+\overrightarrow{IA} \right)}^{2}}=4{{\left( \overrightarrow{MI}+\overrightarrow{IK} \right)}^{2}}\) \(\Leftrightarrow M{{I}^{2}}+I{{A}^{2}}+2\overrightarrow{MI}.\overrightarrow{IA}=4\left( M{{I}^{2}}+I{{K}^{2}}+2\overrightarrow{MI}.\overrightarrow{IK} \right)\Leftrightarrow 2\overrightarrow{MI}\left( \overrightarrow{IA}-4\overrightarrow{IK} \right)=3{{R}^{2}}+4I{{K}^{2}}-I{{A}^{2}}\)\(\left( * \right)\). \(\left( * \right)\) luôn đúng \(\forall M\in \left( C \right)\Leftrightarrow \left\{ \begin{align} & \overrightarrow{IA}-4\overrightarrow{IK}=\overrightarrow{0} \\ & 3{{R}^{2}}+4I{{K}^{2}}-I{{A}^{2}}=0 \\ \end{align} \right.\) mà
\(\overrightarrow {IA} - 4\overrightarrow {IK} = \overrightarrow 0 \Leftrightarrow \left\{ \begin{array}{l}
4\left( {x - 3} \right) = - 4\\
4\left( {y - 2} \right) = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 2
\end{array} \right.\)
Thử trực tiếp ta thấy \(K\left( 2;2 \right)\) thỏa mãn \(3{{R}^{2}}+4I{{K}^{2}}-I{{A}^{2}}=0\).
Vì \(B{{I}^{2}}={{1}^{2}}+{{3}^{2}}=10>{{R}^{2}}=4\) nên \(B\) nằm ngoài \(\left( C \right)\).
Vì \(K{{I}^{2}}=1<{{R}^{2}}=4\) nên \(K\) nằm trong \(\left( C \right)\).
Ta có \(MA+2MB=2MK+2MB=2\left( MK+MB \right)\ge 2KB\).
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi \(M\) thuộc đoạn thẳng \(BK\).
Do đó \(MA+2MB\) nhỏ nhất khi và chỉ khi M là giao điểm của \(\left( C \right)\) và đoạn thẳng \(BK.\)
Phương trình đường thẳng \(BK:x=2\).
Phương trình đường tròn \(\left( C \right):{{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4\).
Tọa độ điểm \(M\) là nghiệm của hệ
\(\left\{ \begin{array}{l}
x = 2\\
{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 2 + \sqrt 3
\end{array} \right.\) hoặc \(\left\{ \begin{align} & x=2 \\ & y=2-\sqrt{3} \\ \end{align} \right.\).
Thử lại thấy \(M\left( 2;2+\sqrt{3} \right)\) thuộc đoạn \(BK\).
Vậy \(a=2\), \(b=2+\sqrt{3}\) \(\Rightarrow a+b=4+\sqrt{3}\).

Ta có: \(\left| {4{z_1}{z_2} + 16{z_2}{z_3} + 9{z_1}{z_3}} \right| = \left| {{z_3}.\overline {{z_3}} .{z_1}{z_2} + {z_1}.\overline {{z_1}} .{z_2}{z_3} + {z_2}.\overline {{z_2}} .{z_1}{z_3}} \right| = \left| {{z_1}{z_2}{z_3}.\left( {\overline {{z_1}}  + \overline {{z_2}}  + \overline {{z_3}} } \right)} \right| = \left| {{z_1}{z_2}{z_3}} \right|.\left| {\overline {{z_1}}  + \overline {{z_2}}  + \overline {{z_3}} } \right|\)

\( = \left| {{z_1}} \right|.\left| {{z_2}} \right|.\left| {{z_2}} \right|.\left| {\overline {{z_1} + {z_2} + {z_3}} } \right| = 24.\left| {{z_1} + {z_2} + {z_3}} \right| = 48\)

\( \Rightarrow P = \left| {{z_1} + {z_2} + {z_3}} \right| = \dfrac{{48}}{{24}} = 2\)

Ta có \(5w=\left( 2+i \right)\left( z-4 \right)\Leftrightarrow 5w+5i=\left( 2+i \right)z-8+i\Leftrightarrow 5\left| w+i \right|=\left| \left( 2+i \right)z-8+i \right|\)
\(\Leftrightarrow \left| \left( 2+i \right)z-8+i \right|=3\sqrt{5}\Leftrightarrow \left| 2+i \right|.\left| z-\dfrac{8-i}{2+i} \right|=3\sqrt{5}\Leftrightarrow \left| z-\dfrac{8-i}{2+i} \right|=3\Leftrightarrow \left| z-3+2i \right|=3\)
\(\Rightarrow \)Tập hợp điểm \(M\left( z \right)\) là đường tròn \(\left( C \right):{{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9,\) tâm \(I\left( 3;-\,2 \right),\,\,R=3.\)
Gọi \(A\left( 1;2 \right),\,\,B\left( 5;2 \right)\) và \(E\left( 3;2 \right)\) là trung điểm của \(AB\) suy ra \(P=MA+MB\).
Lại có \({{\left( MA+MB \right)}^{2}}\le 2\left( M{{A}^{2}}+M{{B}^{2}} \right)=4.M{{E}^{2}}+A{{B}^{2}}\)\(\Rightarrow \,\,P\) lớn nhất \(\Leftrightarrow \)\(ME\) lớn nhất.
Mà \(IE=4>R=3\)\(\xrightarrow{{}}\,\,M{{E}_{\max }}=IE+R=7.\) Vậy \({{P}_{\max }}=\sqrt{4.M{{E}^{2}}+A{{B}^{2}}}=2\sqrt{53}.\)

Gọi \(z = x + yi\,\,\left( {x,y \in R} \right)\). Từ giả thiết \(\left| {z + 2} \right| = \left| {z + 2i} \right|\)
\(\begin{array}{l} \Rightarrow \left| {x + yi + 2} \right| = \left| {x + yi + 2i} \right| \Leftrightarrow {\left( {x + 2} \right)^2} + {y^2} = {x^2} + {\left( {y + 2} \right)^2} \Leftrightarrow x = y \Leftrightarrow z = x + xi\\ \Rightarrow P = \left| {x + xi - 1 - 2i} \right| + \left| {x + xi - 3 - 4i} \right| + \left| {x + xi - 5 - 6i} \right|\\ = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {x - 2} \right)}^2}} + \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {x - 4} \right)}^2}} + \sqrt {{{\left( {x - 5} \right)}^2} + {{\left( {x - 6} \right)}^2}} \end{array}\)
Sử dụng BĐT \(\sqrt {{a^2} + {b^2}} + \sqrt {{c^2} + {d^2}} \ge \sqrt {{{\left( {a + c} \right)}^2} + {{\left( {b + d} \right)}^2}} \).
Dấu bằng xảy ra \( \Leftrightarrow \dfrac{a}{c} = \dfrac{b}{d}\). Ta có :
\(\begin{array}{l}\sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {x - 2} \right)}^2}} + \sqrt {{{\left( {x - 5} \right)}^2} + {{\left( {x - 6} \right)}^2}} = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {x - 2} \right)}^2}} + \sqrt {{{\left( {5 - x} \right)}^2} + {{\left( {6 - x} \right)}^2}} \\ \ge \sqrt {{{\left( {x - 1 + 6 - x} \right)}^2} + {{\left( {x - 2 + 5 - x} \right)}^2}} = \sqrt {34} \end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \dfrac{{x - 1}}{{6 - x}} = \dfrac{{x - 2}}{{5 - x}} \Leftrightarrow x = \dfrac{7}{2}\).
Mặt khác \(\sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {x - 4} \right)}^2}} = \sqrt {2{x^2} - 14x + 25} = \sqrt 2 \sqrt {{{\left( {x - \dfrac{7}{2}} \right)}^2} + \dfrac{1}{4}} \ge \dfrac{1}{{\sqrt 2 }}\)
Dấu bằng xảy ra \( \Leftrightarrow x = \dfrac{7}{2}\).
Từ đó ta thấy \({P_{\min }} = \dfrac{1}{{\sqrt 2 }} + \sqrt {34} = \dfrac{{1 + 2\sqrt {17} }}{{\sqrt 2 }} \Leftrightarrow a = 1,\,\,b = 2 \Rightarrow a + b = 3\)

Đặt \(\left\{ \begin{array}{l}u = 3iz\\v = - \,2w\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = \dfrac{u}{{3i}}\\w = - \dfrac{v}{2}\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}\left| {z - 5 + 3i} \right| = 3\\\left| {iw + 4 + 2i} \right| = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {\dfrac{u}{{3i}} - 5 + 3i} \right| = 3\\\left| { - \dfrac{{iv}}{2} + 4 + 2i} \right| = 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left| {\dfrac{{u - 9 - 15i}}{{3i}}} \right| = 3\\\left| {\dfrac{{iv - 8 - 4i}}{2}} \right| = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left| {u - 9 - 15i} \right| = 9\\\left| {iv - 8 - 4i} \right| = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {u - 9 - 15i} \right| = 9\\\left| {v - 4 + 8i} \right| = 4\end{array} \right.\).
Do đó, tập hợp điểm \(M\) biểu diễn số phức \(u\) thuộc đường tròn \(\left( {{C}_{1}} \right):{{\left( x-9 \right)}^{2}}+{{\left( y-15 \right)}^{2}}=81.\)
Tập hợp điểm \(N\) biểu diễn số phức \(v\) thuộc đường tròn \(\left( {{C}_{2}} \right):{{\left( x-4 \right)}^{2}}+{{\left( y+8 \right)}^{2}}=16.\)
Xét \(\left( {{C}_{1}} \right)\) có tâm \({{I}_{1}}\left( 9;15 \right),\) bán kính \({R_1} = 9;\) \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {4; - \,8} \right),\) bán kính \({{R}_{2}}=4.\)
Dễ thấy \(\left( {{C}_{1}} \right),\,\,\left( {{C}_{2}} \right)\) không cắt nhau \(\Rightarrow \,\,\left| u-v \right|=MN\) lớn nhất \( \Leftrightarrow \,\,MN = {I_1}{I_2} + {R_1} + {R_2} = \sqrt {554} + 13.\)
Vậy \(T=\left| 3iz+2w \right|\) đạt giá trị lớn nhất bằng \(\sqrt{554}+13.\)

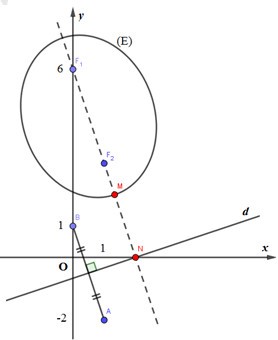
Ta có: \(3\left| {u - 6i} \right| + 3\left| {u - 1 - 3i} \right| = 5\sqrt {10}  \Leftrightarrow \left| {u - 6i} \right| + \left| {u - 1 - 3i} \right| = \dfrac{{5\sqrt {10} }}{3} \Rightarrow \) Tập hợp điểm biểu diễn của số phức \(u\) là đường elip \(\left( E \right)\) có 2 tiêu điểm là \({F_1}(0;6),\,\,{F_2}(1;3)\) và độ dài trục lớn là \(\dfrac{{5\sqrt {10} }}{6}\).

Ta có:  \(\left| {v - 1 + 2i} \right| = \left| {\overline v  + i} \right| = \left| {\overline v  + \left( {\overline { - i} } \right)} \right| = \left| {\overline {v - i} } \right| = \left| {v - i} \right| \Rightarrow \) Tập hợp điểm biểu diễn của số phức \(u\) là đường trung trực \((d)\) của đoạn thẳng AB, trong đó \(A(1; - 2),\,\,B(0;1)\).

Giả sử \(M',\,\,N'\) lần lượt là điểm biểu diễn số phức \(u,\,\,v\) \( \Rightarrow M' \in (E),\,\,N' \in d\)

Nhận xét: Việc tìm GTNN của \(\left| {u - v} \right|\) là tìm độ dài ngắn nhất của đoạn thẳng \(M'N'\).

Dễ dàng kiểm tra được: \({F_1}{F_2} \bot d\)

Gọi \(N = {F_1}{F_2} \cap d,\,\,\,M = {F_1}{F_2} \cap \left( E \right),\,\,(M\)nằm giữa N và \({F_2}\)). Khi đó với mọi điểm \(M' \in (E),\,\,N' \in d\) thì \(MN \le M'N'\)

\( \Rightarrow {\left| {u - v} \right|_{\min }} = MN\)

Ta tính MN ?

+) Viết phương trình đường thẳng d:

\(A(1; - 2),\,\,B(0;1) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB}  = \left( { - 1;3} \right)\\I\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\end{array} \right.\) (I là trung điểm của AB) \( \Rightarrow d:\,\,(x - \dfrac{1}{2}) - 3(y + \dfrac{1}{2}) = 0 \Leftrightarrow x - 3y - 2 = 0\)

+) Phương trình đường thẳng \({F_1}{F_2}\):

\(\overrightarrow {{F_1}{F_2}}  = (1; - 3)\)

\(EF:\,\,\,\,3(x - 0) + 1(y - 6) = 0 \Leftrightarrow 3x + y - 6 = 0\)

+) Tọa độ điểm N là nghiệm của hệ phương trình:  \(\left\{ \begin{array}{l}x - 3y - 2 = 0\\3x + y - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow N(2;0)\)

+) \(M \in {F_1}{F_2} \Rightarrow M(m;6 - 3m),\,\,1 < m < 2\)

Ta có: \(MA + MB = 2a \Leftrightarrow \sqrt {{{\left( {m - 1} \right)}^2} + {{\left( {8 - 3m} \right)}^2}}  + \sqrt {{m^2} + {{(5 - 3m)}^2}}  = \dfrac{{5\sqrt {10} }}{3} \Leftrightarrow m = \dfrac{4}{3} \Rightarrow M\left( {\dfrac{4}{3};2} \right)\)

Suy ra,  \(MN = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2} + {2^2}}  = \dfrac{{2\sqrt {10} }}{3}\) \( \Rightarrow {\left| {u - v} \right|_{\min }} = MN = \dfrac{{2\sqrt {10} }}{3}\)

Đặt 

\(\left( {z - i} \right)\left( {i + 1} \right) = x + yi \Rightarrow \left[ \begin{array}{l}
z - i = \dfrac{{x + yi}}{{i + 1}}\\
z + i = \dfrac{{x + yi}}{{i + 1}} + 2i = \dfrac{{x + yi - 2 + 2i}}{{i + 1}} = \dfrac{{x - 2 + \left( {y + 2} \right)i}}{{i + 1}}
\end{array} \right.\)

\(\Rightarrow \left[ \begin{align}  & \left| z-i \right|=\dfrac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{\sqrt{2}} \\ & \left| z+i \right|=\dfrac{\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y+2 \right)}^{2}}}}{\sqrt{2}} \\\end{align} \right.\) \(\Rightarrow \dfrac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{\sqrt{2}}+\dfrac{\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y+2 \right)}^{2}}}}{\sqrt{2}}=6\,\,\left( * \right)\)

Gọi \(M\left( x;y \right);\,\,I\left( 2;-2 \right)\)  từ (*) ta có \(\frac{MO}{\sqrt{2}}+\frac{MI}{\sqrt{2}}=6\Leftrightarrow MO+MI=6\sqrt{2}\)

Do đó quỹ tích điểm M là elip nhận O; I là hai tiêu điểm và trục lớn \(2a=6\sqrt{2}\Rightarrow a=3\sqrt{2}\)

\(2c=OI=2\sqrt{2}\Rightarrow c=\sqrt{2}\Rightarrow b=\sqrt{{{a}^{2}}-{{c}^{2}}}=4\)

Vậy diện tích elip là \(S=\pi ab=\pi .4.3\sqrt{2}=12\pi \sqrt{2}\)

Ta có: \(\left| {{z_1} - {z_2}} \right| = \left| {i{z_2} - {z_2}} \right| = \left| {{z_2}\left( {1 - i} \right)} \right| = \sqrt 2 \left| {{z_1}} \right|\)

Mà \(\left| {{z_1}} \right| - \left| {1 - i} \right| \le \left| {{z_1} + 1 - i} \right| \le \left| {{z_1}} \right| + \left| {1 - i} \right|\)\( \Rightarrow \left| {{z_1}} \right| - \sqrt 2  \le 2 \le \left| {{z_1}} \right| + \sqrt 2 \)\( \Rightarrow 2 - \sqrt 2  \le \left| {{z_1}} \right| \le 2 + \sqrt 2 \)

\( \Rightarrow \sqrt 2 \left( {2 - \sqrt 2 } \right) \le \sqrt 2 \left| {{z_1}} \right| \le \sqrt 2 \left( {2 + \sqrt 2 } \right)\)\( \Rightarrow 2\sqrt 2  - 2 \le \sqrt 2 \left| {{z_1}} \right| \le 2\sqrt 2  + 2\)

Vậy \(m = 2\sqrt 2  - 2\).

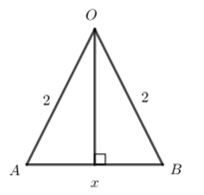
Ta có \(\left| {{z}_{2}} \right|=\left| {{z}_{1}} \right|\left| {{z}_{3}} \right|=2\Rightarrow OB=OA=2\)
Đặt \(AB=x\,\,\left( 0<x<4 \right)\) ta có: \(a=\dfrac{1}{2}.x.\sqrt{4-\dfrac{{{x}^{2}}}{4}}=\dfrac{1}{4}x\sqrt{16-{{x}^{2}}};\,\,b=2+2+x=4+x\)
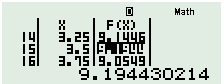
\(\Rightarrow T=a+b=\dfrac{x\sqrt{16-{{x}^{2}}}}{4}+4+x\)
Sử dụng MTCT ta tính được \({{T}_{\max }}\approx 9,19\)

Ta có \(OM=3;\,\,ON=4\) ; \(\widehat{\left( \overrightarrow{OM};\overrightarrow{ON} \right)}={{60}^{0}}\Rightarrow \widehat{\left( OM;ON \right)}={{60}^{0}}\)
\(\left| z \right|=\dfrac{\left| {{z}_{1}}+{{z}_{2}} \right|}{\left| {{z}_{1}}-{{z}_{2}} \right|}=\dfrac{\left| \overrightarrow{OM}+\overrightarrow{ON} \right|}{\left| \overrightarrow{OM}-\overrightarrow{ON} \right|}=\dfrac{2\left| \overrightarrow{OI} \right|}{\left| \overrightarrow{MN} \right|}=\dfrac{2OI}{MN}\) (với I là trung điểm của MN).
Áp dụng định lí cosin trong tam giác OMN có \(MN=\sqrt{O{{M}^{2}}+O{{N}^{2}}-2OM.ON.\cos \left( OM;ON \right)}=\sqrt{13}\)
OI là đường trung tuyến của tam giác OMN \(\Rightarrow OI=\sqrt{\dfrac{O{{M}^{2}}+O{{N}^{2}}}{2}-\dfrac{M{{N}^{2}}}{4}}=\dfrac{\sqrt{37}}{2}\)
Vậy \(\left| z \right|=\dfrac{2.\dfrac{\sqrt{37}}{2}}{\sqrt{13}}=\dfrac{\sqrt{481}}{13}\)

\(\begin{array}{l}\left( {2 + i} \right)\left| z \right| = \dfrac{{\sqrt {17} }}{z} + 1 - 3i\\ \Leftrightarrow \left( {2 + i} \right)\left| z \right| - 1 + 3i = \dfrac{{\sqrt {17} }}{z}\\ \Leftrightarrow \left( {2\left| z \right| - 1} \right) + \left( {\left| z \right| + 3} \right)i = \dfrac{{\sqrt {17} }}{z}\\ \Leftrightarrow {\left( {2\left| z \right| - 1} \right)^2} + {\left( {\left| z \right| + 3} \right)^2} = \dfrac{{17}}{{{{\left| z \right|}^2}}}\\ \Leftrightarrow 5{\left| z \right|^4} + 2{\left| z \right|^3} + 10{\left| z \right|^2} - 17 = 0\\ \Leftrightarrow \left( {\left| z \right| - 1} \right)\left( {5{{\left| z \right|}^3} + 7{{\left| z \right|}^2} + 17\left| z \right| + 17} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| z \right| = 1\\5{\left| z \right|^3} + 7{\left| z \right|^2} + 17\left| z \right| + 17 = 0\end{array} \right.\end{array}\)

Phương trình dưới có một nghiệm âm nên loại. Do đó \(\left| z \right| = 1\)
Đặt \(w = x + yi\) ta có:
\(\begin{array}{l}w = \left( {3 - 4i} \right)z - 1 + 2i \Rightarrow \left( {3 - 4i} \right)z = w + 1 - 2i\\ \Leftrightarrow 5\left| z \right| = \left| {w + 1 - 2i} \right| = 5\end{array}\)
Vậy tập hợp các điểm biểu diễn cho số phức \(w = \left( {3 - 4i} \right)z - 1 + 2i\) là đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính \(R = 5\).