Cho số phức \(z\) thỏa mãn \(\left| z \right|\le 2\). GTNN của biểu thức \(P=2\left| z+1 \right|+2\left| z-1 \right|+\left| z-\overline{z}-4i \right|\) bằng

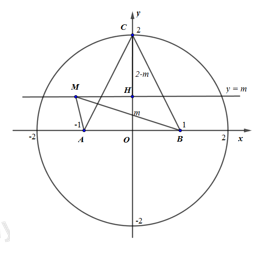
Giả sử \(z=x+yi,\,\,\left( x,y\in R \right)\Rightarrow M(x;y)\) là điểm biểu diễn của \(z\)trên mặt phẳng tọa độ Oxy.

\(P=2\left| z+1 \right|+2\left| z-1 \right|+\left| z-\overline{z}-4i \right|=2\left( \sqrt{{{(x+1)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\left| y-2 \right| \right)\)

Đặt \(A(-1;0),\,\,B(1;0),\,\,C(0;2)\) và \(H(0;y)\) là hình chiếu của M lên Oy. Khi đó, \(P=2\left( MA+MB+HC \right)\)

Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, ( M di chuyển trên hình tròn \({{x}^{2}}+{{y}^{2}}\le 4\))

+) Nếu \(M\in ({{C}_{1}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y<0\)thì ta luôn tìm được điểm \(M'\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\) đối xứng với \(M\)qua Ox. Khi đó

\(P=2\left( MA+MB+HC \right)=2\left( M'A+M'B+H'C \right)>2\left( MA+MB+HC \right)\)

+) Ta xét điểm \(M\in ({{C}_{2}}):{{x}^{2}}+{{y}^{2}}\le 4,\,\,y\ge 0\)

Với M nằm trong nửa hình tròn \(({{C}_{2}})\), thay đổi trên đường thẳng \(y=m\) cố định \(\left( 0\le m\le 2 \right)\) thì độ dài đoạn HC không đổi, \(MA+MB\ge HA+HB=2HA\)

\(P=2\left( MA+MB+HC \right)\ge 2\left( 2HA+HC \right)\)

Ta có: \(2HA+HC=2\sqrt{{{m}^{2}}+1}+2-m=f(m),\,\,m\in \left[ 0;2 \right]\)

\(f'(m)=\dfrac{2}{\sqrt{{{m}^{2}}+1}}-1,\,\,\,f'(m)=0\Leftrightarrow m=\dfrac{1}{\sqrt{3}}\)

\(f{{(m)}_{\min }}=f\left( \dfrac{1}{\sqrt{3}} \right)=1+\dfrac{\sqrt{3}}{2}\)

 \(\Rightarrow {{P}_{\min }}=2\left( 1+\dfrac{\sqrt{3}}{2} \right)=2+\sqrt{3}\) khi \(M\left( 0;\dfrac{1}{\sqrt{3}} \right)\,\,hay\,\,z=\dfrac{i}{\sqrt{3}}\) .