Cho \({{z}_{1}};{{z}_{2}};{{z}_{3}}\) là ba số phức thay đổi thỏa mãn \(\left| {{z}_{1}} \right|=2;\,\,\left| {{z}_{3}} \right|=1\) và \({{z}_{2}}={{z}_{1}}{{z}_{3}}\) Trong mặt phẳng phức A, B biểu diễn \({{z}_{1}};{{z}_{2}}\) Giả sử O, A, B lập thành tam giác có diện tích là a, chu vi là b. Giá trị lớn nhất của biểu thức \(T=a+b\) là:
Trả lời bởi giáo viên
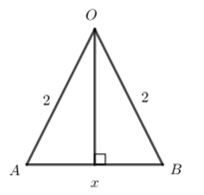
Ta có \(\left| {{z}_{2}} \right|=\left| {{z}_{1}} \right|\left| {{z}_{3}} \right|=2\Rightarrow OB=OA=2\)
Đặt \(AB=x\,\,\left( 0<x<4 \right)\) ta có: \(a=\dfrac{1}{2}.x.\sqrt{4-\dfrac{{{x}^{2}}}{4}}=\dfrac{1}{4}x\sqrt{16-{{x}^{2}}};\,\,b=2+2+x=4+x\)
\(\Rightarrow T=a+b=\dfrac{x\sqrt{16-{{x}^{2}}}}{4}+4+x\)
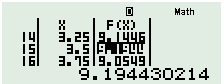
Sử dụng MTCT ta tính được \({{T}_{\max }}\approx 9,19\)
Hướng dẫn giải:
+) Đặt \(AB=x\,\,\left( 0<x<4 \right)\) Tính diện tích và chu vi tam giác OAB theo x.
+) Viết \(T=f\left( x \right)\) Tìm GTLN của \(f\left( x \right)\)

