Cho hai số phức $u,\,\,v$ thỏa mãn $3\left| {u - 6i} \right| + 3\left| {u - 1 - 3i} \right| = 5\sqrt {10} ,\,\,\left| {v - 1 + 2i} \right| = \left| {\overline v  + i} \right|$. GTNN của $\left| {u - v} \right|$ là

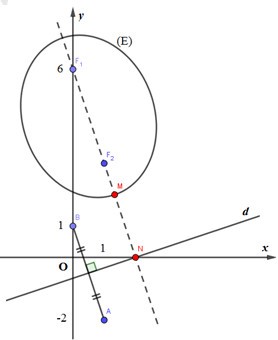
Ta có: $3\left| {u - 6i} \right| + 3\left| {u - 1 - 3i} \right| = 5\sqrt {10}  \Leftrightarrow \left| {u - 6i} \right| + \left| {u - 1 - 3i} \right| = \dfrac{{5\sqrt {10} }}{3} \Rightarrow$ Tập hợp điểm biểu diễn của số phức $u$ là đường elip $\left( E \right)$ có 2 tiêu điểm là ${F_1}(0;6),\,\,{F_2}(1;3)$ và độ dài trục lớn là $\dfrac{{5\sqrt {10} }}{6}$.

Ta có:  $\left| {v - 1 + 2i} \right| = \left| {\overline v  + i} \right| = \left| {\overline v  + \left( {\overline { - i} } \right)} \right| = \left| {\overline {v - i} } \right| = \left| {v - i} \right| \Rightarrow$ Tập hợp điểm biểu diễn của số phức $u$ là đường trung trực $(d)$ của đoạn thẳng AB, trong đó $A(1; - 2),\,\,B(0;1)$.

Giả sử $M',\,\,N'$ lần lượt là điểm biểu diễn số phức $u,\,\,v$ $\Rightarrow M' \in (E),\,\,N' \in d$

Nhận xét: Việc tìm GTNN của $\left| {u - v} \right|$ là tìm độ dài ngắn nhất của đoạn thẳng $M'N'$.

Dễ dàng kiểm tra được: ${F_1}{F_2} \bot d$

Gọi $N = {F_1}{F_2} \cap d,\,\,\,M = {F_1}{F_2} \cap \left( E \right),\,\,(M$nằm giữa N và ${F_2}$). Khi đó với mọi điểm $M' \in (E),\,\,N' \in d$ thì $MN \le M'N'$

$\Rightarrow {\left| {u - v} \right|_{\min }} = MN$

Ta tính MN ?

+) Viết phương trình đường thẳng d:

$A(1; - 2),\,\,B(0;1) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB}  = \left( { - 1;3} \right)\\I\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\end{array} \right.$ (I là trung điểm của AB) $\Rightarrow d:\,\,(x - \dfrac{1}{2}) - 3(y + \dfrac{1}{2}) = 0 \Leftrightarrow x - 3y - 2 = 0$

+) Phương trình đường thẳng ${F_1}{F_2}$:

$\overrightarrow {{F_1}{F_2}}  = (1; - 3)$

$EF:\,\,\,\,3(x - 0) + 1(y - 6) = 0 \Leftrightarrow 3x + y - 6 = 0$

+) Tọa độ điểm N là nghiệm của hệ phương trình:  $\left\{ \begin{array}{l}x - 3y - 2 = 0\\3x + y - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow N(2;0)$

+) $M \in {F_1}{F_2} \Rightarrow M(m;6 - 3m),\,\,1 < m < 2$

Ta có: $MA + MB = 2a \Leftrightarrow \sqrt {{{\left( {m - 1} \right)}^2} + {{\left( {8 - 3m} \right)}^2}}  + \sqrt {{m^2} + {{(5 - 3m)}^2}}  = \dfrac{{5\sqrt {10} }}{3} \Leftrightarrow m = \dfrac{4}{3} \Rightarrow M\left( {\dfrac{4}{3};2} \right)$

Suy ra,  $MN = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2} + {2^2}}  = \dfrac{{2\sqrt {10} }}{3}$ $\Rightarrow {\left| {u - v} \right|_{\min }} = MN = \dfrac{{2\sqrt {10} }}{3}$