Tổng hợp câu hay và khó chương 7 phần 2

Giả sử \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\), ta có: \(OA = \left| a \right|;\,\,OB = \left| b \right|;\,\,OC = \left| c \right|\)

\(OA = OB = OC \ne 0 \Leftrightarrow \left| a \right| = \left| b \right| = \left| c \right| \ne 0\)

TH1: \(a = b = c \Rightarrow \left( P \right):\,\,\dfrac{x}{a} + \dfrac{y}{a} + \dfrac{z}{a} = 1 \Leftrightarrow x + y + z - a = 0\)

\(M \in \left( {ABC} \right) \Rightarrow 2 - a = 0 \Leftrightarrow a = 2 \Rightarrow \left( P \right):\,\,x + y + z - 2 = 0\)

TH2: \(a = b =  - c \Leftrightarrow \left( P \right):\,\,\dfrac{x}{a} + \dfrac{y}{a} + \dfrac{z}{{ - a}} = 1 \Leftrightarrow x + y - z - a = 0\)

\(M \in \left( {ABC} \right) \Rightarrow 6 - a = 0 \Leftrightarrow a = 6 \Rightarrow \left( P \right):\,\,x + y - z - 6 = 0\)

TH3: \(a =  - b = c \Leftrightarrow \left( P \right):\,\,\dfrac{x}{a} + \dfrac{y}{{ - a}} + \dfrac{z}{a} = 1 \Leftrightarrow x - y + z - a = 0\)

\(M \in \left( {ABC} \right) \Rightarrow  - 4 - a = 0 \Leftrightarrow a =  - 4 \Rightarrow \left( P \right):\,\,x - y + z + 4 = 0\)

TH4: \( - a = b = c \Rightarrow \left( P \right):\,\,\dfrac{x}{a} + \dfrac{y}{{ - a}} + \dfrac{z}{{ - a}} = 1 \Leftrightarrow x - y - z - a = 0\)

\(M \in \left( {ABC} \right) \Rightarrow 0 - a = 0 \Leftrightarrow a = 0\) => Loại.

Vậy có 3 mặt phẳng thỏa mãn yêu cầu bài toán.

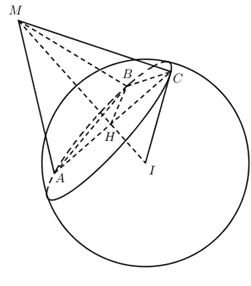
Mặt cầu (S) có tâm \(I\left( {1;2; - 3} \right)\), bán kính \(R = 3\sqrt 3 \).

Đặt \(MA = MB = MC = a\).

Tam giác \(MAB\) đều \( \Rightarrow AB = a\)

Tam giác \(MBC\) vuông tại M \( \Rightarrow BC = a\sqrt 2 \)

Tam giác \(MCA\) có \(\widehat {CMA} = {120^0} \Rightarrow AC = a\sqrt 3 \)

Xét tam giác \(ABC\) có \(A{B^2} + B{C^2} = A{C^2} \Rightarrow \Delta ABC\) vuông tại B \( \Rightarrow \Delta ABC\) ngoại tiếp đường tròn nhỏ có đường kính \(AC\)\( \Rightarrow HA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 3 }}{2}\)

Xét tam giác vuông \(IAM\) có:

\(\dfrac{1}{{H{A^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{I{A^2}}} \Rightarrow \dfrac{4}{{3{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{27}} \Leftrightarrow \dfrac{1}{{3{a^2}}} = \dfrac{1}{{27}} \Leftrightarrow a = 3 = MA\)

\( \Rightarrow I{M^2} = M{A^2} + I{A^2} = {3^2} + 27 = 36\)

\(\begin{array}{l}M \in \left( d \right) \Rightarrow M\left( { - 1 + t; - 2 + t;1 + t} \right) \Leftrightarrow I{M^2} = {\left( {t - 2} \right)^2} + {\left( {t - 4} \right)^2} + {\left( {t + 4} \right)^2} = 36\\ \Leftrightarrow 3{t^2} - 4t = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \dfrac{4}{3}\end{array} \right. \Rightarrow \left[ \begin{array}{l}M\left( { - 1; - 2;1} \right)\\M\left( {\dfrac{1}{3}; - \dfrac{2}{3};\dfrac{7}{3}} \right)\,\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 2\\c = 1\end{array} \right. \Rightarrow a + b + c =  - 2\end{array}\)

Gọi $H\left( {1 + 2t; - 1 + t;2 - t} \right) \in d$ là hình chiếu của $A$ trên $d$

Ta có $\overrightarrow {AH}  = \left( {2t; - \,3 + t;3 - t} \right),$ khi đó $\overrightarrow {AH} .\overrightarrow {{u_d}}  = 0 \Leftrightarrow 4t + t - 3 + t - 3 = 0 \Leftrightarrow t = 1.$

Suy ra $H\left( {3;0;1} \right) \Rightarrow $ Phương trình đường thẳng $AH$ là $\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{{ - \,1}} = \dfrac{{z + 1}}{1}.$

Do đó $B = AH \cap \left( P \right)$ suy ra $B\left( {0;3; - \,2} \right).$

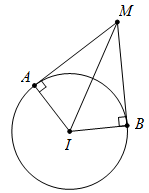
Xét $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 6$ có tâm $I\left( {1;2; - \,1} \right),$ bán kính $R = \sqrt 6 .$

Gọi $M$ là giao điểm của $\left( P \right)$ và $\left( Q \right)$ sao cho $MAIB$ đồng phẳng.

Ta có $\cos \widehat {AMB} = \cos \widehat {\left( P \right);\left( Q \right)} = \dfrac{{\left| {{{\vec n}_{\left( P \right)}}.{{\vec n}_{\left( Q \right)}}} \right|}}{{\left| {{{\vec n}_{\left( P \right)}}} \right|.\left| {{{\vec n}_{\left( Q \right)}}} \right|}} = \dfrac{1}{2} \Rightarrow \,\,\widehat {AMB} = {60^0} \Rightarrow \,\,\widehat {AIB} = {120^0}.$

Tam giác $IAB$ cân tại $I,$ có $AB = \sqrt {I{A^2} + I{B^2} - 2.IA.IB.\cos \widehat {AIB}}  = 3\sqrt 2 .$

Để $AB$ nhỏ nhất $ \Leftrightarrow \,\,AB$ là đoạn vuông góc chung của $d,\,\,d'.$

Gọi $A \in d \Rightarrow \,\,A\left( {1 + a;2 - a;a} \right)$ và $B \in d' \Rightarrow \,\,B\left( {2b;1 + b;2 + b} \right)$$ \Rightarrow $$\overrightarrow {AB}  = \left( {2b - a - 1;a + b - 1;b - a + 2} \right).$

Vì $\left\{ \begin{array}{l}AB \bot d\\AB \bot d'\end{array} \right. \Rightarrow \,\,\left\{ \begin{array}{l}\overrightarrow {AB} .{{\vec u}_d} = 0\\\overrightarrow {AB} .{{\vec u}_{d'}} = 0\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}2b - a - 1 - a - b + 1 + b - a + 2 = 0\\2\left( {2b - a - 1} \right) + a + b - 1 + b - a + 2 = 0\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l} - \,3a + 2b + 2 = 0\\ - \,2a + 6b - 1 = 0\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}a = 1\\b = \dfrac{1}{2}\end{array} \right..$

Vậy $A\left( {2;1;1} \right),\,\,B\left( {1;\dfrac{3}{2};\dfrac{5}{2}} \right) \Rightarrow \,\,\overrightarrow {AB}  = \left( { - \,1;\dfrac{1}{2};\dfrac{3}{2}} \right) =  - \,\dfrac{1}{2}\left( {2; - \,1; - \,3} \right) \Rightarrow \,\,\left( {AB} \right):\dfrac{{x - 2}}{{ - \,2}} = \dfrac{{y - 1}}{1} = \dfrac{{z - 1}}{3}.$

Ta có $E{F_{\max }} \Leftrightarrow d{\left( {I;\left( d \right)} \right)_{\min }} = \dfrac{{\left| {\left[ {\overrightarrow {I{M_0}} ;\overrightarrow {{u_d}} } \right]} \right|}}{{\left| {\overrightarrow {{u_d}} } \right|}}{\;_{\min }}$ (trong đó điểm ${M_0}\left( {1; - 1;m} \right)$)

Ta có: $d\left( {I;\left( d \right)} \right) = \dfrac{{\left| {\left[ {\overrightarrow {I{M_0}} ;\overrightarrow {{u_d}} } \right]} \right|}}{{\left| {\overrightarrow {{u_d}} } \right|}}\; = \dfrac{{\sqrt {{{\left( {m + 2} \right)}^2} + {{\left( {m - 2} \right)}^2} + 4} }}{{\sqrt {1 + 1 + 4} }} = \dfrac{{\sqrt {2{m^2} + 12} }}{{\sqrt 6 }}$

Vì $2{m^2} \ge 0$ suy ra $d\left( {I;\left( d \right)} \right) \le \dfrac{{\sqrt {12} }}{{\sqrt 6 }} = \sqrt 2  \Rightarrow \,\,{d_{\min }} = \sqrt 2  < R = 3$ khi $m = 0.$

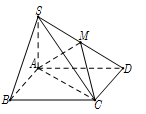
Gắn hệ tọa độ $Oxyz,$ với $A\left( {0;0;0} \right),\,\,S\left( {0;0;2} \right),\,\,D\left( {0;1;0} \right),\,\,B\left( {1;0;0} \right),\,\,C\left( {1;1;0} \right)$.

Tọa độ trung điểm $M$ của $SD$ là $M\left( {0;\dfrac{1}{2};1} \right).$

$\overrightarrow {SB} = \left( {1;0; - 2} \right),\overrightarrow {SC} = \left( {1;1; - 2} \right)$

Ta có $\left[ {\overrightarrow {SB} ;\overrightarrow {SC} } \right] = \left( {2;0;1} \right)$

$\overrightarrow {AM} = \left( {0;\frac{1}{2};1} \right),\overrightarrow {AC} = \left( {1;1;0} \right)$

$\left[ {\overrightarrow {AM} ;\overrightarrow {AC} } \right] = \left( { - \,1;1; - \,\dfrac{1}{2}} \right).$

Do đó

$\cos (\widehat {\left( {AMC} \right);\left( {SBC} \right)}) = \dfrac{{\left| {{{\vec n}_{\left( {AMC} \right)}}.{{\vec n}_{\left( {SBC} \right)}}} \right|}}{{\left| {{{\vec n}_{\left( {AMC} \right)}}} \right|.\left| {.{{\vec n}_{\left( {SBC} \right)}}} \right|}}  $

$ = \frac{{\left| {2.\left( { - 1} \right) + 0.1 + 1.\left( { - \frac{1}{2}} \right)} \right|}}{{\sqrt {{2^2} + {0^2} + {1^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {1^2} + {{\left( { - \frac{1}{2}} \right)}^2}} }} = \frac{{\sqrt 5 }}{3}$

$ \Rightarrow \tan \left( {\widehat {\left( {AMC} \right),\left( {SBC} \right)}} \right) = \sqrt {\frac{1}{{{{\left( {\frac{{\sqrt 5 }}{3}} \right)}^2}}} - 1} = \frac{{2\sqrt 5 }}{5}$

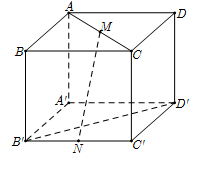
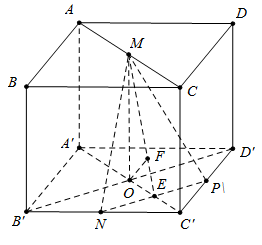
Cách 1: Chọn hệ trục tọa độ với $A'\left( {0;0;0} \right)$

$\begin{array}{l}B'\left( {1;0;0} \right);D'\left( {0;1;0} \right);A\left( {0;0;1} \right),\,\,C\left( {1;1;1} \right);\,\,C'\left( {1;1;0} \right);\,\,\\B\left( {1;0;1} \right);\,\,D\left( {0;1;1} \right)\end{array}$

Ta có: $M\left( {\dfrac{1}{2};\dfrac{1}{2};1} \right);N\left( {1;\dfrac{1}{2};0} \right)$

Khi đó $\overrightarrow {B'D'}  = \left( { - 1;1;0} \right);\overrightarrow {MN}  = \left( {\dfrac{1}{2};0; - 1} \right)$

Suy ra $\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right] = \left( { - 1; - 1;\dfrac{{ - 1}}{2}} \right)$

\(\overrightarrow {NB'}  = \left( {0;\dfrac{1}{2};0} \right) \Rightarrow \left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right].\overrightarrow {NB'}  =  - \dfrac{1}{2}\)

\( \Rightarrow d\left( {MN;B'D'} \right) = \dfrac{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right].\overrightarrow {NB'} } \right|}}{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right]} \right|}} = \dfrac{{\dfrac{1}{2}}}{{\dfrac{3}{2}}} = \dfrac{1}{3}\)

Cách 2: Gọi P là trung điểm của $C'D'$ suy ra $d = d\left( {O;\left( {MNP} \right)} \right)$

Dựng $OE \bot NP;\;OF \bot ME \Rightarrow d = OF = \dfrac{{MO.OE}}{{\sqrt {M{O^2} + O{E^2}} }}$ trong đó $MO = a;OE = \dfrac{{a\sqrt 2 }}{4} \Rightarrow d = \dfrac{a}{3}.$

Gọi $A\left( {0;0;a} \right)\,\,\left( {a > 0} \right),$ vì $AB \bot \,\,mp\,\,\left( \alpha  \right)$$ \Rightarrow $ Phương trình đường thẳng $\left( {AB} \right):\left\{ \begin{array}{l}x = t\\y = 0\\z = a - t\end{array} \right..$

Mà $B = AB \cap \left( \alpha  \right)$$ \Rightarrow \,\,B\left( {t;0;a - t} \right)$ và $B \in \,\,mp\,\,\left( \alpha  \right)$$ \Rightarrow $$t - \left( {a - t} \right) - 3 = 0 \Leftrightarrow t = \dfrac{{a + 3}}{2}.$

Khi đó $B\left( {\dfrac{{a + 3}}{2};0;\dfrac{{a - 3}}{2}} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AM}  = \left( {1;1;1 - a} \right)\\\overrightarrow {BM}  = \left( { - \dfrac{{a + 1}}{2};1;\dfrac{{5 - a}}{2}} \right)\end{array} \right.$

$\begin{array}{l}AM = BM \Leftrightarrow A{M^2} = B{M^2} \Leftrightarrow 2 + {\left( {1 - a} \right)^2} = 1 + \dfrac{{{{\left( {a + 1} \right)}^2} + {{\left( {5 - a} \right)}^2}}}{4}\\ \Leftrightarrow {a^2} - 2a + 2 = \dfrac{{2{a^2} - 8a + 26}}{4}\\ \Leftrightarrow 2{a^2} = 18 \Leftrightarrow {a^2} = 9 \Leftrightarrow a = 3\,\,\left( {a > 0} \right)\\ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AM}  = \left( {1;1; - 2} \right)\\\overrightarrow {BM}  = \left( { - 2;1;1} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {MA} ;\overrightarrow {MB} } \right] = \left( {3;3;3} \right)\end{array}$

Vậy diện tích tam giác $MAB$ là ${S_{\Delta \,MAB}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {MA} ;\overrightarrow {MB} } \right]} \right| = \dfrac{{3\sqrt 3 }}{2}.$

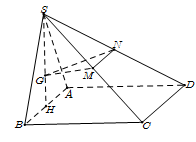
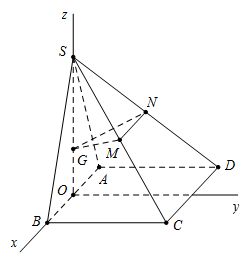
Gọi H là trung điểm của $AB.$ Vì $\left( {SAD} \right) \bot \left( {ABCD} \right)$$ \Rightarrow \,\,SH \bot \left( {ABCD} \right).$

Gắn hệ tọa độ $Oxyz,$ với $H\left( {0;0;0} \right),\,\,S\left( {0;0;\dfrac{{\sqrt 3 }}{2}} \right),\,\,A\left( { - \dfrac{1}{2};0;0} \right);\,\,B\left( {\dfrac{1}{2};0;0} \right);\,\,C\left( {\dfrac{1}{2};1;0} \right),\,\,D\left( { - \dfrac{1}{2};1;0} \right)$

Khi đó $G\left( {0;0;\dfrac{{\sqrt 3 }}{6}} \right),\,\,M\left( {\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{4}} \right),\,\,N\left( { - \,\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{4}} \right)$

$\begin{array}{l} \Rightarrow \overrightarrow {GM}  = \left( {\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{{12}}} \right);\,\,\overrightarrow {MN}  = \left( { - \dfrac{1}{2};0;0} \right)\\ \Rightarrow \,\,{{\vec n}_1} = {{\vec n}_{\left( {GMN} \right)}} = \left[ {\overrightarrow {GM} ;\overrightarrow {MN} } \right] = \left( {0; - \dfrac{{\sqrt 3 }}{{24}};\dfrac{1}{4}} \right).\end{array}$

Và mặt phẳng $\left( {ABCD} \right)$ có vectơ pháp tuyến là ${\vec n_2} = {\vec n_{\left( {ABCD} \right)}} = \overrightarrow k  = \left( {0;0;1} \right).$

Vậy cosin góc giữa hai mặt phẳng $\left( {GMN} \right),\,\,\left( {ABCD} \right)$ là $\cos \alpha  = \dfrac{{\left| {{{\vec n}_1}.{{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right|.\left| {{{\vec n}_2}} \right|}} = \dfrac{{2\sqrt {39} }}{{13}}.$

Gọi $M\left( {x;y;z} \right)$$ \Rightarrow \,\,\overrightarrow {AM}  = \left( {x - 10;y - 6;z + 2} \right);\,\,\overrightarrow {BM}  = \left( {x - 5;y - 10;z + 9} \right)$

Gọi $H,\,\,K$ lần lượt là hình chiếu của $A,\,\,B$ lên $\left( \alpha  \right),$ có $\widehat {AMH} = \widehat {BMK}.$

\(AH = d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {2.10 + 2.6 - 2 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 6;\,\,BK = d\left( {B;\left( P \right)} \right) = \dfrac{{\left| {2.5 + 2.10 - 9 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 3\)

Khi đó $\left\{ \begin{array}{l}\sin \widehat {AMH} = \dfrac{{AH}}{{MA}}\\\sin \widehat {BMK} = \dfrac{{BK}}{{MB}}\end{array} \right. \Rightarrow \dfrac{{AH}}{{MA}} = \dfrac{{BK}}{{MB}} \Rightarrow MA = 2\,MB \Leftrightarrow M{A^2} = 4M{B^2}.$

Suy ra ${\left( {x - 10} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 2} \right)^2} = 4\left[ {{{\left( {x - 5} \right)}^2} + {{\left( {y - 10} \right)}^2} + {{\left( {z + 9} \right)}^2}} \right]$

$ \Leftrightarrow {x^2} + {y^2} + {z^2} - \dfrac{{20}}{3}x - \dfrac{{68}}{3}y + \dfrac{{68}}{3}z + 228 = 0 \Leftrightarrow \left( S \right):{\left( {x - \dfrac{{10}}{3}} \right)^2} + {\left( {y - \dfrac{{34}}{3}} \right)^2} + {\left( {z + \dfrac{{34}}{3}} \right)^2} = 40$ có tâm \(I\left( {\dfrac{{10}}{3};\dfrac{{34}}{3};\dfrac{{ - 34}}{3}} \right)\).

Vậy $M \in \left( C \right)$ là giao tuyến của $\left( \alpha  \right)$ và $\left( S \right) \Rightarrow $ Tâm K của \(\left( C \right)\) là hình chiếu của \(I\left( {\dfrac{{10}}{3};\dfrac{{34}}{3};\dfrac{{ - 34}}{3}} \right)\) trên mặt phẳng \(\left( \alpha  \right)\).

Phương trình đường thẳng đi qua I à vuông góc với \(\left( \alpha  \right)\) có dạng \(\left\{ \begin{array}{l}x = \dfrac{{10}}{3} + 2t\\y = \dfrac{{34}}{3} + 2t\\z =  - \dfrac{{34}}{3} + t\end{array} \right.\)

\(\begin{array}{l} \Rightarrow K\left( {\dfrac{{10}}{3} + 2t;\dfrac{{34}}{3} + 2t; - \dfrac{{34}}{3} + t} \right),\,\,K \in \left( \alpha  \right) \Rightarrow 2\left( {\dfrac{{10}}{3} + 2t} \right) + 2\left( {\dfrac{{34}}{3} + 2t} \right) + \left( { - \dfrac{{34}}{3} + t} \right) - 12 = 0\\ \Leftrightarrow 9t + 6 = 0 \Leftrightarrow t =  - \dfrac{2}{3} \Rightarrow K\left( {2;10; - 12} \right) \Rightarrow {x_K} = 2\end{array}\)

Dễ thấy $d//\left( \alpha  \right)$ và $\left( { - \,1; - \,2; - \,3} \right) \in \left( \alpha  \right)$$ \Rightarrow \,\,d \subset \left( \alpha  \right).$

Ta có $B = \Delta  \cap \left( {Oxy} \right) \Rightarrow B\left( {a;b;0} \right)$ mà $B \in \Delta  \subset \left( \alpha  \right)$$ \Rightarrow \,\,2a + b - 2 = 0 \Rightarrow b = 2 - 2a$

Lại có $d$//$\Delta $$ \Rightarrow \,\,d\left( {\left( d \right);\left( \Delta  \right)} \right) = d\left( {B;\left( d \right)} \right) = 3.$ Đường thẳng $d$ đi qua $M\left( {0;0; - \,1} \right),$ có ${\vec u_d} = \left( {1;2;2} \right).$

\(\overrightarrow {BM}  = \left( { - a; - b; - 1} \right) \Rightarrow \left[ {\overrightarrow {BM} ;\overrightarrow u } \right] = \left( { - 2b + 2; - 1 + 2a; - 2a + b} \right)\)

Do đó

$\begin{array}{l}d\left( {B;\left( d \right)} \right) = \dfrac{{\left| {\left[ {\overrightarrow {BM} ;{{\vec u}_d}} \right]} \right|}}{{\left| {{{\vec u}_d}} \right|}} = \dfrac{{\sqrt {{{\left( {2b - 2} \right)}^2} + {{\left( {1 - 2a} \right)}^2} + {{\left( {2a - b} \right)}^2}} }}{3} = 3\\ \Leftrightarrow {\left( {2b - 2} \right)^2} + {\left( {1 - 2a} \right)^2} + {\left( {2a - b} \right)^2} = 81 \Leftrightarrow {\left( {2 - 4a} \right)^2} + {\left( {1 - 2a} \right)^2} + {\left( {4a - 2} \right)^2} = 81\\ \Leftrightarrow {\left( {1 - 2a} \right)^2} = 9 \Leftrightarrow \left[ \begin{array}{l}1 - 2a = 3\\1 - 2a =  - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a =  - 1\\a = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a =  - 1\\b = 4\end{array} \right. \Rightarrow B\left( { - 1;4;0} \right)\\\left\{ \begin{array}{l}a = 2\\b =  - 2\end{array} \right. \Rightarrow B\left( {2; - 2;0} \right)\end{array} \right.\end{array}$     

Vậy $AB = \dfrac{7}{2}.$