Câu hỏi:
2 năm trước
Trong không gian \(Oxyz,\) cho mặt cầu \((S):{(x - 1)^2} + {(y - 2)^2} + {(z + 1)^2} = 6,\) tiếp xúc với hai mặt phẳng \((P):x + y + 2z\, + \,5 = 0,\,\,(Q):2x - y + z\, - \,5 = 0\) lần lượt tại các tiếp điểm $A,\,\,B.$ Độ dài đoạn thẳng $AB$ là
Trả lời bởi giáo viên
Đáp án đúng: d
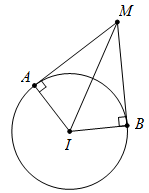
Xét $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 6$ có tâm $I\left( {1;2; - \,1} \right),$ bán kính $R = \sqrt 6 .$
Gọi $M$ là giao điểm của $\left( P \right)$ và $\left( Q \right)$ sao cho $MAIB$ đồng phẳng.
Ta có $\cos \widehat {AMB} = \cos \widehat {\left( P \right);\left( Q \right)} = \dfrac{{\left| {{{\vec n}_{\left( P \right)}}.{{\vec n}_{\left( Q \right)}}} \right|}}{{\left| {{{\vec n}_{\left( P \right)}}} \right|.\left| {{{\vec n}_{\left( Q \right)}}} \right|}} = \dfrac{1}{2} \Rightarrow \,\,\widehat {AMB} = {60^0} \Rightarrow \,\,\widehat {AIB} = {120^0}.$
Tam giác $IAB$ cân tại $I,$ có $AB = \sqrt {I{A^2} + I{B^2} - 2.IA.IB.\cos \widehat {AIB}} = 3\sqrt 2 .$
Hướng dẫn giải:
Đưa về bài toán đường tròn tiếp xúc với hai đường thẳng cắt nhau, sử dụng bài toán hình phẳng lớp 9 để tìm AB thông qua dữ kiện góc
