Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 2x - 4y + 6z - 13 = 0\) và đường thẳng \(d:\,\,\dfrac{{x + 1}}{1} = \dfrac{{y + 2}}{1} = \dfrac{{z - 1}}{1}\). Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn \(\widehat {AMB} = {60^0};\,\,\widehat {BMC} = {90^0};\,\widehat {CMA} = {120^0}\) có dạng \(M\left( {a;b;c} \right)\) với \(a < 0\). Tổng \(a + b + c\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
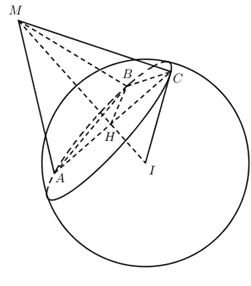
Mặt cầu (S) có tâm \(I\left( {1;2; - 3} \right)\), bán kính \(R = 3\sqrt 3 \).
Đặt \(MA = MB = MC = a\).
Tam giác \(MAB\) đều \( \Rightarrow AB = a\)
Tam giác \(MBC\) vuông tại M \( \Rightarrow BC = a\sqrt 2 \)
Tam giác \(MCA\) có \(\widehat {CMA} = {120^0} \Rightarrow AC = a\sqrt 3 \)
Xét tam giác \(ABC\) có \(A{B^2} + B{C^2} = A{C^2} \Rightarrow \Delta ABC\) vuông tại B \( \Rightarrow \Delta ABC\) ngoại tiếp đường tròn nhỏ có đường kính \(AC\)\( \Rightarrow HA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 3 }}{2}\)
Xét tam giác vuông \(IAM\) có:
\(\dfrac{1}{{H{A^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{I{A^2}}} \Rightarrow \dfrac{4}{{3{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{27}} \Leftrightarrow \dfrac{1}{{3{a^2}}} = \dfrac{1}{{27}} \Leftrightarrow a = 3 = MA\)
\( \Rightarrow I{M^2} = M{A^2} + I{A^2} = {3^2} + 27 = 36\)
\(\begin{array}{l}M \in \left( d \right) \Rightarrow M\left( { - 1 + t; - 2 + t;1 + t} \right) \Leftrightarrow I{M^2} = {\left( {t - 2} \right)^2} + {\left( {t - 4} \right)^2} + {\left( {t + 4} \right)^2} = 36\\ \Leftrightarrow 3{t^2} - 4t = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \dfrac{4}{3}\end{array} \right. \Rightarrow \left[ \begin{array}{l}M\left( { - 1; - 2;1} \right)\\M\left( {\dfrac{1}{3}; - \dfrac{2}{3};\dfrac{7}{3}} \right)\,\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = - 2\\c = 1\end{array} \right. \Rightarrow a + b + c = - 2\end{array}\)
Hướng dẫn giải:
Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.
Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.
