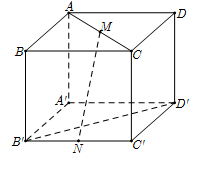
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AC\) và \(B'C'\) (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng \(MN\) và \(B'D'\) bằng
Trả lời bởi giáo viên
Cách 1: Chọn hệ trục tọa độ với $A'\left( {0;0;0} \right)$
$\begin{array}{l}B'\left( {1;0;0} \right);D'\left( {0;1;0} \right);A\left( {0;0;1} \right),\,\,C\left( {1;1;1} \right);\,\,C'\left( {1;1;0} \right);\,\,\\B\left( {1;0;1} \right);\,\,D\left( {0;1;1} \right)\end{array}$
Ta có: $M\left( {\dfrac{1}{2};\dfrac{1}{2};1} \right);N\left( {1;\dfrac{1}{2};0} \right)$
Khi đó $\overrightarrow {B'D'} = \left( { - 1;1;0} \right);\overrightarrow {MN} = \left( {\dfrac{1}{2};0; - 1} \right)$
Suy ra $\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right] = \left( { - 1; - 1;\dfrac{{ - 1}}{2}} \right)$
\(\overrightarrow {NB'} = \left( {0;\dfrac{1}{2};0} \right) \Rightarrow \left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right].\overrightarrow {NB'} = - \dfrac{1}{2}\)
\( \Rightarrow d\left( {MN;B'D'} \right) = \dfrac{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right].\overrightarrow {NB'} } \right|}}{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right]} \right|}} = \dfrac{{\dfrac{1}{2}}}{{\dfrac{3}{2}}} = \dfrac{1}{3}\)
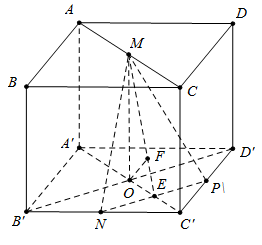
Cách 2: Gọi P là trung điểm của $C'D'$ suy ra $d = d\left( {O;\left( {MNP} \right)} \right)$
Dựng $OE \bot NP;\;OF \bot ME \Rightarrow d = OF = \dfrac{{MO.OE}}{{\sqrt {M{O^2} + O{E^2}} }}$ trong đó $MO = a;OE = \dfrac{{a\sqrt 2 }}{4} \Rightarrow d = \dfrac{a}{3}.$
Hướng dẫn giải:
Cách 1: Gắn hệ trục tọa độ Oxyz sao cho $A'\left( {0;0;0} \right),\,\,B'\left( {1;0;0} \right);D'\left( {0;1;0} \right);A\left( {0;0;1} \right)$.
Xác định tọa độ các điểm M, N.
Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau \(d\left( {MN;B'D'} \right) = \dfrac{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right].\overrightarrow {NB'} } \right|}}{{\left| {\left[ {\overrightarrow {B'D'} ;\overrightarrow {MN} } \right]} \right|}}\)
Cách 2: Xác định mặt phẳng (P) chứa B’D’ và song song với MN, khi đó
\(d\left( {MN;B'D'} \right) = d\left( {B'D';\left( P \right)} \right) = d\left( {O;\left( P \right)} \right)\) (với O là trung điểm của \(B'D'\)).