Cho hàm số \(y=\dfrac{x-2}{x+1}\) có đồ thị (C). Tiếp tuyến d của đồ thị (C) tạo với hai tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó khoảng cách từ \(I(-1;1)\) đến \(d\) bằng
Phương trình tiếp tuyến tại điểm x = a là :
\(y=\dfrac{3}{{{\left( a+1 \right)}^{2}}}\left( x-a \right)+\dfrac{a-2}{a+1}\) ( d )
Đường thẳng d cắt các tiệm cận tại : \(A\left( -1;\dfrac{{{a}^{2}}-4a-5}{{{\left( a+1 \right)}^{2}}} \right);B\left( 2a+1;1 \right)\)
Suy ra:
\(\begin{align} & AI=\left| \dfrac{6}{a+1} \right|;BI=|2a+2| \\ & =>AI.BI=12,\forall a \\\end{align}\)
Áp dụng công thức ở phần phương pháp ta có :
\(r=\dfrac{AI.BI}{AI+BI+\sqrt{A{{I}^{2}}+B{{I}^{2}}}}\le \dfrac{12}{2\sqrt{AI.BI}+\sqrt{2AI.BI}}=\dfrac{\sqrt{6}}{1+\sqrt{2}}\)
Dấu bằng xảy ra khi AI=BI , suy ra tam giác ABI vuông cân , suy ra khoảng cách từ I tới d bằng \(\sqrt{6}\)
Cho hàm số \(y=\dfrac{4x-3}{x-3}\) có đồ thị \(C\). Biết đồ thị \(\left( C \right)\) có hai điểm phân biệt M, N và khoảng cách từ M hoặc N đến hai đường tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng:
TXĐ: \(D=R\backslash \left\{ 3 \right\}\)
Đồ thị hàm số có đường TCN \(y=4\,\,\left( {{d}_{1}} \right)\) và TCĐ \(x=3\,\,\left( {{d}_{2}} \right)\).
Gọi điểm \(M\in \left( C \right)\) có dạng \(M\left( a;\dfrac{4a-3}{a-3} \right)\) khi đó ta có:
\(\begin{align}d\left( M;{{d}_{2}} \right)=\left| a-3 \right|;\,\,d\left( M;{{d}_{1}} \right)=\left| \dfrac{4a-3}{a-3}-4 \right|=\dfrac{9}{\left| a-3 \right|} \\\Rightarrow d\left( M;{{d}_{2}} \right)+d\left( M;{{d}_{1}} \right)=\left| a-3 \right|+\dfrac{9}{\left| a-3 \right|}\ge 2\sqrt{9}=3 \\\end{align}\)
Dấu = xảy ra \(\Leftrightarrow \left| a-3 \right|=\dfrac{9}{\left| a-3 \right|}\Leftrightarrow {{\left( a-3 \right)}^{2}}=9\Leftrightarrow \left[ \begin{align}a=6 \\a=0 \\\end{align} \right.\)
\(\Rightarrow M\left( 6;7 \right),\,\,N\left( 0;1 \right)\Rightarrow MN=\sqrt{{{6}^{2}}+{{6}^{2}}}=6\sqrt{2}\)
Cho hàm số \(y = \dfrac{{ax + b}}{{x + 1}}\) có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:
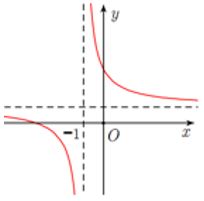
Đồ thị hàm số có đường tiệm cận ngang \(y = a\). Theo hình vẽ, ta có: \(a > 0.\)
Đồ thị hàm số cắt trục hoành tại điểm \(A\left( { - \dfrac{b}{a};0} \right)\)
Theo hình vẽ, ta có: \( - \dfrac{b}{a} < - 1 \Leftrightarrow \dfrac{b}{a} > 1 \Rightarrow \dfrac{{b - a}}{a} > 0\).
Mà \(a > 0 \Rightarrow b - a > 0 \Leftrightarrow b > a\)
Vậy \(b > a > 0\).
Gọi \(M\left( a;b \right)\) là điểm trên đồ thị hàm số \(y=\dfrac{2x+1}{x+2}\) mà có khoảng cách đến đường thẳng \(d:y=3x+6\) nhỏ nhất. Khi đó
Điểm \(M\left( a;b \right)\in \left( H \right)\Rightarrow M\left( a;\dfrac{2a+1}{a+2} \right)\)
\(\Rightarrow \)\(d\left( M;\left( d \right) \right)=\dfrac{\left| 3a-\dfrac{2a+1}{a+2}+6 \right|}{\sqrt{10}}\) \(=\dfrac{1}{\sqrt{10}}.\left| \dfrac{3{{a}^{2}}+10a+11}{a+2} \right|.\)
Xét hàm số \(f\left( a \right)=\dfrac{3{{a}^{2}}+10a+11}{a+2}\) với \(a\ne -\,2,\) có \({f}'\left( a \right)=\dfrac{3\left( {{a}^{2}}+4a+3 \right)}{{{\left( a+2 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{align} & a=-\,1 \\ & a=-\,3 \\\end{align} \right..\)
Tính các giá trị \(f\left( -1 \right)=4;\,\,f\left( -\,3 \right)=-\,8\) và \(\mathop {\lim }\limits_{x{\kern 1pt} \to - 2} f\left( a \right) = \infty ;\mathop {\lim }\limits_{x \to \infty } f\left( a \right) = \infty \)
Suy ra giá trị nhỏ nhất của hàm số \(\left| f\left( a \right) \right|\) bằng \(4\,\,\Leftrightarrow \,\,a=-\,1.\)
Vậy \(\left\{ \begin{align} & a=-\,1 \\ & b=-\,1 \\\end{align} \right.\Rightarrow a+b=-\,2.\)
Cho hàm số \(y=\dfrac{x+1}{-1+x}\) có đồ thị (C). Tiếp tuyến tại điểm M bất kì thuộc (C) cắt 2 đường tiệm cận của (C) tạo thành một tam giác. Tính diện tích của tam giác đó.
Đồ thị hàm số có đường tiệm cận ngang \(y=1\,\,\left( {{d}_{1}} \right)\) và tiệm cận đứng \(x=1\,\,\left( {{d}_{2}} \right)\).
Gọi \(A={{d}_{1}}\cap {{d}_{2}}\Rightarrow A\left( 1;1 \right)\)
\(y'=\dfrac{1.\left( -1 \right)-1.1}{{{\left( -1+x \right)}^{2}}}=-\dfrac{2}{{{\left( x-1 \right)}^{2}}}\)
Gọi \(M\left( {{x}_{0}};\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1} \right)\in \left( C \right)\) ta có tiếp tuyến tại M của đồ thị hàm số là \(y=-\dfrac{2}{{{\left( {{x}_{0}}-1 \right)}^{2}}}\left( x-{{x}_{0}} \right)+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}\,\,\,\left( d \right)\)
Cho \(x = 1\) \(\Rightarrow y=-\dfrac{2}{{{\left( {{x}_{0}}-1 \right)}^{2}}}\left( 1-{{x}_{0}} \right)+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}\) \(=\dfrac{2}{{{x}_{0}}-1}+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}=\dfrac{{{x}_{0}}+3}{{{x}_{0}}-1}\)
Gọi \(B=d\cap {{d}_{2}}\Rightarrow B\left( 1;\dfrac{{{x}_{0}}+3}{{{x}_{0}}-1} \right)\)
Cho \(y = 1\)
\(\begin{array}{l}\Rightarrow 1 = - \dfrac{2}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{{x_0} + 1}}{{{x_0} - 1}}\\ \Leftrightarrow 1 = - \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{2{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{{x_0} + 1}}{{{x_0} - 1}}\\ \Leftrightarrow \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{2{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{{x_0} + 1}}{{{x_0} - 1}} - 1\\ \Leftrightarrow \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{2{x_0} + x_0^2 - 1 - x_0^2 + 2{x_0} - 1}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{4{x_0} - 2}}{{{{\left( {{x_0} - 1} \right)}^2}}}\\ \Leftrightarrow x = 2{x_0} - 1\end{array}\)
Gọi \(C=d\cap {{d}_{1}}\Rightarrow C\left( 2{{x}_{0}}-1;1 \right)\)
Tam giác ABC là tam giác vuông tại A có
\(\begin{array}{l}AB = \sqrt {{{\left( {\dfrac{{{x_0} + 3}}{{{x_0} - 1}} - 1} \right)}^2}} = \dfrac{4}{{\left| {{x_0} - 1} \right|}},\,\,AC = \sqrt {{{\left( {2{x_0} - 1 - 1} \right)}^2}} = \left| {2{x_0} - 2} \right| = 2\left| {{x_0} - 1} \right|\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}\dfrac{4}{{\left| {{x_0} - 1} \right|}}.2\left| {{x_0} - 1} \right| = 4\end{array}\)
Cho hàm số \(y=\dfrac{1-3x}{3-x}\) có đồ thị \(\left( C \right)\) Điểm M nằm trên \(\left( C \right)\) sao cho khoảng cách từ M đến tiệm cận đứng gấp hai lần khoảng cách từ M đến tiệm cận ngang của \(\left( C \right)\). Khoảng cách từ M đến tâm đối xứng của \(\left( C \right)\) bằng:
Đồ thị hàm số \(\left( C \right)\) có TCĐ \(x=3\,\,\left( {{d}_{1}} \right)\) và TCN: \(y=3\,\,\left( {{d}_{2}} \right)\)
\(\Rightarrow \) Tâm đối xứng của đồ thị \(\left( C \right)\) là: \(I\left( 3;3 \right)\)
Gọi \(M\left( m;\dfrac{1-3m}{3-m} \right)\in \left( C \right)\) ta có: \(d\left( M;{{d}_{1}} \right)=\left| m-3 \right|;\) \(d\left( M;\left( {{d}_{2}} \right) \right)=\left| \dfrac{1-3m}{3-m}-3 \right|=\dfrac{8}{\left| 3-m \right|}\)
Vì \(d\left( {M;\left( {{d_1}} \right)} \right) = 2d\left( {M;\left( {{d_2}} \right)} \right)\) \( \Rightarrow \left| {m - 3} \right| = \dfrac{{16}}{{\left| {3 - m} \right|}}\) \(\Leftrightarrow {\left( {m - 3} \right)^2} = 16 \Leftrightarrow \left[ \begin{array}{l}
m = 7\\
m = - 1
\end{array} \right.\)
Khi \(m=7\Rightarrow M\left( 7;5 \right)\) \(\Rightarrow IM=\sqrt{{{\left( 7-3 \right)}^{2}}+{{\left( 5-3 \right)}^{2}}}=2\sqrt{5}\)
Khi \(m=-1\Rightarrow M\left( -1;1 \right)\) \(\Rightarrow IM=\sqrt{{{\left( -1-3 \right)}^{2}}+{{\left( 1-3 \right)}^{2}}}=2\sqrt{5}\)
Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) bằng
Đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) có tâm đối xứng là \(I\left( -\,1;2 \right)\) \(\Rightarrow OI=\sqrt{{{\left( -\,1 \right)}^{2}}+{{2}^{2}}}=\sqrt{5}.\)
Cho hàm số \(y=\dfrac{2x+1}{x-2}\). Khẳng định nào dưới đây là đúng?
Xét hàm số \(y=\dfrac{2x+1}{x-2}\):
+) \(\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{2x + 1}}{{x - 2}} = + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{2x + 1}}{{x - 2}} = - \infty \)
Đồ thị hàm số có tiệm cận đứng là \(x=2\). Phương án A: đúng.
+) \(y'=-\dfrac{5}{{{(x-2)}^{2}}}<0,\,\,\forall x\ne 2\) \(\Rightarrow \) Hàm số \(y=\dfrac{2x+1}{x-2}\) không có cực trị và hàm số nghịch biến trên các khoảng \(\left( -\infty ;2 \right);\,\,\left( 2;+\infty \right)\). Phương án B và D: sai.
+) Ta có: \(3=\dfrac{2.1+1}{1-2}\) vô lí \(\Rightarrow \) Đồ thị hàm số không đi qua điểm\(A(1;3)\). Phương án C: sai.
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ.
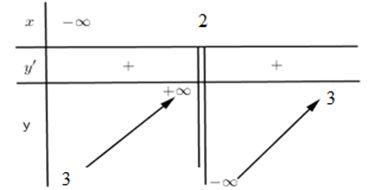
Khẳng định nào sau đây sai?
Đáp án A: Đồ thị hàm số \(y=f\left( x \right)\) cắt đường thẳng \(y=5\) tại 1 điểm duy nhất có hoành độ \(x<2\) nên A sai.
Đáp án B: \(x=2\) là tiệm cận đứng của đồ thị hàm số vì \(\mathop {\lim }\limits_{x \to {2^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = - \infty \) nên B đúng.
Đáp án C: Hàm số đồng biến trên khoảng \(\left( -\infty ;2 \right)\) nên cũng đồng biến trên \(\left( -\infty ;1 \right)\subset \left( -\infty ;2 \right)\) nên C đúng.
Đáp án D: Hàm số đồng biến trên trên \(\left( 2;+\infty \right)\) nên đồng biến trên \(\left[ 3;10 \right]\), do đó \(\mathop {\max }\limits_{x \in \left[ {3;10} \right]} f\left( x \right) = f\left( {10} \right)\) nên D đúng.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
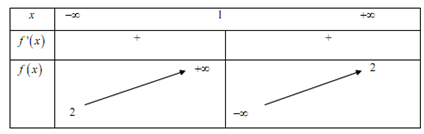
A sai vì đồ thị hàm số có đường tiệm cận đứng là \(x = 1\)
C sai vì đồ thị hàm số có đường tiệm cận ngang chứ không phải là hàm số có tiệm cận ngang
D sai vì hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
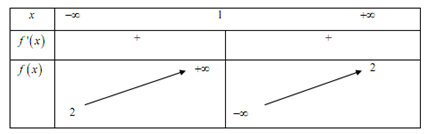
A sai vì đồ thị hàm số có đường tiệm cận đứng là \(x = 1\)
C sai vì đồ thị hàm số có đường tiệm cận ngang chứ không phải là hàm số có tiệm cận ngang
D sai vì hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
Cho hàm số \(y = \dfrac{{ax - 1}}{{x + d}}\) có bảng biến thiên
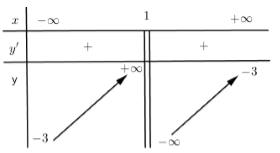
Giá trị của \({a^2} - {d^2}\) bằng
Xét hàm số \(y = \dfrac{{ax - 1}}{{x + d}}\)
+) Tiệm cận đứng \(x = - d\) mà theo bảng biến thiên tiệm cận đứng của đồ thị hàm số là \(x = 1\) suy ra \(d = - 1\)
+) Tiệm cận ngang \(y = \dfrac{a}{1}\) mà theo bảng biến thiên tiệm cận ngang của đồ thị hàm số là \(y = - 3\) suy ra \(a = - 3\)
Vậy: \({a^2} - {d^2} = {\left( { - 3} \right)^2} - {\left( { - 1} \right)^2} = 8\)
Cho hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có bảng biến thiên:
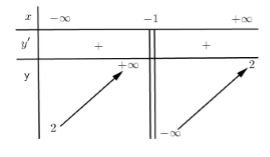
Giá trị của \(2{c^2} - 5{d^2}\) bằng
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có\( \Rightarrow \left\{ \begin{array}{l}c = 1\\d = 1\end{array} \right.\) \( \Rightarrow 2{c^2} - 5{d^2} = {2.1^2} - {5.1^2} = - 3\)
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{2x + d}}\) như hình vẽ bên.
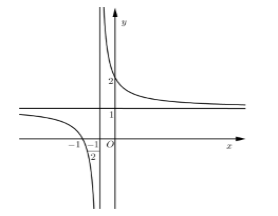
Chọn khẳng định đúng
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{2x + d}}\) có \( \Rightarrow 2a - d = 3\)
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên
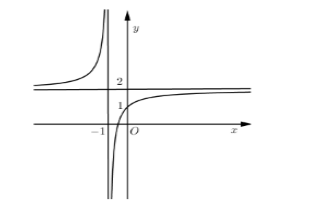
Chọn khẳng định đúng
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có
Hàm số có dạng \(y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)\)
Ta có điểm \(\left( {0;1} \right) \in \left( C \right)\)
Thay \(x = 0\) và \(y = 1\) vào hàm số ta được \(1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1\) \( \Rightarrow 2b = c + d\)
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{cx + b}}\) như hình vẽ bên.
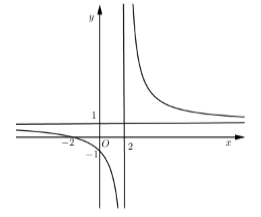
Chọn khẳng định đúng
Ta có đồ thị hàm số\(y = \dfrac{{ax + 2}}{{cx + b}}\) đi qua điểm có tọa độ \(\left( {0; - 1} \right)\).
Thay \(x = 0;\,y = - 1\) vào hàm số ta được \( - 1 = \dfrac{{a.0 + 2}}{{c.0 + b}} \Rightarrow b = - 2\)
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{cx - 2}}\) có \( \Rightarrow a = 1;\,b = - 2;\,c = 1\)
Hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ với $a > 0$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
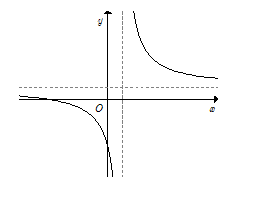
Từ đồ thị hàm số, ta thấy
Khi $y = 0 \Rightarrow x = - \dfrac{b}{a} < 0 \Rightarrow b > 0.$
Khi $x = 0 \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow d < 0$.
Đồ thị hàm số có tiệm cận đứng $x = - \dfrac{d}{c} > 0 \Rightarrow c > 0.$
Vậy $b > 0,{\rm{ }}c > 0,{\rm{ }}d < 0.$
Hàm số $y = \dfrac{{bx - c}}{{x - a}}$ $\left( {a \ne 0;} \right.$ $\left. {a,{\rm{ }}b,{\rm{ }}c \in \mathbb{R}} \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
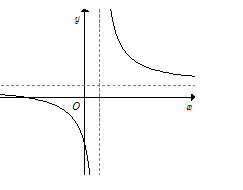
Đồ thị hàm số có tiệm cận đứng $x = a > 0$; tiệm cận ngang \(y = b > 0.\)
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
Vậy \(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab < 0.\)
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) như hình vẽ bên
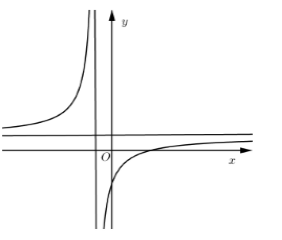
Chọn khẳng định đúng
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có:
- TCĐ: \(x = - \dfrac{d}{c} < 0 \Rightarrow cd > 0\) loại D.
- TCN: \(y = \dfrac{a}{c} > 0 \Rightarrow ac > 0\) suy ra \(ad > 0\). B đúng.
- Giao \(Ox:y = 0 \Rightarrow x = - \dfrac{b}{a} > 0 \Rightarrow ab < 0\)\( \Rightarrow bc < 0\). Loại A.
- Giao \(Oy:x = 0 \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0 \Rightarrow \)Loại C.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
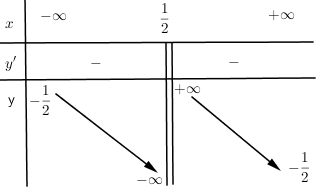
Khẳng định nào sau đây là đúng?
$x = \dfrac{1}{2}$ là tiệm cận đứng của đồ thị hàm số
$y = - \dfrac{1}{2}$ là tiệm cận ngang của đồ thị hàm số
Hàm số nghịch biến trên $\left( { - \infty ;\,\dfrac{1}{2}} \right)$ và $\left( {\dfrac{1}{2};\, + \infty } \right)$

