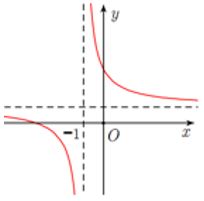
Cho hàm số \(y=\dfrac{x+1}{-1+x}\) có đồ thị (C). Tiếp tuyến tại điểm M bất kì thuộc (C) cắt 2 đường tiệm cận của (C) tạo thành một tam giác. Tính diện tích của tam giác đó.

Đồ thị hàm số có đường tiệm cận ngang \(y=1\,\,\left( {{d}_{1}} \right)\) và tiệm cận đứng \(x=1\,\,\left( {{d}_{2}} \right)\).

Gọi \(A={{d}_{1}}\cap {{d}_{2}}\Rightarrow A\left( 1;1 \right)\)

\(y'=\dfrac{1.\left( -1 \right)-1.1}{{{\left( -1+x \right)}^{2}}}=-\dfrac{2}{{{\left( x-1 \right)}^{2}}}\)

Gọi \(M\left( {{x}_{0}};\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1} \right)\in \left( C \right)\) ta có tiếp tuyến tại M của đồ thị hàm số là \(y=-\dfrac{2}{{{\left( {{x}_{0}}-1 \right)}^{2}}}\left( x-{{x}_{0}} \right)+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}\,\,\,\left( d \right)\)

Cho \(x  = 1\) \(\Rightarrow y=-\dfrac{2}{{{\left( {{x}_{0}}-1 \right)}^{2}}}\left( 1-{{x}_{0}} \right)+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}\) \(=\dfrac{2}{{{x}_{0}}-1}+\dfrac{{{x}_{0}}+1}{{{x}_{0}}-1}=\dfrac{{{x}_{0}}+3}{{{x}_{0}}-1}\)

Gọi \(B=d\cap {{d}_{2}}\Rightarrow B\left( 1;\dfrac{{{x}_{0}}+3}{{{x}_{0}}-1} \right)\)

Cho \(y = 1\)

\(\begin{array}{l}\Rightarrow 1 =  - \dfrac{2}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{{x_0} + 1}}{{{x_0} - 1}}\\ \Leftrightarrow 1 =  - \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{2{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{{x_0} + 1}}{{{x_0} - 1}}\\ \Leftrightarrow \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{2{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{{x_0} + 1}}{{{x_0} - 1}} - 1\\ \Leftrightarrow \dfrac{{2x}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{2{x_0} + x_0^2 - 1 - x_0^2 + 2{x_0} - 1}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{4{x_0} - 2}}{{{{\left( {{x_0} - 1} \right)}^2}}}\\ \Leftrightarrow x = 2{x_0} - 1\end{array}\)

 Gọi \(C=d\cap {{d}_{1}}\Rightarrow C\left( 2{{x}_{0}}-1;1 \right)\)

 Tam giác ABC là tam giác vuông tại A có

\(\begin{array}{l}AB = \sqrt {{{\left( {\dfrac{{{x_0} + 3}}{{{x_0} - 1}} - 1} \right)}^2}}  = \dfrac{4}{{\left| {{x_0} - 1} \right|}},\,\,AC = \sqrt {{{\left( {2{x_0} - 1 - 1} \right)}^2}}  = \left| {2{x_0} - 2} \right| = 2\left| {{x_0} - 1} \right|\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}\dfrac{4}{{\left| {{x_0} - 1} \right|}}.2\left| {{x_0} - 1} \right| = 4\end{array}\)