Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ.
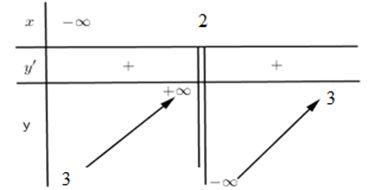
Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án A: Đồ thị hàm số \(y=f\left( x \right)\) cắt đường thẳng \(y=5\) tại 1 điểm duy nhất có hoành độ \(x<2\) nên A sai.
Đáp án B: \(x=2\) là tiệm cận đứng của đồ thị hàm số vì \(\mathop {\lim }\limits_{x \to {2^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = - \infty \) nên B đúng.
Đáp án C: Hàm số đồng biến trên khoảng \(\left( -\infty ;2 \right)\) nên cũng đồng biến trên \(\left( -\infty ;1 \right)\subset \left( -\infty ;2 \right)\) nên C đúng.
Đáp án D: Hàm số đồng biến trên trên \(\left( 2;+\infty \right)\) nên đồng biến trên \(\left[ 3;10 \right]\), do đó \(\mathop {\max }\limits_{x \in \left[ {3;10} \right]} f\left( x \right) = f\left( {10} \right)\) nên D đúng.
Hướng dẫn giải:
Xét tính đúng sai của các đáp án dựa vào sự tương giao giữa hai đồ thị, sự đồng biến, nghịch biến của hàm số, tiệm cận đứng, tiệm cận ngang của đồ thị hàm số,…