Gọi \(d\) là đường thẳng đi qua $A\left( {2;0} \right)$ có hệ số góc \(m\) cắt đồ thị $\left( C \right):y = - {x^3} + 6{x^2} - 9x + 2$ tại ba điểm phân biệt \(A\), \(B\), \(C\). Gọi \(B'\), \(C'\) lần lượt là hình chiếu vuông góc của \(B\), \(C\) lên trục tung. Tìm giá trị dương của \(m\) để hình thang \(BB'C'C\) có diện tích bằng $8.$
Phương trình đường thẳng $d:y = m\left( {x - 2} \right)$
Phương trình hoành độ giao điểm của \(d\) và \(\left( C \right)\) là:
$ - {x^3} + 6{x^2} - 9x + 2 = m\left( {x - 2} \right)$$ \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} - 4x + m + 1} \right) = 0$$ \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow A\left( {2;0} \right)\\{x^2} - 4x + m + 1 = 0\,\,\left( 1 \right)\end{array} \right.$
Để đồ thị hàm số $\left( C \right)$ cắt \(d\) tại 3 điểm phân biệt thì phương trình \(\left( 1 \right)\) phải có hai nghiệm phân biệt \(x \ne 2\)
ĐK: $\left\{ \begin{array}{l}\Delta > 0\\4 - 8 + m + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 - m - 1 > 0\\m - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 3\\m \ne 3\end{array} \right. \Leftrightarrow m < 3$
Giả sử $B\left( {{x_1};m{x_1} - 2m} \right),$$C\left( {{x_2};m{x_2} - 2m} \right)$ với \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình \(\left( 1 \right)\)
Theo Viet $\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m + 1\end{array} \right.$.
Vì \(m > 0 \Rightarrow {x_1} > 0\) và \({x_2} > 0\). Ta có $B'\left( {0,m{x_1} - 2m} \right),$$C'\left( {0,m{x_2} - 2m} \right)$
Ta có ${S_{BB'C'C}} = \dfrac{1}{2}B'C'\left( {BB' + CC'} \right) = 8 \Leftrightarrow B'C'\left( {BB' + CC'} \right) = 16\,\,\left( * \right)$
Mà $B'C' = \left| {m\left( {{x_1} - {x_2}} \right)} \right|$, $BB' = \left| {{x_1}} \right| = {x_1}$ và $CC' = \left| {{x_2}} \right| = {x_2}$
Do đó \(\left( * \right) \Leftrightarrow m\left| {{x_1} - {x_2}} \right|\left( {{x_1} + {x_2}} \right) = 16 \Leftrightarrow m\left| {{x_1} - {x_2}} \right| = 4 \Leftrightarrow {m^2}{\left( {{x_1} - {x_2}} \right)^2} = 16\)
$ \Leftrightarrow {m^2}\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right] = 16$$ \Leftrightarrow {m^2}\left( {16 - 4m - 4} \right) = 16$$ \Leftrightarrow {m^3} - 3{m^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.$
Kết hợp với \(m > 0\) và \(m < 3\) ta có \(m = 2\)
Tìm tất cả các giá trị thực của tham số \(m\) sao cho đồ thị hàm số \(y = \dfrac{{x + 1}}{{\sqrt[{}]{{{m^2}{x^2} + m - 1}}}}\) có bốn đường tiệm cận.
Với \(m = 0\) thì hàm số không xác định. Do đó \(m \ne 0\) \(\left( 1 \right)\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + 1}}{{\sqrt[{}]{{{m^2}{x^2} + m - 1}}}} = \dfrac{1}{{\left| m \right|}}\) và \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + 1}}{{\sqrt[{}]{{{m^2}{x^2} + m - 1}}}} = \dfrac{{ - 1}}{{\left| m \right|}}\).
\( \Rightarrow \)đồ thị hàm số có 2 đường tiệm cận ngang.
Để đồ thị hàm số có bốn đường tiệm cận thì cần tìm \(m\) để đồ thị hàm số có 2 đường tiệm cận đứng, nghĩa là cần tìm \(m\) để phương trình \(g\left( x \right) = {m^2}{x^2} + m - 1 = 0\) có hai nghiệm phân biệt khác \( - 1\)
ĐK: \(\left\{ \begin{array}{l}\Delta = - 4{m^2}\left( {m - 1} \right) > 0\\g\left( { - 1} \right) = {m^2} + m - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m \ne 0\\m \ne \dfrac{{ - 1 \pm \sqrt 5 }}{2}\end{array} \right.\,\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m \ne 0\\m \ne \dfrac{{ - 1 \pm \sqrt 5 }}{2}\end{array} \right.\,\) \(\left( 2 \right)\)
Kết hợp \(\left( 1 \right)\)\(\left( 2 \right)\)có \(\left\{ \begin{array}{l}m < 1\\m \ne 0\\m \ne \dfrac{{ - 1 \pm \sqrt 5 }}{2}\end{array} \right.\,\)
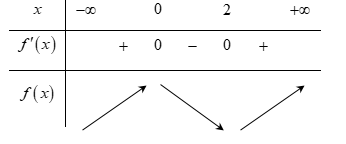
Cho hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình bên. Đặt $g\left( x \right) = f\left( {\sqrt {{x^2} + x + 2} } \right)$. Chọn khẳng định đúng trong các khẳng định sau
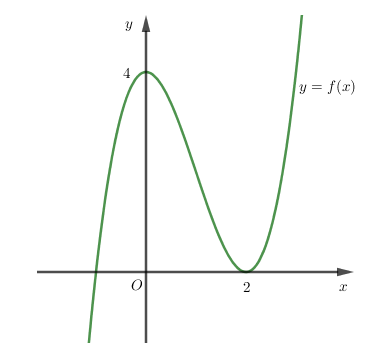
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ ; $f'\left( x \right) = 3a{x^2} + 2bx + c$, có đồ thị như hình vẽ.
Do đó $x = 0 \Rightarrow d = 4$; $x = 2 \Rightarrow 8a + 4b + 2c + d = 0$; $f'\left( 2 \right) = 0 \Rightarrow 12a + 4b + c = 0$; $f'\left( 0 \right) = 0 \Rightarrow c = 0$.
Tìm được $a = 1;b = - 3;c = 0;d = 4$ và hàm số $y = {x^3} - 3{x^2} + 4$
Ta có $g\left( x \right) = f\left( {\sqrt {{x^2} + x + 2} } \right)$$ = {\left( {\sqrt {{x^2} + x + 2} } \right)^3} - 3\left( {{x^2} + x + 2} \right) + 4$ $ \Rightarrow g'\left( x \right) = \dfrac{3}{2}\left( {2x + 1} \right)\sqrt {{x^2} + x + 2} - 3\left( {2x + 1} \right) = 3\left( {2x + 1} \right)\left( {\dfrac{1}{2}\sqrt {{x^2} + x + 2} - 1} \right)$
$g'\left( x \right) = 0 \Rightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\\x = - 2\end{array} \right.$
Bàng xét dấu của $g\left( x \right)$:
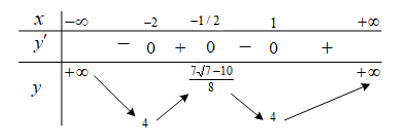
Vậy $g\left( x \right)$ nghịch biến trên khoảng $\left( {\dfrac{{ - 1}}{2};0} \right)$.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên \(\mathbb{R}\), phương trình \(f'\left( x \right) = 0\) có \(4\) nghiệm thực và đồ thị hàm số \(f'\left( x \right)\) như hình vẽ. Tìm số điểm cực trị của hàm số \(y = f\left( {{x^2}} \right)\).
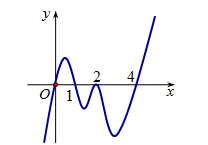
Ta có: \(y' = 2x.f'\left( {{x^2}} \right)\)
\(y' = 0\) \( \Leftrightarrow \left[ \begin{array}{l}2x = 0\\{x^2} = 0\\{x^2} = 1\\{x^2} = 2\\{x^2} = 4\end{array} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 0}\\{x = \pm 1}\\{x = \pm \sqrt 2 }\\{x = \pm 2}\end{array}} \right.\)
\(f'\left( {{x^2}} \right) > 0\)\( \Leftrightarrow \left[ \begin{array}{l}{x^2} > 4\\0 < {x^2} < 1\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < - 2\\ - 1 < x < 1\end{array} \right.\)
Bảng xét dấu:
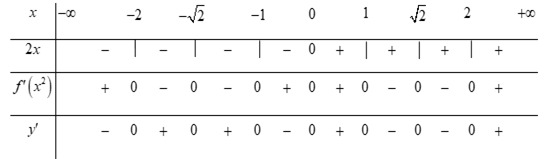
Quan sát bảng xét dấu ta thấy: Qua $5$ điểm $x=2,x=-1,x=0,x=1,x=2$ là $y'$ đổi dấu.
Vậy hàm số có $5$ điểm cực trị.
Cho đường cong \(\left( C \right):y = \dfrac{{2x + 3}}{{x - 1}}\) và \(M\) là một điểm nằm trên \(\left( C \right)\). Giả sử \({d_1}\), \({d_2}\) tương ứng là các khoảng cách từ \(M\) đến hai tiệm cận của \(\left( C \right)\), khi đó \({d_1}.{d_2}\) bằng:
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \)\( \Rightarrow x = 1\) là tiệm cận đứng; \(\mathop {\lim }\limits_{x \to + \infty } y = 2\)\( \Rightarrow y = 2\) là tiệm cận ngang.
\(M \in \left( C \right)\)\( \Rightarrow M\left( {a;\,2 + \dfrac{5}{{a - 1}}} \right)\) với \(a \ne 1\).
Khoảng cách từ \(M\) đến tiệm cận đứng: \({d_1} = \dfrac{{\left| {a - 1} \right|}}{{\sqrt 1 }} = \left| {a - 1} \right|\),
Khoảng cách từ \(M\) đến tiệm ngang \({d_2} = \dfrac{{\left| {2 + \dfrac{5}{{a - 1}} - 2} \right|}}{{\sqrt {{0^2} + {1^2}} }} = \left| {\dfrac{5}{{a - 1}}} \right|\).
Ta có: \({d_1}.{d_2} = \left| {a - 1} \right|.\left| {\dfrac{5}{{a - 1}}} \right| = \left| {\left( {a - 1} \right).\dfrac{5}{{a - 1}}} \right| = 5\).
Hai điểm \(M\) ; \(N\) lần lượt thuộc hai nhánh của đồ thị hàm số \(y = \dfrac{{3x - 1}}{{x - 3}}\). Khi đó độ dài đoạn thẳng \(MN\) ngắn nhất bằng:
Ta có \(y = \dfrac{{3x - 1}}{{x - 3}}\)\( \Rightarrow y = 3 + \dfrac{8}{{x - 3}}\)\( \Rightarrow y - 3 = \dfrac{8}{{x - 3}}\)
Đặt \(\left\{ \begin{array}{l}X = x - 3\\Y = y - 3\end{array} \right.\). Ta có \(Y = \dfrac{8}{X}\).
Gọi $M\left( {{X_1};\,\,\dfrac{8}{{{X_1}}}} \right)$ thuộc nhánh trái, $N\left( {{X_2};\,\dfrac{8}{{{X_2}}}} \right)$ thuộc nhánh phải của đồ thị hàm số,
Với ${X_1} < 0 < {X_2}$. Ta có: $M{N^2} = {\left( {{X_2} - {X_1}} \right)^2} + 64{\left( {\dfrac{1}{{{X_2}}} - \dfrac{1}{{{X_1}}}} \right)^2}$
$ \Rightarrow M{N^2} \ge 2\sqrt {{{\left( {{X_2} - {X_1}} \right)}^2}.64{{\left( {\dfrac{1}{{{X_2}}} - \dfrac{1}{{{X_1}}}} \right)}^2}} $$ \Rightarrow M{N^2} \ge 16\left| {\left( {{X_2} - {X_1}} \right)\left( {\dfrac{1}{{{X_2}}} - \dfrac{1}{{{X_1}}}} \right)} \right|$
$ \Rightarrow M{N^2} \ge 16\dfrac{{{{\left( {{X_2} - {X_1}} \right)}^2}}}{{\left| {{X_1}{X_2}} \right|}}$$ \Rightarrow M{N^2} \ge 16\dfrac{{ - 4{X_1}{X_2}}}{{ - {X_1}{X_2}}} = 64$.
Do vậy $MN \ge 8$.
Dấu bằng xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}{X_2} = - {X_1}\\{\left( {{X_2} - {X_1}} \right)^2} = 64{\left( {\dfrac{1}{{{X_2}}} - \dfrac{1}{{{X_1}}}} \right)^2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{X_1} = - 2\sqrt 2 \\{X_2} = 2\sqrt 2 \end{array} \right.$
Vậy với $M = \left( { - 2\sqrt 2 ;\,\, - 2\sqrt 2 } \right)$ ; $N = \left( {2\sqrt 2 ;\,\,2\sqrt 2 } \right)$ thì \(MN\) có độ dài ngắn nhất bằng \(8\).
Cách khác: Do $M,N$ thuộc hai nhánh khác nhau nên ta có \(M\left( {3 - \alpha ;3 - \dfrac{8}{\alpha }} \right);N\left( {3 + \beta ;3 + \dfrac{8}{\beta }} \right)\), với \(\alpha ;\beta > 0\).
Khi đó \(M{N^2} = {\left( {\alpha + \beta } \right)^2} + {\left( {\dfrac{8}{\alpha } + \dfrac{8}{\beta }} \right)^2}\)\( = {\left( {\alpha + \beta } \right)^2} + \dfrac{{64{{\left( {\alpha + \beta } \right)}^2}}}{{{{\left( {\alpha \beta } \right)}^2}}}\)
\( = {\left( {\alpha + \beta } \right)^2}\left( {1 + \dfrac{{64}}{{{{\left( {\alpha \beta } \right)}^2}}}} \right) \ge 4\alpha \beta \left( {1 + \dfrac{{64}}{{{{\left( {\alpha \beta } \right)}^2}}}} \right)\) \( = 4\left( {\alpha \beta + \dfrac{{64}}{{\alpha \beta }}} \right) \ge 4.2.8 = 64\).
Vậy \(M{N_{\min }} = 8\) khi \(\left\{ \begin{array}{l}\alpha = \beta \\\alpha \beta = \dfrac{{64}}{{\alpha \beta }}\end{array} \right. \Leftrightarrow \alpha = \beta = 2\sqrt 2 \)
Cho hàm số $y = \dfrac{{a{x^2} + x - 1}}{{4{x^2} + bx + 9}}$ có đồ thị $\left( C \right)$, trong đó $a$, $b$ là các hằng số dương thỏa mãn $a.b = 4$. Biết rằng $\left( C \right)$ có đường tiệm cận ngang $y = c$ và có đúng $1$ đường tiệm cận đứng. Tính tổng $T = 3a + b - 24c$.
Theo giả thiết \(a > 0\), \(b > 0\).
Với \(ab = 4\) ta có $y = \dfrac{{a{x^2} + x - 1}}{{4{x^2} + bx + 9}} = \dfrac{{\dfrac{4}{b}{x^2} + x - 1}}{{4{x^2} + bx + 9}} = \dfrac{{4{x^2} + bx - b}}{{b\left( {4{x^2} + bx + 9} \right)}} = \dfrac{1}{b} - \dfrac{{b + 9}}{{b\left( {4{x^2} + bx + 9} \right)}}$
Đồ thị $\left( C \right)$ có đúng $1$ đường tiệm cận đứng nên $4{x^2} + bx + 9 = 0$ có nghiệm kép
Suy ra $\Delta = {b^2} - 4.4.9 = 0 \Leftrightarrow b = 12$ (do \(b > 0\))
Ta có \(ab = 4\) suy ra \(a = \dfrac{1}{3}\); $c = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{a{x^2} + x - 1}}{{4{x^2} + bx + 9}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{a + \dfrac{1}{x} - \dfrac{1}{{{x^2}}}}}{{4 + \dfrac{b}{x} + \dfrac{9}{{{x^2}}}}} = \dfrac{a}{4}$ suy ra \(c = \dfrac{1}{{12}}\)
Vậy $T = 3a + b - 24c = 11$
Cho hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị của hàm $y = f'\left( x \right)$ như hình vẽ. Biết rằng $f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)$. Giá trị nhỏ nhất và giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ {0;5} \right]$ lần lượt là:
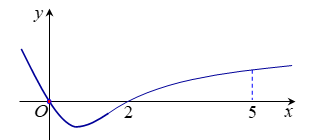
Dựa vào đồ thị của hàm số $y = f'\left( x \right)$ ta có bảng biến thiên của hàm số $y = f\left( x \right)$:
Quan sát bảng biến thiên ta thấy:
$f\left( 2 \right) < f\left( 3 \right) < f\left( 5 \right)$ và $f\left( 0 \right) > f\left( 2 \right)$
Mặt khác $f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow $$f\left( 3 \right) - f\left( 2 \right) = f\left( 5 \right) - f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)$
Vậy trên đoạn $\left[ {0;5} \right]$ hàm số $y = f\left( x \right)$ có: $f\left( 2 \right) < f\left( 0 \right) < f\left( 5 \right)$
Do đó:
+) \(GTNN\) của hàm số trên đoạn \(\left[ {0;5} \right]\) là \(f\left( 2 \right)\)
+) \(GTLN\) của hàm số trên đoạn \(\left[ {0;5} \right]\) là \(f\left( 5 \right)\)
Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị $f'\left( x \right)$ như hình vẽ. Đặt $g\left( x \right) = f\left( x \right) - x$. Hàm số $g\left( x \right)$ đạt cực đại tại điểm nào sau đây?
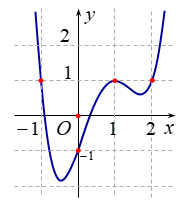
Ta có $g'\left( x \right) = f'\left( x \right) - 1$. Do đó đồ thị của hàm số $g'\left( x \right)$ có được bằng cách tịnh tiến đồ thị của hàm số $f'\left( x \right)$ đi xuống \(1\) đơn vị.
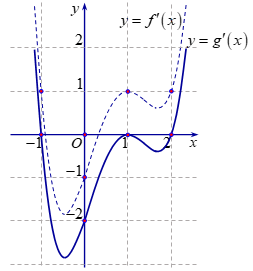
Quan sát đồ thị $g'\left( x \right)$ ta thấy \(g'\left( x \right)\) đổi dấu từ dương sang âm khi đi qua điểm \(x = - 1\).
Do đó $g\left( x \right)$ đạt cực đại tại $x = - 1$.
Một công ty bất động sản có $50$ căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá $2.000.000$ đồng một tháng thì mọi căn hộ đều có người thuê. Mỗi một căn hộ không thuê nữa (bỏ trống) thì công ty lại phải tăng số tiền thuê của những căn hộ còn lại thêm $50.000$ đồng. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
Ở tháng thu nhập của công ty cao nhất, gọi số căn hộ bị bỏ trống là \(x\) thì số tiền thuê mỗi phòng là \(2.000.000 + 50.000x\), khi đó số tiền thu được là
\(f\left( x \right) = \left( {2.000.000 + 50.000x} \right)\left( {50 - x} \right)\)\( = - 50.000{x^2} + 500.000x + 100.000.000\).
Ta cần tìm \(x \in \left( {0;\,50} \right)\) để \(f\left( x \right)\) lớn nhất.
Ta có \(f'\left( x \right) = - 100.000x + 500.000\), \(f'\left( x \right) = 0 \Leftrightarrow x = 5\)
Bảng biến thiên:
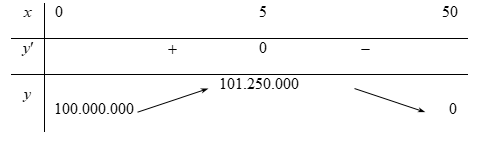
Vậy mỗi tháng lợi nhuận cao nhất thu được của công ty là $101.250.000$
Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số $y = {x^4} - 2m{x^2} + m - 1$ có ba điểm cực trị. Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng $1.$
Tập xác định \(D = \mathbb{R}\).
Ta có \(y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right)\).
Đồ thị hàm số có ba điểm cực trị $ \Leftrightarrow m \ge 0$
Khi đó: $y' = 4m{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt m \end{array} \right.$
Suy ra: Đồ thị hàm số có ba điểm cực trị là $A\left( {0;m - 1} \right)$ $B\left( { - \sqrt m ; - {m^2} + m - 1} \right)$, $C\left( {\sqrt m ; - {m^2} + m - 1} \right)$
Ta có: ${S_{\Delta ABC}} = \dfrac{1}{2}\left| {{y_B} - {y_A}} \right|.\left| {{x_C} - {x_B}} \right| = {m^2}\sqrt m $;
$AB = AC = \sqrt {{m^4} + m} $; $BC = 2\sqrt m $
Gọi \(R=1\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\)
Diện tích tam giác \(ABC\) là:
\({S_{\Delta ABC}} = \dfrac{{AB.AC.BC}}{{4R}} = \dfrac{{2\sqrt m \left( {{m^4} + m} \right)}}{4}\)
Suy ra \({m^2}\sqrt m = \dfrac{{2\sqrt m \left( {{m^4} + m} \right)}}{4} \Leftrightarrow 2m = {m^3} + 1\)
\( \Leftrightarrow \left( {m - 1} \right)\left( {{m^2} + m - 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\{m^2} + m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{{ - 1 + \sqrt 5 }}{2}\\m = \dfrac{{ - 1 - \sqrt 5 }}{2}\,\,\left( l \right)\end{array} \right.\)
Vậy: \(m = 1\) hoặc \(m = \dfrac{{ - 1 + \sqrt 5 }}{2}\)

