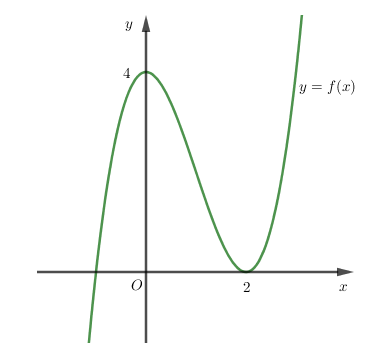
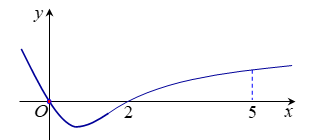
Cho hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị của hàm $y = f'\left( x \right)$ như hình vẽ. Biết rằng $f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)$. Giá trị nhỏ nhất và giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ {0;5} \right]$ lần lượt là:
Trả lời bởi giáo viên
Dựa vào đồ thị của hàm số $y = f'\left( x \right)$ ta có bảng biến thiên của hàm số $y = f\left( x \right)$:
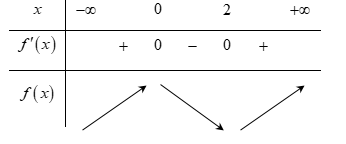
Quan sát bảng biến thiên ta thấy:
$f\left( 2 \right) < f\left( 3 \right) < f\left( 5 \right)$ và $f\left( 0 \right) > f\left( 2 \right)$
Mặt khác $f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow $$f\left( 3 \right) - f\left( 2 \right) = f\left( 5 \right) - f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)$
Vậy trên đoạn $\left[ {0;5} \right]$ hàm số $y = f\left( x \right)$ có: $f\left( 2 \right) < f\left( 0 \right) < f\left( 5 \right)$
Do đó:
+) \(GTNN\) của hàm số trên đoạn \(\left[ {0;5} \right]\) là \(f\left( 2 \right)\)
+) \(GTLN\) của hàm số trên đoạn \(\left[ {0;5} \right]\) là \(f\left( 5 \right)\)
Hướng dẫn giải:
- Lập bảng biến thiên của hàm số \(y = f\left( x \right)\)
- So sánh các giá trị \(f\left( 0 \right),f\left( 2 \right),f\left( 3 \right),f\left( 5 \right)\) rồi suy ra \(GTNN,GTLN\) của hàm số và kết luận.