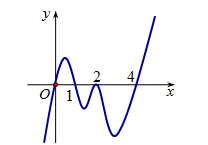
Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị $f'\left( x \right)$ như hình vẽ. Đặt $g\left( x \right) = f\left( x \right) - x$. Hàm số $g\left( x \right)$ đạt cực đại tại điểm nào sau đây?
Trả lời bởi giáo viên
Ta có $g'\left( x \right) = f'\left( x \right) - 1$. Do đó đồ thị của hàm số $g'\left( x \right)$ có được bằng cách tịnh tiến đồ thị của hàm số $f'\left( x \right)$ đi xuống \(1\) đơn vị.
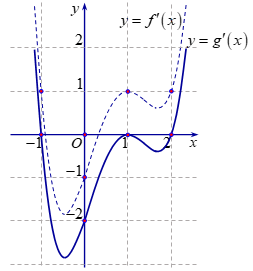
Quan sát đồ thị $g'\left( x \right)$ ta thấy \(g'\left( x \right)\) đổi dấu từ dương sang âm khi đi qua điểm \(x = - 1\).
Do đó $g\left( x \right)$ đạt cực đại tại $x = - 1$.
Hướng dẫn giải:
- Tính \(g'\left( x \right)\)
- Vẽ đồ thị hàm số \(y = g'\left( x \right)\) từ đồ thị hàm số \(y = f'\left( x \right)\)
- Tìm điểm cực đại dựa vào đồ thị hàm số và kết luận.