Một công ty bất động sản có $50$ căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá $2.000.000$ đồng một tháng thì mọi căn hộ đều có người thuê. Mỗi một căn hộ không thuê nữa (bỏ trống) thì công ty lại phải tăng số tiền thuê của những căn hộ còn lại thêm $50.000$ đồng. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
Trả lời bởi giáo viên
Ở tháng thu nhập của công ty cao nhất, gọi số căn hộ bị bỏ trống là \(x\) thì số tiền thuê mỗi phòng là \(2.000.000 + 50.000x\), khi đó số tiền thu được là
\(f\left( x \right) = \left( {2.000.000 + 50.000x} \right)\left( {50 - x} \right)\)\( = - 50.000{x^2} + 500.000x + 100.000.000\).
Ta cần tìm \(x \in \left( {0;\,50} \right)\) để \(f\left( x \right)\) lớn nhất.
Ta có \(f'\left( x \right) = - 100.000x + 500.000\), \(f'\left( x \right) = 0 \Leftrightarrow x = 5\)
Bảng biến thiên:
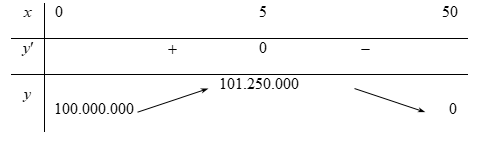
Vậy mỗi tháng lợi nhuận cao nhất thu được của công ty là $101.250.000$
Hướng dẫn giải:
- Lập phương trình hàm số lợi nhuận theo biến \(x\) là số căn hộ bị bỏ trống.
- Tìm \(GTLN\) của hàm số và kết luận.