Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên:
Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên \(\left( {0; + \infty } \right)\).
Hàm số nào dưới đây có tập xác định là \(\mathbb{R}\)?
Đáp án A: Hàm số \(y = {\log _2}\left( {x - 1} \right)\) xác định nếu \(x - 1 > 0 \Leftrightarrow x > 1\) nên loại A.
Đáp án B: Hàm số \(y = {\log _2}\left( {{x^2} - 1} \right)\) xác định nếu \({x^2} - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\) nên loại B.
Đáp án C: Hàm số \(y = {\log _2}\left( {{x^2} + 1} \right)\) xác định nếu \({x^2} + 1 > 0\) (luôn đúng).
Vậy hàm số xác định trên \(\mathbb{R}\).
Đáp án D: Hàm số \(y = {\log _2}\left( {\sqrt x } \right)\) xác định nếu \(\sqrt x > 0 \Leftrightarrow x > 0\) nên loại D.
Tính đạo hàm của hàm số $y = {\log _{2017}}x.$
Áp dụng \(\left( {{{\log }_a}x} \right)' = \dfrac{1}{{x.\ln a}}\), ta được $y' = \dfrac{1}{{x.\ln 2017}} = \dfrac{{{{\log }_{2017}}e}}{x}.$
Tính đạo hàm của hàm số $y = \log 2x.$
Ta có: \(\left[ {\log \left( {2x} \right)} \right]' = \dfrac{{\left( {2x} \right)'}}{{2x.\ln 10}} = \dfrac{1}{{x\ln 10}}\)
Tính đạo hàm của hàm số $y = {\log _2}\left( {2x + 1} \right).$
Áp dụng \(\left( {{{\log }_a}u} \right)' = \dfrac{{u'}}{{u.\ln a}}\), ta được $y' = \dfrac{{\left( {2x + 1} \right)'}}{{\left( {2x + 1} \right).\ln 2}} = \dfrac{2}{{\left( {2x + 1} \right).\ln 2}}.$
Cho giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{2\ln \left( {2x + 1} \right) - x}}{x} = \dfrac{a}{b}\) với \(a,b \in {\mathbb{N}^*}\) và \(\left( {a,b} \right) = 1\). Giá trị biểu thức \({a^2} + {b^2}\) là:
Ta có: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{2\ln \left( {2x + 1} \right) - x}}{x}\)\( = \mathop {\lim }\limits_{x \to 0} \left[ {\dfrac{{2\ln \left( {2x + 1} \right)}}{x} - 1} \right]\) \( = 2\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {2x + 1} \right)}}{x} - 1\) \( = 2\mathop {\lim }\limits_{x \to 0} \left[ {2.\dfrac{{\ln \left( {2x + 1} \right)}}{{2x}}} \right] - 1\) \( = 2.2 - 1 = 3\)
Do đó \(\dfrac{a}{b} = \dfrac{3}{1} \Rightarrow a = 3,b = 1\) (do \(a,b\) nguyên dương và \(\left( {a,b} \right) = 1\).
Vậy \({a^2} + {b^2} = {3^2} + {1^2} = 10\).
Hàm số nào sau đây đồng biến trên khoảng $\left( {0; + \infty } \right)$?
Trong các hàm số đã cho chỉ có hàm số $y = {\log _{\dfrac{e}{2}}}x$ đồng biến vì cơ số $a = \dfrac{e}{2} > 1$.
Hàm số nào sao đây nghịch biến trên \(\mathbb{R}\).
Hàm số $y = {2017^x}$ có TXĐ: \({\rm{D}} = \mathbb{R}\); cơ số \(2017 > 1\) nên đồng biến trên \(\mathbb{R}\).
Hàm số $y = {\log _{\dfrac{1}{2}}}x$ có TXĐ: \({\rm{D}} = \left( {0; + \infty } \right)\) nên không thỏa mãn.
Hàm số $y = {\log _{\sqrt 2 }}\left( {{x^2} + 1} \right)$ có TXĐ: \({\rm{D}} = \mathbb{R}\).
Ta có $y' = \dfrac{{2x}}{{\left( {{x^2} + 1} \right)\ln \sqrt 2 }}$ nên hàm số \(y = {\log _{\sqrt 2 }}\left( {{x^2} + 1} \right)\) đồng biến khi \(x > 0\), nghịch biến khi \(x < 0.\) Do đó C sai.
Hàm số $y = {\left( {\dfrac{\pi }{4}} \right)^x}$ có TXĐ: \({\rm{D}} = \mathbb{R}\); cơ số \(\dfrac{\pi }{4} < 1\) nên nghịch biến trên \(\mathbb{R}\).
Cho hai hàm số $y = f\left( x \right) = {\log _a}x$ và $y = g\left( x \right) = {a^x}$ \(\left( {0 < a \ne 1} \right)\). Xét các mệnh đề sau:
1) Đồ thị của hai hàm số $f\left( x \right)$ và $g\left( x \right)$ luôn cắt nhau tại một điểm.
2) Hàm số $f\left( x \right) + g\left( x \right)$ đồng biến khi \(a > 1\), nghịch biến khi \(0 < a < 1\).
3) Đồ thị hàm số $f\left( x \right)$ nhận trục $Oy$ làm tiệm cận.
4) Chỉ có đồ thị hàm số $f\left( x \right)$ có tiệm cận.
Hỏi có tất cả bao nhiêu mệnh đề đúng?
Chọn \(a = 2\) chẳng hạn, khi đó \(f\left( x \right)\) và \(g\left( x \right)\) cùng đồng biến.
Mà hai hàm cùng đồng biến thì không kết luận được số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) vì nó có thể vô nghiệm, hoặc có một nghiệm, hoặc có hai nghiệm,….Do đó 1) sai.
Tổng của hai hàm đồng biến là hàm đồng biến, tổng của hai hàm nghịch biến là hàm nghịch biến. Do đó 2) đúng.
Dựa vào lý thuyết, đồ thị hàm số $y = {\log _a}x$ nhận trục $Oy$ làm tiệm cận đứng. Do đó 3) đúng.
Đồ thị hàm số $y = {a^x}$ nhận trục $Ox$ làm tiệm cận ngang. Do đó 4) sai.
Vậy có các mệnh đề 2) và 3) đúng.
Hàm số \(y = {\log _2}\left( {{4^x} - {2^x} + m} \right)\) có tập xác định là \(\mathbb{R}\) khi
Bước 1: Tìm điều kiện để hàm số đã cho có tập xác định là \(\mathbb{R}\)
Điều kiện: \({4^x} - {2^x} + m > 0\).
Hàm số đã cho có tập xác định là \(\mathbb{R}\) khi và chỉ khi \({4^x} - {2^x} + m > 0(*)\forall x \in \mathbb{R}\).
Bước 2: Đặt \(t = {2^x}\) với \(t > 0\) và xét hàm số \(f(t) = {t^2} - t,\forall t > 0\)
Đặt \(t = {2^x}\) với \(t > 0\), khi đó bất phương trình \((*)\) trở thành \({t^2} - t + m > 0,\forall t > 0\).
Xét hàm số \(f(t) = {t^2} - t,\forall t > 0\) ta có \({f^\prime }(t) = 2t - 1;{f^\prime }(t) = 0 \Leftrightarrow t = \dfrac{1}{2}\).
Lập bảng biến thiên ta tìm được \({\min _{(0; + \infty )}}f(t) = f\left( {\dfrac{1}{2}} \right) = - \dfrac{1}{4}\).
Để bất phương trình \({t^2} - t + m > 0,\forall t > 0\) thì \( - m < - \dfrac{1}{4} \Leftrightarrow m > \dfrac{1}{4}\).
Cho hàm số \(y = {\log _2}\left( {3x} \right)\). Điểm nào dưới đây thuộc đồ thị hàm số?
Cho \(x = 1\) thì \(y = {\log _2}3\) hay đồ thị hàm số đi qua điểm \(\left( {1;{{\log }_2}3} \right)\) chứ không phải \(\left( {1;0} \right)\) nên A sai.
Cho \(x = 3\) thì \(y = {\log _2}{3^2} = {\log _3}9\) hay đồ thị hàm số đi qua điểm \(\left( {3;{{\log }_2}9} \right)\) nên B sai.
Cho \(x = 0\) thì \(3x = 0\) nên hàm số không xác định tại \(x = 0\), loại C.
Cho \(x = 2\) thì \(y = {\log _2}\left( {3.2} \right) = {\log _2}3 + {\log _2}2 = 1 + {\log _2}3\) hay đồ thị hàm số đi qua điểm \(\left( {2;1 + {{\log }_2}3} \right)\).
Điểm nào sau đây không thuộc đồ thị hàm số \(y = {\log _{\frac{1}{2}}}\left( {{x^2}} \right)\)?
Cho \(x = - 1 \Rightarrow y = {\log _{\frac{1}{2}}}\left( 1 \right) = 0\) nên đồ thị hàm số đi qua điểm \(\left( { - 1;0} \right)\).
Cho \(x = \pm 2 \Rightarrow y = {\log _{\frac{1}{2}}}\left( 4 \right) = - 2\) nên đồ thị hàm số đi qua điểm \(\left( {2; - 2} \right)\) và \(\left( { - 2; - 2} \right)\)
Cho \(x = \dfrac{1}{2}\) thì \(y = {\log _{\frac{1}{2}}}\dfrac{1}{4} = 2\) nên đồ thị hàm số đi qua điểm \(\left( {\dfrac{1}{2};2} \right)\) chứ không phải \(\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)\).
Cho hàm số $y = {\log _{\dfrac{1}{2}}}\left( {{3^{{x^3} - 3{x^2} + 2}}} \right)$. Mệnh đề nào sau đây đúng?
Viết lại $y = {\log _{\dfrac{1}{2}}}\left( {{3^{{x^3} - 3{x^2} + 2}}} \right) = \left( {{x^3} - 3{x^2} + 2} \right){\log _{\dfrac{1}{2}}}3 = - \left( {{x^3} - 3{x^2} + 2} \right).{\log _2}3$.
Nếu để ý thấy thì đây là hàm bậc ba thuần túy và có đạo hàm
$y' = - \left( {3{x^2} - 6x} \right).{\log _2}3 = - 3x\left( {x - 2} \right).{\log _2}3$$ \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.$
Lập bảng biến thiên, suy ra hàm số đồng biến trên khoảng $\left( {0;2} \right)$.
Cho các hàm số có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
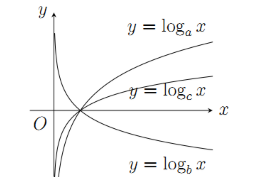
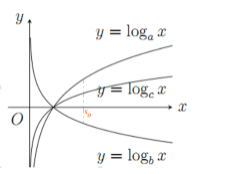
Nhận xét:
Hàm số \(y = {\log _a}x,\,\,y = {\log _c}x\) đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow a;\,\,c > 1\)
Hàm số \(y = {\log _b}x\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow b < 1\)
Lấy \({x_0} > 1\) (như hình vẽ). Ta có: \({\log _a}{x_0} > {\log _c}{x_0} \Rightarrow a < c\)
\( \Rightarrow b < 1 < a < c \Leftrightarrow b < a < c.\)
Cho hàm số \(y = x - \ln \left( {1 + x} \right)\). Khẳng định nào sau đây đúng?
TXĐ: \({\rm{D}} = \left( { - 1; + \infty } \right)\).
Đạo hàm \(y' = 1 - \dfrac{1}{{1 + x}} = \dfrac{x}{{x + 1}}\)\( \Rightarrow y' = 0 \Leftrightarrow x = 0\)
Bảng biến thiên
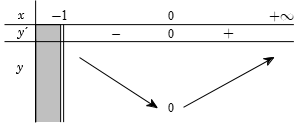
Từ bảng biến thiên, ta thấy hàm số giảm trên \(\left( { - 1;0} \right)\) và tăng trên \(\left( {0; + \infty } \right)\).
Cho hàm số $y = {\log _4}\left| x \right|$ \(\left( {x \ne 0} \right)\) có đồ thị $\left( C \right)$. Mệnh đề nào sau đây là đúng?
Tập xác định: ${\rm{D}} = \mathbb{R}\backslash \left\{ 0 \right\}$. Do đó A sai.
Với $x > 0$, ta có $y = {\log _4}x$ $ \Rightarrow $ hàm số đồng biến.
Với $x < 0$, ta có $y = {\log _4}\left( { - x} \right)$ $ \Rightarrow y' = \dfrac{{ - 1}}{{\left( { - x} \right)\ln 4}} < 0,{\rm{ }}\forall x < 0$ $ \Rightarrow y$ nghịch biến.
Do đó B sai.
Ta có $\left\{ \begin{array}{l}\forall x \in {\rm{D}} \Rightarrow \left( { - x} \right) \in {\rm{D}}\\y\left( { - x} \right) = {\log _4}\left| { - x} \right| = {\log _4}\left| x \right| = y\left( x \right)\end{array} \right.$ $ \Rightarrow $ hàm số $y = {\log _4}\left| x \right|$ chẵn trên tập xác định nên nhận $Oy$ làm trục đối xứng. Do đó C đúng.
Đáp án D sai. Ta có $\mathop {\lim }\limits_{x \to {0^ + }} {\log _4}\left| x \right| = \mathop {\lim }\limits_{x \to {0^ - }} {\log _4}\left| x \right| = - \infty $. Suy ra $x = 0$ là tiệm cận đứng.
Cho \(a\) là một số thực dương khác \(1\) và các mệnh đề sau:
1) Hàm số $y = {\log _a}x$ liên tục trên $\mathbb{R}$.
2) Nếu ${\log _a}\dfrac{2}{3} < 0$ thì $a > 1$.
3) ${\log _a}{x^2} = 2{\log _a}x$.
Hỏi có bao nhiêu mệnh đề đúng?
Hàm số $y = {\log _a}x$ xác định trên \(\left( {0; + \infty } \right)\). Do đó 1) sai.
Ta có ${\log _a}\dfrac{2}{3} < 0 \Leftrightarrow {\log _a}\dfrac{2}{3} < {\log _a}1 \Rightarrow a > 1$. Do đó 2) đúng.
Ta có ${\log _a}{x^2} = 2{\log _a}\left| x \right|$. Do đó 3) sai.
Vậy chỉ có 2) đúng.
Cho \(a\) là một số thực dương khác \(1\) và các mệnh đề sau:
1) Hàm số $y = \ln x$ là hàm số nghịch biến trên $\left( {0; + \infty } \right)$.
2) Trên khoảng $\left( {1;3} \right)$ hàm số $y = {\log _{\frac{1}{2}}}x$ nghịch biến.
3) Nếu $M > N > 0$ thì ${\log _a}M > {\log _a}N$.
4) Nếu ${\log _a}3 < 0$ thì $0 < a < 1$.
Hỏi có bao nhiêu mệnh đề đúng?
Vì cơ số \(e > 1 \Rightarrow y = \ln x\) đồng biến trên $\left( {0; + \infty } \right)$. Do đó 1) sai.
Hàm số $y = {\log _{\frac{1}{2}}}x$ có cơ số \(a = \dfrac{1}{2} \in \left( {0;1} \right)\) nên nghịch biến trên \(\mathbb{R}\), suy ra nghịch biến trên khoảng $\left( {1;3} \right)$. Do đó 2) đúng.
Nếu cơ số \(a \in \left( {0;1} \right)\) thì hàm số \(y = {\log _a}x\) nghịch biến. Vì vậy với $M > N > 0$, suy ra ${\log _a}M < {\log _a}N$. Do đó 3) sai.
Ta có ${\log _a}3 < 0 \Leftrightarrow {\log _a}3 < {\log _a}1 \Rightarrow 0 < a < 1$. Do đó 4) đúng.
Vậy có 2) và 4) đúng.
Cho hàm số \(f\left( x \right) = \ln \left( {{e^x} + \pi m} \right)\) thỏa mãn \(f'\left( {\ln 3} \right) = 3\). Mệnh đề nào sau đây đúng?
\(f\left( x \right) = \ln \left( {{e^x} + \pi m} \right) \Rightarrow f'\left( x \right) = \dfrac{{{e^x}}}{{{e^x} + \pi m}}\)
\(f'\left( {\ln 3} \right) = 3 \Leftrightarrow \dfrac{3}{{3 + \pi m}} = 3 \Leftrightarrow m = - \dfrac{2}{\pi } \approx - 0,64 \in \left( { - 1;0} \right)\).
Cho hàm số \(y = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \sqrt {1 + {x^2}} \). Mệnh đề nào sau đây sai?
Ta có \(x + \sqrt {{x^2} + 1} > x + \sqrt {{x^2}} = x + \left| x \right| \ge 0,{\rm{ }}\forall x \in \mathbb{R}.\)
Do đó hàm số có tập xác định là \({\rm{D}} = \mathbb{R}\). Suy ra C đúng.
Đạo hàm \(y' = \ln \left( {x + \sqrt {1 + {x^2}} } \right) + x.\dfrac{{1 + \dfrac{x}{{\sqrt {1 + {x^2}} }}}}{{x + \sqrt {1 + {x^2}} }} - \dfrac{x}{{\sqrt {1 + {x^2}} }} = \ln \left( {x + \sqrt {1 + {x^2}} } \right).\)Do đó A đúng.
Trên khoảng \(\left( {0; + \infty } \right)\), ta có \(\left\{ \begin{array}{l}\sqrt {1 + {x^2}} > 1\\1 - x < 1\end{array} \right. \Rightarrow \sqrt {1 + {x^2}} > 1 - x\) hay \(x + \sqrt {1 + {x^2}} > 1\).
Suy ra \(y' = \ln \left( {x + \sqrt {1 + {x^2}} } \right) > 0,{\rm{ }}\forall x \in \left( {0; + \infty } \right).\) Do đó B đúng, D sai.

