Trong không gian với hệ tọa độ Oxyz, cho \(M\left( {3;2;1} \right)\). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trục tâm tam giác ABC. Phương trình mặt phẳng (P) là:
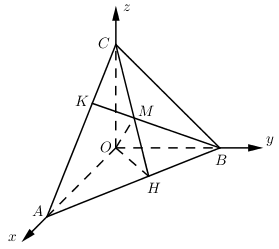
Gọi CH, BK lần lượt là các đường cao của tam giác ABC, \( \Rightarrow M = CH \cap BK\).
Ta có: \(\left\{ \begin{array}{l}AB \bot CH\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OCH} \right) \Rightarrow AB \bot OM\)
Chứng minh tương tự ta có \(AC \bot OM \Rightarrow OM \bot \left( {ABC} \right)\)
\(\overrightarrow {OM} = \left( {3;2;1} \right)\), suy ra mặt phẳng (ABC) đi qua \(M\left( {3;2;1} \right)\) và nhận \(\overrightarrow {OM} = \left( {3;2;1} \right)\) là 1 VTPT.
\(\begin{array}{l} \Rightarrow pt\left( {ABC} \right):\,\,3\left( {x - 3} \right) + 2\left( {y - 2} \right) + \left( {z - 1} \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 3x + 2y + z - 14 = 0\end{array}\)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( {1;0;0} \right),B\left( {0;2;0} \right),C\left( {0;0;3} \right).\) Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho OM.ON = 1. Biết rằng N luôn thuộc mặt cầu cố định. Viết phương trình mặt cầu đó?
Khi \(M \equiv A \Rightarrow OM = 1 \Rightarrow ON = 1,\,\,N \in OM \Rightarrow N\left( {1;0;0} \right)\), loại các đáp án A, C và D.
Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right):\;2x + 6y + z - 3 = 0\) cắt trục \(Oz\) và đường thẳng \(d:\;\dfrac{{x - 5}}{1} = \dfrac{y}{2} = \dfrac{{z - 6}}{{ - 1}}\) lần lượt tại \(A\) và \(B\). Phương trình mặt cầu đường kính \(AB\) là:
Phương trình trục \(Oz:\;\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right..\;\;\;A \in Oz \Rightarrow A\left( {0;\;0;\;t} \right).\)
Có \(\left( P \right) \cap Oz = \left\{ A \right\} \Rightarrow 2.0 + 6.0 + t - 3 = 0 \Leftrightarrow t = 3 \Rightarrow A\left( {0;\;0;\;3} \right).\)
\(d:\;\left\{ \begin{array}{l}x = 5 + t'\\y = 2t'\\z = 6 - t'\end{array} \right..\;\;B \in d \Rightarrow B\left( {5 + t';2t';6 - t'} \right).\)
Có $\left( P \right) \cap d = \left\{ B \right\} \Rightarrow 2\left( {5 + t'} \right) + 6.2t' + 6 - t' - 3 = 0 \Leftrightarrow t' = - 1 \Rightarrow B\left( {4; - 2;7} \right).$
Gọi \(I\) là trung điểm của \(AB \Rightarrow I\left( {2;\; - 1;\;5} \right).\)
Có \(\overrightarrow {AB} = \left( {4; - 2;\;4} \right) \Rightarrow AB = \sqrt {36} = 6 \Rightarrow IA = R = \dfrac{{AB}}{2} = 3.\)
Vậy đường tròn đường kính AB là: \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 5} \right)^2} = 9.\)
Trong không gian Oxyz, cho hai điểm \(A\left( { - 1;3; - 2} \right);\,\,B\left( { - 3;7; - 18} \right)\) và mặt phẳng \(\left( P \right):\,\,2x - y + z + 1 = 0\). Điểm \(M\left( {a;b;c} \right)\) thuộc (P) sao cho mặt phẳng (ABM) vuông góc với (P) và \(M{A^2} + M{B^2} = 246\). Tính \(S = a + b + c\).
\(M \in \left( P \right) \Rightarrow 2a - b + c + 1 = 0\)
Ta có:
\(\begin{array}{l}\overrightarrow {AB} = \left( { - 2;4; - 16} \right);\,\,\overrightarrow {AM} = \left( {a + 1;b - 3;c + 2} \right) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AM} } \right] = \left( {16b + 4c - 40;\,\, - 16a + 2c - 12;\,\, - 4a - 2b + 2} \right)\\{\overrightarrow n _{\left( P \right)}} = \left( {2; - 1;1} \right)\\ \Rightarrow 2\left( {16b + 4c - 40} \right) - \left( { - 16a + 2c - 12} \right) + \left( { - 4a - 2b + 2} \right) = 0\\ \Leftrightarrow 12a + 30b + 6c = 66 \Leftrightarrow 2a + 5b + c = 11\\M{A^2} + M{B^2} = 246\\ \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b - 3} \right)^2} + {\left( {c + 2} \right)^2} + {\left( {a + 3} \right)^2} + {\left( {b - 7} \right)^2} + {\left( {c + 18} \right)^2} = 246\\ \Leftrightarrow {a^2} + {b^2} + {c^2} + 4a - 10b + 20c + 75 = 0\end{array}\)
Khi đó ta có hệ phương trình \(\left\{ \begin{array}{l}2a - b + c = - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\2a + 5b + c = 11\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\{a^2} + {b^2} + {c^2} + 4a - 10b + 20c + 75 = 0\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)
\(\left( 1 \right),\left( 2 \right) \Rightarrow b = 2 \Rightarrow 2a - 2 + c = - 1 \Leftrightarrow 2a + c = 1 \Leftrightarrow c = 1 - 2a\)
Thay vào (3) ta có
\({a^2} + 4 + {\left( {1 - 2a} \right)^2} + 4a - 10.2 + 20\left( {1 - 2a} \right) + 75 = 0 \Leftrightarrow 5{a^2} - 40a + 80 = 0 \Leftrightarrow {a^2} - 8a + 16 = 0 \Leftrightarrow a = 4 \Rightarrow c = - 7\)
Vậy \(S = a + b + c = 4 + 2 - 7 = - 1\).
Trong không gian Oxyz, cho tam giác ABC có \(A\left( {2;3;3} \right)\), phương trình đường trung tuyến kẻ từ B là \(\dfrac{{x - 3}}{{ - 1}} = \dfrac{{y - 3}}{2} = \dfrac{{z - 2}}{{ - 1}}\), phương trình đường phân giác trong của góc C là \(\dfrac{{x - 2}}{2} = \dfrac{{y - 4}}{{ - 1}} = \dfrac{{z - 2}}{{ - 1}}\). Đường thẳng AB có vector chỉ phương là :
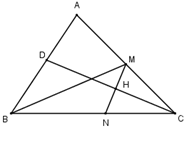
Tam giác ABC có trung tuyến BM và phân giác CD.
Gọi \(M\left( {3 - t;3 + 2t;2 - t} \right) \in BM\) là trung điểm của AC ta có \(C\left( {4 - 2t;3 + 4t;1 - 2t} \right) \in CD\).
\( \Rightarrow \dfrac{{2 - 2t}}{2} = \dfrac{{ - 1 + 4t}}{{ - 1}} = \dfrac{{ - 1 - 2t}}{{ - 1}} \Leftrightarrow \left\{ \begin{array}{l}2 - 2t = 2 - 4t\\2 - 2t = 2 + 4t\end{array} \right. \Leftrightarrow t = 0\)
\( \Rightarrow M\left( {3;3;2} \right);\,\,C\left( {4;3;1} \right)\)
Gọi H là hình chiếu của M trên CD ta có \(H\left( {2 + 2t;4 - t;2 - t} \right) \Rightarrow \overrightarrow {MH} = \left( { - 1 + 2t;1 - t; - t} \right)\)
\(\overrightarrow {MH} \bot \overrightarrow {{u_{CD}}} \Rightarrow 2\left( { - 1 + 2t} \right) - 1 + t + t = 0 \Leftrightarrow 6t = 3 \Leftrightarrow t = \dfrac{1}{2} \Rightarrow H\left( {3;\dfrac{7}{2};\dfrac{3}{2}} \right)\)
Gọi N là điểm đối xứng với M qua CD \( \Rightarrow H\) là trung điểm của MN \( \Rightarrow N\left( {3;4;1} \right) \Rightarrow \overrightarrow {CN} = \left( { - 1;1;0} \right)\)
Do CD là phân giác của góc C nên \(N \in BC\) , do đó phương trình đường thẳng CB là \(\left\{ \begin{array}{l}x = 4 - t'\\y = 3 + t'\\z = 1\end{array} \right.\)
Ta có \(B = BM \cap CB.\) Xét hệ phương trình
\(\left\{ \begin{array}{l}3 - t = 4 - t'\\3 + 2t = 3 + t'\\2 - t = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\t' = 2\end{array} \right. \Rightarrow B\left( {2;5;1} \right) \Rightarrow \overrightarrow {AB} = \left( {0;2; - 2} \right) = 2\left( {0;1; - 1} \right)\)
Vậy \(\overrightarrow {{u_4}} \left( {0;1; - 1} \right)\) là 1 VTCP của AB.
Trong không gian Oxyz, cho đường thẳng \(d:\,\,\dfrac{{x + 2}}{4} = \dfrac{{y - 1}}{{ - 4}} = \dfrac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):\,\,2x - y + 2z + 1 = 0\). Đường thẳng \(\Delta \) đi qua \(E\left( { - 2;1; - 2} \right)\), song song với (P) đồng thời tạo với d góc bé nhất. Biết rằng \(\Delta \) có một vector chỉ phương \(\overrightarrow u \left( {m;n;1} \right)\). Tính \(T = {m^2} - {n^2}\)
Ta có : \({\overrightarrow n _{\left( P \right)}} = \left( {2; - 1;2} \right)\)
Do \(\Delta //\left( P \right) \Rightarrow {\overrightarrow u _\Delta } \bot {\overrightarrow n _{\left( P \right)}} \Rightarrow 2m - n + 2 = 0 \Leftrightarrow n = 2m + 2\)
Ta có \(\cos \left( {\Delta ;d} \right) = \left| {\cos \left( {{{\overrightarrow u }_d};{{\overrightarrow u }_\Delta }} \right)} \right| = \dfrac{{\left| {4m - 4n + 3} \right|}}{{\sqrt {41} .\sqrt {{m^2} + {n^2} + 1} }} = \dfrac{{\left| {4m - 4\left( {2m + 2} \right) + 3} \right|}}{{\sqrt {41} .\sqrt {{m^2} + {{\left( {2m + 2} \right)}^2} + 1} }} = \dfrac{{\left| { - 4m - 5} \right|}}{{\sqrt {41} .\sqrt {5{m^2} + 8m + 5} }}\)
Để góc giữa \(\Delta \) và d là nhỏ nhất thì \(\cos \left( {{{\overrightarrow u }_d};{{\overrightarrow u }_\Delta }} \right)\,\max \)
\( \Rightarrow f\left( m \right) = \dfrac{{\left| { - 4m - 5} \right|}}{{\sqrt {5{m^2} + 8m + 5} }}\,\,\,\max \Rightarrow g\left( m \right) = {f^2}\left( m \right) = \dfrac{{16{m^2} + 40m + 25}}{{5{m^2} + 8m + 5}}\,\,\max \)
Có \(g'\left( x \right) = \dfrac{{\left( {32m + 40} \right)\left( {5{m^2} + 8m + 5} \right) - \left( {16{m^2} + 40m + 25} \right)\left( {10m + 8} \right)}}{{{{\left( {5{m^2} + 8m + 5} \right)}^2}}} = \dfrac{{ - 72{m^2} - 90m}}{{{{\left( {5{m^2} + 8m + 5} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - \dfrac{5}{4}\end{array} \right.\)
Lập BBT ta thấy \(\max g\left( m \right) = 5 \Leftrightarrow m = 0 \Rightarrow n = 2\)
Vậy \(T = {m^2} - {n^2} = - 4\).
Cho hình chóp S.ABCD có ABCD là hình bình hành, AB = 2a, BC = a, ABC = 1200 . Cạnh bên \(SD = a\sqrt 3 \) và SD vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Tính sin của góc tạo bởi SB và mặt phẳng (SAC).
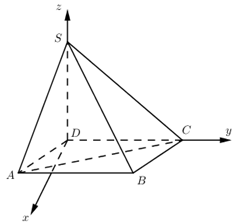
Gắn hệ trục tọa độ như hình vẽ ta có :
\(\begin{array}{l}D\left( {0;0;0} \right);\,\,S\left( {0;0;a\sqrt 3 } \right);\,\,C\left( {0;2a;0} \right);\,\,A\left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{{ - a}}{2};0} \right);\,\,B\left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{{3a}}{2};0} \right)\\ \Rightarrow \overrightarrow {SA} = \left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{{ - a}}{2}; - a\sqrt 3 } \right);\,\,\overrightarrow {AC} = \left( { - \dfrac{{a\sqrt 3 }}{2};\dfrac{{5a}}{2};0} \right) \Rightarrow \left[ {\overrightarrow {SA} ;\overrightarrow {AC} } \right] = \left( {\dfrac{{5\sqrt 3 {a^2}}}{2};\dfrac{{3{a^2}}}{2};\sqrt 3 {a^2}} \right) = {\overrightarrow n _{\left( {SAC} \right)}}\\\overrightarrow {SB} = \left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{{3a}}{2}; - a\sqrt 3 } \right)\\ \Rightarrow \left| {\cos \left( {{{\overrightarrow n }_{\left( {SAC} \right)}};\overrightarrow {SB} } \right)} \right| = \dfrac{{\left| {{{\overrightarrow n }_{\left( {SAC} \right)}}.\overrightarrow {SB} } \right|}}{{\left| {{{\overrightarrow n }_{\left( {SAC} \right)}}} \right|.\left| {\overrightarrow {SB} } \right|}} = \dfrac{3}{{\sqrt {144} }} = \dfrac{1}{4} = \sin \left( {SB;\left( {SAC} \right)} \right)\end{array}\)
Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện : tỉ số giữa diện tích của tam giác ABC và thể tích khối OABC bằng \(\dfrac{3}{2}\). Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng :
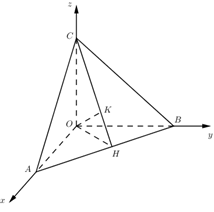
Kẻ \(OH \bot AB\,\,\left( {H \in AB} \right);\,\,OK \bot Ch\,\,\left( {K \in CH} \right)\) ta có
\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot OH\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OHC} \right) \Rightarrow AB \bot OK\\\left\{ \begin{array}{l}OK \bot AB\\OK \bot CH\end{array} \right. \Rightarrow OK \bot \left( {ABC} \right)\end{array}\)
Ta sẽ chứng minh OK không đổi, khi đó mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính OK.
Gọi \(A\left( {a;0;0} \right);\,\,B\left( {0;b;0} \right);\,\,C\left( {0;0;c} \right)\) ta có \({V_{ABC}} = \dfrac{1}{6}abc\).
\(\begin{array}{l}\overrightarrow {AB} = \left( { - a;b;0} \right);\,\,\overrightarrow {AC} = \left( { - a;0;c} \right) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {bc;ac;ab} \right) \Rightarrow {S_{ABC}} = \dfrac{1}{2}\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \\ \Rightarrow \dfrac{{{S_{ABC}}}}{{{V_{OABC}}}} = \dfrac{{\dfrac{1}{2}\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}{{\dfrac{1}{6}abc}} = \dfrac{3}{2}\\ \Leftrightarrow \sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} = \dfrac{1}{2}abc\\ \Leftrightarrow {a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2} = \dfrac{1}{4}{a^2}{b^2}{c^2}\\ \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}} = \dfrac{1}{4}\end{array}\)
Xét tam giác vuông OCK có \(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{1}{4} \Rightarrow OK = 2\)
Vậy mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính 2.
Trong không gian với hệ tọa độ $Oxyz,$ cho các điểm $A\left( {0;0; - \,2} \right),\,\,B\left( {4;0;0} \right).$ Mặt cầu $\left( S \right)$ có bán kính nhỏ nhất, đi qua $O,\,\,A,\,\,B$ có tâm là
Ta có $\overrightarrow {OA} = \left( {0;0; - \,2} \right),\,\,\overrightarrow {OB} = \left( {4;0;0} \right)$ suy ra $\overrightarrow {OA} .\overrightarrow {OB} = 0\,\, \Rightarrow \,\,\Delta \,OAB$ vuông tại $O.$
Do đó, mặt cầu $\left( S \right)$ có bán kính ${R_{\min }}$ và đi qua $O,\,\,A,\,\,B$ có tâm là trung điểm của $AB.$
Vậy tọa độ tâm mặt cầu là $I\left( {2;0; - \,1} \right).$
Trong không gian với hệ tọa độ $Oxyz,$ cho $A\left( { - \,3;0;0} \right),\,\,B\left( {0;0;3} \right),\,\,C\left( {0; - \,3;0} \right)$ và mặt phẳng $\left( P \right):x + y + z - 3 = 0.$ Tìm trên $\left( P \right)$ điểm $M$ sao cho $\left| {\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} } \right|$ nhỏ nhất.
Gọi $I\left( {a;b;c} \right)$ thỏa mãn $\overrightarrow {IA} + \overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 $ suy ra $I\left( { - \,3;3;3} \right).$ Khi đó $P = \left| {\overrightarrow {MI} } \right|.$
Để $I{M_{\min }}$$ \Leftrightarrow $$M$ là hình chiếu của $I$ trên $\left( P \right)$ mà $I \in \left( P \right) \Rightarrow M\left( { - \,3;3;3} \right).$

