Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện : tỉ số giữa diện tích của tam giác ABC và thể tích khối OABC bằng \(\dfrac{3}{2}\). Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng :
Trả lời bởi giáo viên
Đáp án đúng: b
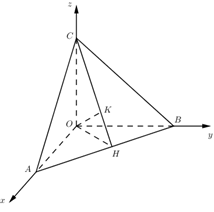
Kẻ \(OH \bot AB\,\,\left( {H \in AB} \right);\,\,OK \bot Ch\,\,\left( {K \in CH} \right)\) ta có
\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot OH\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OHC} \right) \Rightarrow AB \bot OK\\\left\{ \begin{array}{l}OK \bot AB\\OK \bot CH\end{array} \right. \Rightarrow OK \bot \left( {ABC} \right)\end{array}\)
Ta sẽ chứng minh OK không đổi, khi đó mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính OK.
Gọi \(A\left( {a;0;0} \right);\,\,B\left( {0;b;0} \right);\,\,C\left( {0;0;c} \right)\) ta có \({V_{ABC}} = \dfrac{1}{6}abc\).
\(\begin{array}{l}\overrightarrow {AB} = \left( { - a;b;0} \right);\,\,\overrightarrow {AC} = \left( { - a;0;c} \right) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {bc;ac;ab} \right) \Rightarrow {S_{ABC}} = \dfrac{1}{2}\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \\ \Rightarrow \dfrac{{{S_{ABC}}}}{{{V_{OABC}}}} = \dfrac{{\dfrac{1}{2}\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}{{\dfrac{1}{6}abc}} = \dfrac{3}{2}\\ \Leftrightarrow \sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} = \dfrac{1}{2}abc\\ \Leftrightarrow {a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2} = \dfrac{1}{4}{a^2}{b^2}{c^2}\\ \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}} = \dfrac{1}{4}\end{array}\)
Xét tam giác vuông OCK có \(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}} = \dfrac{1}{4} \Rightarrow OK = 2\)
Vậy mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính 2.
Hướng dẫn giải:
Chứng minh khoảng cách từ O đến (ABC) không đổi.
