Trong không gian Oxyz, cho tam giác ABC có \(A\left( {2;3;3} \right)\), phương trình đường trung tuyến kẻ từ B là \(\dfrac{{x - 3}}{{ - 1}} = \dfrac{{y - 3}}{2} = \dfrac{{z - 2}}{{ - 1}}\), phương trình đường phân giác trong của góc C là \(\dfrac{{x - 2}}{2} = \dfrac{{y - 4}}{{ - 1}} = \dfrac{{z - 2}}{{ - 1}}\). Đường thẳng AB có vector chỉ phương là :
Trả lời bởi giáo viên
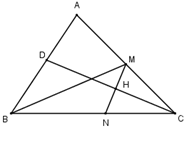
Tam giác ABC có trung tuyến BM và phân giác CD.
Gọi \(M\left( {3 - t;3 + 2t;2 - t} \right) \in BM\) là trung điểm của AC ta có \(C\left( {4 - 2t;3 + 4t;1 - 2t} \right) \in CD\).
\( \Rightarrow \dfrac{{2 - 2t}}{2} = \dfrac{{ - 1 + 4t}}{{ - 1}} = \dfrac{{ - 1 - 2t}}{{ - 1}} \Leftrightarrow \left\{ \begin{array}{l}2 - 2t = 2 - 4t\\2 - 2t = 2 + 4t\end{array} \right. \Leftrightarrow t = 0\)
\( \Rightarrow M\left( {3;3;2} \right);\,\,C\left( {4;3;1} \right)\)
Gọi H là hình chiếu của M trên CD ta có \(H\left( {2 + 2t;4 - t;2 - t} \right) \Rightarrow \overrightarrow {MH} = \left( { - 1 + 2t;1 - t; - t} \right)\)
\(\overrightarrow {MH} \bot \overrightarrow {{u_{CD}}} \Rightarrow 2\left( { - 1 + 2t} \right) - 1 + t + t = 0 \Leftrightarrow 6t = 3 \Leftrightarrow t = \dfrac{1}{2} \Rightarrow H\left( {3;\dfrac{7}{2};\dfrac{3}{2}} \right)\)
Gọi N là điểm đối xứng với M qua CD \( \Rightarrow H\) là trung điểm của MN \( \Rightarrow N\left( {3;4;1} \right) \Rightarrow \overrightarrow {CN} = \left( { - 1;1;0} \right)\)
Do CD là phân giác của góc C nên \(N \in BC\) , do đó phương trình đường thẳng CB là \(\left\{ \begin{array}{l}x = 4 - t'\\y = 3 + t'\\z = 1\end{array} \right.\)
Ta có \(B = BM \cap CB.\) Xét hệ phương trình
\(\left\{ \begin{array}{l}3 - t = 4 - t'\\3 + 2t = 3 + t'\\2 - t = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\t' = 2\end{array} \right. \Rightarrow B\left( {2;5;1} \right) \Rightarrow \overrightarrow {AB} = \left( {0;2; - 2} \right) = 2\left( {0;1; - 1} \right)\)
Vậy \(\overrightarrow {{u_4}} \left( {0;1; - 1} \right)\) là 1 VTCP của AB.
Hướng dẫn giải:
+) Tam giác ABC có trung tuyến BM và phân giác CD.
+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.
+) \(C \in CD \Rightarrow \) Tọa độ điểm C.
+) Tìm tọa độ điểm N đối xứng với M qua CD \( \Rightarrow N \in BC \Rightarrow \) Phương trình đường thẳng BC.
+) Tìm tọa độ điểm \(B = BM \cap BC\), khi đó mọi vector cùng phương với \(\overrightarrow {AB} \) đều là VTCP của AB.