Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ Oxyz, cho M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trục tâm tam giác ABC. Phương trình mặt phẳng (P) là:
Trả lời bởi giáo viên
Đáp án đúng: c
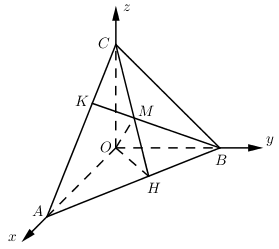
Gọi CH, BK lần lượt là các đường cao của tam giác ABC, ⇒M=CH∩BK.
Ta có: {AB⊥CHAB⊥OC⇒AB⊥(OCH)⇒AB⊥OM
Chứng minh tương tự ta có AC⊥OM⇒OM⊥(ABC)
→OM=(3;2;1), suy ra mặt phẳng (ABC) đi qua M(3;2;1) và nhận →OM=(3;2;1) là 1 VTPT.
⇒pt(ABC):3(x−3)+2(y−2)+(z−1)=0⇔3x+2y+z−14=0
Hướng dẫn giải:
Chứng minh OM⊥(ABC)⇒ Mặt phẳng (ABC) đi qua M và nhận →OM là 1 VTPT.