Tổng hợp câu hay và khó chương 7 phần 1

* Ta thấy \({z_A}.{z_B} < 0\) \( \Rightarrow A,\,\,B\) nằm khác phía với mặt phẳng \(\left( {Oxy} \right)\).

Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oxy} \right)\) \( \Rightarrow A'\left( {1; - 3; - 2} \right)\).

Khi đó \(P = \left| {AM - BN} \right| = \left| {A'M - BN} \right|\,\,\,\left( 1 \right)\).

Gọi \({A_1}\) là điểm sao cho \(\overrightarrow {A'{A_1}}  = \overrightarrow {MN} \).

Do \(MN = 4\) \( \Rightarrow {A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng 4.

Khi đó \(A'{A_1}NM\) là hình bình hành \( \Rightarrow A'M = {A_1}N\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow P = \left| {{A_1}N - BN} \right| \le {A_1}B\).

\( \Rightarrow {P_{\max }} = {A_1}B\) khi \({A_1},\,\,B,\,\,N\) thẳng hàng \(\left( {N = {A_1}B \cap \left( {Oxy} \right)} \right)\) và \({A_1}B\) lớn nhất khi \({A_1}\) ở vị trí \(\left( C \right)\) như hình vẽ.

Khi đó \({P_{\max }} = {A_1}{B_{\max }} = \sqrt {B{I^2} + I{A_1}^2} \).

Ta có \(\left\{ \begin{array}{l}BI = 2\\I{A_1} = IA' + A'{A_1} - 5 + 4 = 9\end{array} \right.\) .

\( \Rightarrow {P_{\max }} = \sqrt {{2^2} + {9^2}}  = \sqrt {85} \).

(Vị trí \(M,\,\,N\) để \({P_{\max }}\) như hình vẽ).

Ta thấy \({z_A}.{z_B} < 0\) nên \(A,B\) nằm khác phía so với mặt phẳng \(\left( {Oxy} \right).\)

Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oxy} \right)\)\( \Rightarrow A'\left( { - 2;1;3} \right)\).

Gọi \(H\) là hình chiếu của \(A'\) trên \(\left( {Oxy} \right) \Rightarrow H\left( { - 2;1;0} \right)\)

Gọi \(I\) là hình chiếu của \(B\) trên \(\left( {Oxy} \right) \Rightarrow I\left( {1; - 3;0} \right)\)

Suy ra \(HI = 5\)

Khi đó \(P = \left| {AM - BN} \right| = \left| {A'M - BN} \right|\)                                                   \(\left( 1 \right)\)

Gọi \({A_1}\) là điểm sao cho \(\overrightarrow {{A_1}A'}  = \overrightarrow {NM} \)

Do \(MN = 3\) nên \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng \(3.\)

Khi đó \({A_1}A'MN\) là hình bình hành \( \Rightarrow A'M = {A_1}N\)                             \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(P \le {A_1}B\)

\( \Rightarrow {P_{\max }} = {A_1}B\) khi \({A_1},B,N\) thẳng hàng với \(N\) là giao điểm của \({A_1}B\) và \(\left( {Oxy} \right)\)

Khi đó \({A_1}B\) có giá trị lớn nhất khi \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng \(3.\)

\({P_{\max }} = {A_1}B\) max \( = \sqrt {K{B^2} + {A_1}{K^2}} \)

Ta có: \(\left\{ \begin{array}{l}A'H = 3\\d\left( {B,\left( {Oxy} \right)} \right) = 2\end{array} \right. \Rightarrow BK = 1\)

Và \({A_1}K = A'{A_1} + A'K = {A_1}B' + HI = 3 + 5 = 8\)

\( \Rightarrow {P_{\max }} = \sqrt {{1^2} + {8^2}}  = \sqrt {65} \)

* Ta thấy \({z_A}.{z_B} < 0\) \( \Rightarrow A,\,\,B\) nằm khác phía với mặt phẳng \(\left( {Oxy} \right)\).

Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oxy} \right)\) \( \Rightarrow A'\left( {1; - 3;4} \right)\).

Khi đó \(P = \left| {AM - BN} \right| = \left| {A'M - BN} \right|\,\,\,\left( 1 \right)\).

Gọi \({A_1}\) là điểm sao cho \(\overrightarrow {A'{A_1}}  = \overrightarrow {MN} \).

Do \(MN = 2\) \( \Rightarrow {A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng 2.

Khi đó \(A'{A_1}NM\) là hình bình hành \( \Rightarrow A'M = {A_1}N\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow P = \left| {{A_1}N - BN} \right| \le {A_1}B\).

\( \Rightarrow {P_{\max }} = {A_1}B\) khi \({A_1},\,\,B,\,\,N\) thẳng hàng \(\left( {N = {A_1}B \cap \left( {Oxy} \right)} \right)\) và \({A_1}B\) lớn nhất khi \({A_1}\) ở vị trí \(\left( C \right)\) như hình vẽ.

Khi đó \({P_{\max }} = {A_1}{B_{\max }} = \sqrt {K{B^2} + {A_1}{K^2}} \).

Ta có \(\left\{ \begin{array}{l}A'H = 4\\d\left( {B;\left( {Oxy} \right)} \right) = 2\end{array} \right. \Rightarrow BK = 2\) và \({A_1}K = A'{A_1} + A'K = 2 + 5 = 7\).

\( \Rightarrow {P_{\max }} = \sqrt {{2^2} + {7^2}}  = \sqrt {53} \).

(Vị trí \(M,\,\,N\) để \({P_{\max }}\) như hình vẽ).

Ta thấy \({z_A}.{z_B} < 0\) nên \(A,B\) nằm khác phía so với mặt phẳng \(\left( {Oxy} \right).\)

Gọi \(B'\) là điểm đối xứng với \(B\) qua \(\left( {Oxy} \right)\)\( \Rightarrow B'\left( { - 2;1;3} \right)\).

Gọi \(H\) là hình chiếu của \(B'\) trên \(\left( {Oxy} \right) \Rightarrow H\left( { - 2;1;0} \right)\)

Gọi \(I\) là hình chiếu của \(A\) trên \(\left( {Oxy} \right) \Rightarrow I\left( {1; - 3;0} \right)\)

Suy ra \(HI = 5\)

Khi đó \(P = \left| {AM - BN} \right| = \left| {AM - B'N} \right|\)                                                   \(\left( 1 \right)\)

Gọi \({A_1}\) là điểm sao cho \(\overrightarrow {{A_1}B'}  = \overrightarrow {MN} \)

Do \(MN = 1\) nên \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(B'\) bán kính bằng \(1.\)

Khi đó \({A_1}B'NM\) là hình bình hành \( \Rightarrow B'N = {A_1}M\)                             \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(P = \left| {{A_1}M - AM} \right| \le {A_1}A\)

\( \Rightarrow {P_{\max }} = {A_1}A\) khi \({A_1},A,M\) thẳng hàng với \(M\) là giao điểm của \({A_1}A\) và \(\left( {Oxy} \right)\)

Khi đó \({A_1}A\) có giá trị lớn nhất khi \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(B'\) bán kính bằng \(1.\)

\({P_{\max }} = {A_1}A\) max \( = \sqrt {K{A^2} + {A_1}{K^2}} \)

Ta có: \(\left\{ \begin{array}{l}B'H = 3\\d\left( {A,\left( {Oxy} \right)} \right) = 2\end{array} \right. \Rightarrow AK = 1\)

Và \({A_1}K = B'{A_1} + B'K = {A_1}B' + HI = 1 + 5 = 6\)

\( \Rightarrow {P_{\max }} = \sqrt {{1^2} + {6^2}}  = \sqrt {37} \)

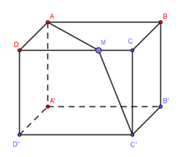
$AB = \sqrt 3 ,\,\,AD = \sqrt 6 ,\,\,AA' = 2\sqrt 2 $

Gọi độ dài đoạn $DM = x,\,\,\left( {0 \le x \le \sqrt 3 } \right)$. Khi đó, tổng các khoảng cách: 

$AM + MC' = \sqrt {6 + {x^2}}  + \sqrt {8 + {{\left( {\sqrt 3  - x} \right)}^2}}  \ge \sqrt {{{\left( {\sqrt 6  + \sqrt 8 } \right)}^2} + {{\left( {x + \sqrt 3  - x} \right)}^2}}  = \sqrt {6 + 8\sqrt 3  + 8 + 3}  = \sqrt {17 + 8\sqrt 3 } $

$ \Rightarrow AM + MC'\,\,\min  = \sqrt {17 + 8\sqrt 3 } $ khi và chỉ khi $\dfrac{{\sqrt 6 }}{{\sqrt 8 }} = \dfrac{x}{{\sqrt 3  - x}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow 2x = 3 - \sqrt 3 x \Leftrightarrow x = \dfrac{3}{{2 + \sqrt 3 }} = 6 - 3\sqrt 3 $.

$A(0; - 1;2),\,\,B(1;1;2) \Rightarrow \overrightarrow {AB} \left( {1;2;0} \right) \Rightarrow AB:\left\{ \begin{array}{l}x = {t_1}\\y =  - 1 + 2{t_1}\\z = 2\end{array} \right.$

$\left( d \right):\,\,\dfrac{{x + 1}}{1} = \dfrac{y}{1} = \dfrac{{z - 1}}{1} \Leftrightarrow \left( d \right):\left\{ \begin{array}{l}x =  - 1 + t\\y = t\\z = 1 + t\end{array} \right.$

Mà M thuộc d nên khoảng cách $d{(M;AB)_{\min }} = d(d;AB) = $ Độ dài đoạn vuông góc chung của d và AB.

Gọi HK là đoạn vuông góc chung của AB và d $\left( {H \in d,\,\,K \in AB} \right)$

Vì $H \in d,\,\,K \in AB$ nên, giả sử $H\left( { - 1 + t;\,\,\,t\,\,;1 + t} \right),\,K\left( {{t_1}; - 1 + 2{t_1};2} \right) \Rightarrow \overrightarrow {HK}  = \left( {{t_1} - t + 1;2{t_1} - t - 1;1 - t} \right)$

HK là đoạn vuông góc chung của AB và d$ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {HK}  \bot \overrightarrow {{u_{AB}}} \\\overrightarrow {HK}  \bot \overrightarrow {{u_d}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {{t_1} - t + 1} \right).1 + \left( {2{t_1} - t - 1} \right).2 + \left( {1 - t} \right)0 = 0\\\left( {{t_1} - t + 1} \right).1 + \left( {2{t_1} - t - 1} \right).1 + \left( {1 - t} \right).1 = 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}5{t_1} - 3t = 1\\3{t_1} - 3t =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 1\\t = \dfrac{4}{3}\end{array} \right. \Rightarrow H\left( {\dfrac{1}{3};\dfrac{4}{3};\dfrac{7}{3}} \right)$

Diện tích tam giác MAB nhỏ nhất khi M(a;b;c) trùng$H\left( {\dfrac{1}{3};\dfrac{4}{3};\dfrac{7}{3}} \right)$.

$ \Rightarrow a = \dfrac{1}{3},\,b = \dfrac{4}{3},\,c = \dfrac{7}{3} \Rightarrow T = \dfrac{1}{3} + 2.\dfrac{4}{3} + 3.\dfrac{7}{3} = 10$

+) Xác định điểm $I(a;b;c)$ sao cho: $2\overrightarrow {IA}  + 3\overrightarrow {IB}  - 4\overrightarrow {IC}  = \overrightarrow 0 $:

Ta có:$\overrightarrow {IA}  = \left( {2 - a;1 - b; - c} \right),\,\,\overrightarrow {IB}  = \left( { - a;2 - b;1 - c} \right),\,\,\overrightarrow {IC}  = \left( {1 - a;3 - b; - 1 - c} \right)$

$ \Rightarrow \left\{ \begin{array}{l}2\left( {2 - a} \right) + 3\left( { - a} \right) - 4\left( {1 - a} \right) = 0\\2\left( {1 - b} \right) + 3\left( {2 - b} \right) - 4\left( {3 - b} \right) = 0\\2\left( { - c} \right) + 3\left( {1 - c} \right) - 4\left( { - 1 - c} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b =  - 4\\c = 7\end{array} \right. \Rightarrow I(0; - 4;7)$

Khi đó: $\left| {2\overrightarrow {MA}  + 3\overrightarrow {MB}  - 4\overrightarrow {MC} } \right| = \left| {2\overrightarrow {MI}  + 2\overrightarrow {IA}  + 3\overrightarrow {MI}  + 3\overrightarrow {IB}  - 4\overrightarrow {MI}  - 4\overrightarrow {IC} } \right| = \left| {\overrightarrow {MI}  + \underbrace {\left( {2\overrightarrow {IA}  + 3\overrightarrow {IB}  - 4\overrightarrow {IC} } \right)}_{\overrightarrow 0 }} \right| = MI$, $ \Rightarrow \left| {2\overrightarrow {MA}  + 3\overrightarrow {MB}  - 4\overrightarrow {MC} } \right|$ đạt GTNN khi và chỉ khi MI ngắn nhất

$ \Leftrightarrow $M là chân đường vuông góc kẻ từ I đến mặt phẳng $\left( \alpha  \right)$.

+) Xác đinh tọa độ điểm $H$ là chân đường vuông góc kẻ từ $I(0; - 4;7)$ đến mặt phẳng $\left( \alpha  \right):2x + y - 2z + 9 = 0$.

Đường thẳng IH nhận $\overrightarrow {{n_{\left( \alpha  \right)}}} \left( {2;1; - 2} \right)$ là VTCP, phương trình đường thẳng IH:  $\left\{ \begin{array}{l}x = 2t\\y =  - 4 + t\\z = 7 - 2t\end{array} \right.$

$\begin{array}{l}H \in IH \Rightarrow H\left( {2t; - 4 + t;7 - 2t} \right)\\H \in \left( \alpha  \right) \Rightarrow 2\left( {2t} \right) + \left( { - 4 + t} \right) - 2\left( {7 - 2t} \right) + 9 = 0 \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1 \Rightarrow H\left( {2; - 3;5} \right)\end{array}$

Vậy, điểm M cần tìm có tọa độ $M\left( {2; - 3;5} \right) \Rightarrow {x_M} + {y_M} + {z_M} = 4$.

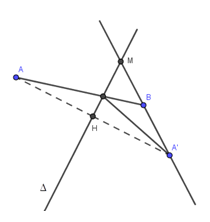
+) Chứng minh $A, B,\Delta $ đồng phẳng:

Gọi $\left( \alpha  \right)$ là mặt phẳng qua A và chứa $\Delta $ ($\Delta $ đi qua $C(0;1;0)$ và nhận $\overrightarrow u (1;1;1)$ là VTCP)

$\overrightarrow {AC}  = \left( { - 1; - 1;5} \right)$

 $\left( \alpha  \right)$ có 1 VTPT  $\overrightarrow n  = \left[ {\overrightarrow u ;\overrightarrow {AC} } \right] = (6; - 6;0)$.

Phương trình mặt phẳng $\left( \alpha  \right)$:  $6(x - 1) - 6(y - 2) + 0(z + 5) = 0 \Leftrightarrow x - y + 1 = 0$

Ta có:  $\,B( - 1;0;2);\,\,\, - 1 + 0 + 1 = 0 \Rightarrow B \in \left( \alpha  \right)$

$ \Rightarrow $ A, B, $\Delta $ đồng phẳng.

+) Tìm giao điểm của $M$ của $AB $ và $\Delta $:

$\Delta :\dfrac{x}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{1}$ có PTTS : $\left\{ \begin{array}{l}x = t\\y = 1 + t\\z = t\end{array} \right.$ , $M \in \Delta  \Rightarrow M(t;1 + t;t)$

$\,\overrightarrow {AB} ( - 2; - 2;7)$, $\overrightarrow {AM} \left( {t - 1;t - 1;t + 5} \right)$

$A,M,B$ thẳng hàng  $ \Rightarrow \overrightarrow {AM} //\overrightarrow {AB}  \Rightarrow \dfrac{{t - 1}}{{ - 2}} = \dfrac{{t - 1}}{{ - 2}} = \dfrac{{t + 5}}{7} \Leftrightarrow t =  - \dfrac{1}{3} \Rightarrow M\left( {\dfrac{{ - 1}}{3};\dfrac{2}{3}; - \dfrac{1}{3}} \right)$

 Mặt khác, $\overrightarrow {AM} \left( { - \dfrac{4}{3}; - \dfrac{4}{3};\dfrac{{14}}{3}} \right);\,\,\overrightarrow {BM} \left( {\dfrac{2}{3};\dfrac{2}{3};\dfrac{{ - 7}}{3}} \right) \Rightarrow \overrightarrow {AM}  =  - 2\overrightarrow {BM}  \Rightarrow $ M nằm giữa A và B, suy ra, trong $\left( \alpha  \right)$, A và B nằm khác phía so với đường thẳng $\Delta $.

Gọi A’ là điểm đối xứng với A qua B. Khi đó, $\left| {MA - MB} \right| = \left| {MA' - MB} \right| \le A'B$, ${\left| {MA' - MB} \right|_{max}} = A'B$ khi và chỉ khi M là giao điểm của A’B và đường thẳng $\Delta $ (điểm M như trên là tồn tại).

+) Tìm tọa độ điểm A’:

Gọi $\left( \beta  \right)$ là mặt phẳng qua A và vuông góc $\Delta $, khi đó, $\left( \beta  \right)$ nhận $\overrightarrow {{u_\Delta }} (1;1;1)$ là 1 VTPT.

Phương trình mặt phẳng  $\left( \beta  \right)$:

$1.(x - 1) + 1.(y - 2) + 1.(z + 5) = 0 \Leftrightarrow x + y + z + 2 = 0$

$H \in \Delta  \Rightarrow $Gọi $H(m;1 + m;m)$

$H \in \left( \beta  \right) \Rightarrow m + 1 + m + m + 2 = 0 \Leftrightarrow m =  - 1$$ \Rightarrow H( - 1;0; - 1)$

 H là trung điểm của AA’ $ \Rightarrow \left\{ \begin{array}{l}{x_H} = \dfrac{{{x_A} + {x_{A'}}}}{2}\\{y_H} = \dfrac{{{y_A} + {y_{A'}}}}{2}\\{z_H} = \dfrac{{{z_A} + {z_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} =  - 3\\{y_{A'}} =  - 2\\{z_{A'}} = 3\end{array} \right.$

Độ dài đoạn A’B: $A'B = \sqrt {{{( - 1 + 3)}^2} + {{(0 + 2)}^2} + {{(2 - 3)}^2}}  = 3$

Vậy,  ${T_{max}} = 3$

Ta có: \(\overrightarrow {IA}  = \left( {1;\;1; - 1} \right) \Rightarrow R = IA = \sqrt 3 .\)

Lại có: \(A:\;\;R = IA = \dfrac{{\sqrt {A{B^2} + A{C^2} + A{D^2}} }}{2} = \sqrt 3  \Rightarrow A{B^2} + A{C^2} + A{D^2} = 12.\)

Áp dụng bất đẳng thức Cauchy ta có: \(A{B^2} + A{C^2} + A{D^2} \ge 3\sqrt[3]{{A{B^2}.A{C^2}.A{D^2}}}\)

\(\begin{array}{l} \Leftrightarrow \sqrt[3]{{A{B^2}.A{C^2}.A{D^2}}} \le 4 \Leftrightarrow AB.AC.AD \le 8.\\ \Rightarrow {V_{ABCD}} = \dfrac{1}{6}AB.AC.AD \le \dfrac{1}{6}.8 = \dfrac{4}{3}.\end{array}\)

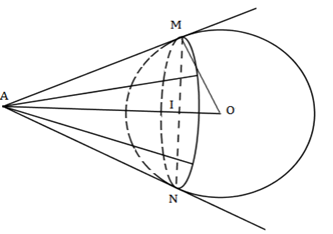
Ta có\(\left( S \right)\) có tâm \(O\left( {2;\;3; - 1} \right)\) và bán kính \(R = 4.\)

\(\overrightarrow {AO}  = \left( {3;\;4;\;0} \right) \Rightarrow OA = 5.\)

Tập hợp các điểm \(M\) là đường tròn tâm \(I\) bán kính \(IM.\)

Gọi \(\left( \alpha  \right)\) là mặt phẳng chứa đường tròn đó.

Khi đó ta có \(OA \bot \left( \alpha  \right) \Rightarrow \left( \alpha  \right)\) nhận \(\overrightarrow {AO}  = \left( {3;\;4;\;0} \right)\) làm VTPT.

\( \Rightarrow \left( \alpha  \right):\;\;3x + 4y + a = 0.\)

Áp dụng hệ thức lượng trong tam giác vuông \(OAM\) có đường cao \(MI\) ta có:

\(\begin{array}{l}OI = \dfrac{{O{M^2}}}{{OA}} = \dfrac{{{4^2}}}{5} = \dfrac{{16}}{5} = d\left( {O;\;\left( \alpha  \right)} \right).\\ \Rightarrow \dfrac{{16}}{5} = \dfrac{{\left| {2.3 + 4.3 + a} \right|}}{5} \Leftrightarrow \left| {18 + a} \right| = 16 \Leftrightarrow \left[ \begin{array}{l}a =  - 2\\a =  - 34\end{array} \right..\\ \Rightarrow \left[ \begin{array}{l}\left( \alpha  \right):\;\;3x + 4y - 2 = 0\\\left( \alpha  \right):\;3x + 4y - 34 = 0\end{array} \right..\end{array}\)

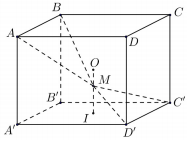
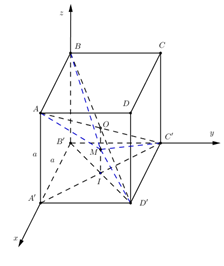
Gọi hình lập phương có cạnh là \(a.\)

Xét hệ trục tọa độ như hình vẽ ta có:

\(\begin{array}{l}B'\left( {0;\;0;\;0} \right),\;\;A'\left( {a;\;0;\;0} \right),\;C'\left( {0;\;a;\;0} \right),\;D'\left( {a;\;a;\;0} \right),\\A\left( {a;\;0;\;a} \right),\;I\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;0} \right),\;B\left( {0;\;0;\;a} \right),\;O\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{a}{2}} \right).\\ \Rightarrow \overrightarrow {OI}  = \left( {0;\;0;\;\dfrac{a}{2}} \right) \Rightarrow \overrightarrow {OM}  = \dfrac{1}{3}\overrightarrow {OI}  = \left( {0;\;0;\;\dfrac{a}{6}} \right).\\ \Rightarrow \left\{ \begin{array}{l}{x_M} - {x_O} = 0\\{y_M} - {y_O} = 0\\{z_M} - {z_O} = \dfrac{a}{6}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{a}{2}\\{y_M} = \dfrac{a}{2}\\{z_M} = \dfrac{{2a}}{3}\end{array} \right. \Rightarrow M\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{{2a}}{3}} \right).\end{array}\)

\(\begin{array}{l} \Rightarrow \overrightarrow {MA}  = \left( {\dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MB}  = \left( { - \dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MC'}  = \left( { - \dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right),\;\overrightarrow {MD'}  = \left( {\dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right).\\ \Rightarrow {\overrightarrow n _{\left( {MAB} \right)}} = \left[ {\overrightarrow {MA} ,\;\overrightarrow {MB} } \right] = \left( {0; - \dfrac{{{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) =  - {a^2}\left( {0;\;\dfrac{1}{3};\;\dfrac{1}{2}} \right).\\{\overrightarrow n _{\left( {MC'D'} \right)}} = \left[ {\overrightarrow {MC'} ,\;\overrightarrow {MD'} } \right] = \left( {0; - \dfrac{{2{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) =  - {a^2}\left( {0;\;\dfrac{2}{3};\;\dfrac{1}{2}} \right).\end{array}\)

Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {M'C'D'} \right).\)

$\begin{array}{l} \Rightarrow \cos \alpha  = \dfrac{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}.{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}}{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}} \right|.\left| {{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}} = \dfrac{{\left| {\dfrac{1}{3}.\dfrac{2}{3} + \dfrac{1}{2}.\dfrac{1}{2}} \right|}}{{\sqrt {\dfrac{1}{9} + \dfrac{1}{4}} .\sqrt {\dfrac{4}{9} + \dfrac{1}{4}} }} = \dfrac{{17\sqrt {13} }}{{65}}.\\ \Rightarrow sin\alpha  = \sqrt {1 - {{\cos }^2}\alpha }  = \dfrac{{6\sqrt {13} }}{{65}}.\end{array}$

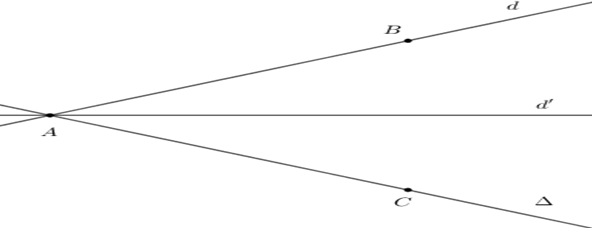
Ta có: \(\overrightarrow {{u_d}}  = \left( {3;\;4;\;0} \right)\) và \(d\) đi qua \(A\left( {1;\;1;\;1} \right).\)

\( \Rightarrow d \cap \Delta  = A\left( {1;\;1;\;1} \right).\)

Phương trình đường thẳng \(\Delta :\;\;\left\{ \begin{array}{l}x = 1 - 2t\\y = 1 + t\\z = 1 + 2t\end{array} \right..\)

Chọn \(B\left( {4;\;5;\;1} \right)\) là một điểm thuộc đường thẳng \(d.\)

Ta có: \(\overrightarrow {AB}  = \left( {3;\;4;\;0} \right) \Rightarrow AB = 5.\)

Lấy điểm \(C\left( {1 - 2t;\;1 + t;\;1 + 2t} \right) \in \Delta \) sao cho \(AB = AC.\)

\( \Rightarrow {\left( { - 2t} \right)^2} + {t^2} + {\left( {2t} \right)^2} = 25 \Leftrightarrow {t^2} = \dfrac{{25}}{9} \Leftrightarrow t =  \pm \dfrac{5}{3}.\)

+) Với \(t = \dfrac{5}{3} \Rightarrow C\left( { - \dfrac{7}{3};\;\dfrac{8}{3};\;\dfrac{{13}}{3}} \right) \Rightarrow \overrightarrow {AC}  = \left( { - \dfrac{{10}}{3};\;\dfrac{5}{3};\;\dfrac{{10}}{3}} \right).\)

Khi đó ta có: \(\cos \left( {d,\;\Delta } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \dfrac{{ - \dfrac{{10}}{3}}}{{5.5}} =  - \dfrac{2}{{15}} < 0 \Rightarrow \angle \left( {d;\;\Delta } \right)\) là góc tù.

+) Với \(t =  - \dfrac{5}{3} \Rightarrow C\left( {\dfrac{{13}}{3}; - \dfrac{2}{3}; - \dfrac{7}{3}} \right) \Rightarrow \overrightarrow {AC}  = \left( {\dfrac{{10}}{3}; - \dfrac{5}{3}; - \dfrac{{10}}{3}} \right).\)

Khi đó ta có: \(\cos \left( {d,\;\Delta } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \dfrac{{\dfrac{{10}}{3}}}{{5.5}} = \dfrac{2}{{15}} > 0 \Rightarrow \angle \left( {d;\;\Delta } \right)\) là góc nhọn nên ta cần lập phương trình đường phân giác trong TH này.

Ta có VTCP của đường phân giác của góc tạo bởi \(d\) và \(\Delta \) là: \(\overrightarrow u  = \overrightarrow {AB}  + \overrightarrow {AC}  = \left( {\dfrac{{19}}{3};\;\dfrac{7}{3};\; - \dfrac{{10}}{3}} \right) = \dfrac{1}{3}\left( {19;\;7;\; - 10} \right).\)

Khi đó phương trình đường phân giác \(d'\)  đi qua \(A\left( {1;\;1;\;1} \right)\) và có VTCP \(\overrightarrow u  = \left( {19;\;7; - 10} \right)\) là: \(\left\{ \begin{array}{l}x = 1 + 19t\\y = 1 + 7t\\z = 1 - 10t\end{array} \right..\)

Với \(t =  - 1\) ta có: \(I\left( { - 18; - 6;\;11} \right) \in d'.\)

Vậy đường thẳng \(d':\;\left\{ \begin{array}{l}x =  - 18 + 19t\\y =  - 6 + 7t\\z = 11 - 10t\end{array} \right..\)

Gọi $A\left( {a;0;0} \right),\,\,B\left( {0;b;0} \right),\,\,C\left( {0;0;c} \right)$$ \Rightarrow $ Phương trình mặt phẳng $\left( P \right):\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1.$

Vì $OA,\,\,OB,\,\,OC$ đôi một vuông góc $ \Rightarrow $ Thể tích khối chóp $O.ABC$ là $V = \dfrac{1}{6}OA.OB.OC = \dfrac{{abc}}{6}.$

Điểm $M \in \left( P \right)$ suy ra $1 = \dfrac{1}{a} + \dfrac{2}{b} + \dfrac{3}{c} \ge 3\sqrt[3]{{\dfrac{1}{a}.\dfrac{2}{b}.\dfrac{3}{c}}} \Leftrightarrow 1 \ge {3^3}.\dfrac{6}{{abc}} \Rightarrow abc \ge 162 \Rightarrow V \ge 27.$

Dấu bằng xảy ra khi và chỉ khi $\dfrac{1}{a} = \dfrac{2}{b} = \dfrac{3}{c} = \dfrac{1}{3} \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 6\\c = 9\end{array} \right..$ Vậy $\left( P \right):\dfrac{x}{3} + \dfrac{y}{6} + \dfrac{z}{9} = 1.$

Ta có \(\overrightarrow {AB}  = \left( {2; - 2;6} \right)\); \(\overrightarrow {{u_d}}  = \left( {2; - 1;2} \right)\), d đi qua điểm \(M\left( { - 1;1;0} \right)\)

\( \Rightarrow \left[ {\overrightarrow {AB} .\overrightarrow {{u_d}} } \right].\overrightarrow {AM}  \ne 0 \Rightarrow AB\) và d chéo nhau.

Ta có \({C_{MAB}} = MA + MB + AB\). Do AB không đổi nên \({C_{MAB\,\,\min }} \Leftrightarrow {\left( {MA + MB} \right)_{\min }}\).

Do AB và d chéo nhau nên \(MA + MB\mathop  \ge \limits^{Cauchy} 2\sqrt {MA.MB}  \Leftrightarrow {\left( {MA + MB} \right)_{\min }} \Leftrightarrow MA = MB\).

\( \Rightarrow M \in \) mặt phẳng trung trực của AB đi qua trung điểm \(I\left( {2;4;3} \right)\) của AB và nhận \(\left( {1; - 1;3} \right)\) là 1 VTPT.

\( \Rightarrow M \in \left( P \right):\,\,x - y + 3z - 7 = 0\).

\( \Rightarrow M \in \left( d \right) \Rightarrow M\left( { - 1 + 2t;1 - t;2t} \right).\)

Thay vào mặt phẳng (P) \( \Rightarrow  - 1 + 2t - 1 + t + 6t - 7 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {1;0;2} \right) \Rightarrow MA = MB = \sqrt {29} \)

\(AB = 2\sqrt {11}  \Rightarrow {C_{\Delta MAB}} = 2\sqrt {11}  + 2\sqrt {29}  \Rightarrow {p_{\Delta MAB}} = \sqrt {11}  + \sqrt {29}  \Rightarrow \left\{ \begin{array}{l}a = 11\\b = 29\end{array} \right. \Rightarrow a + b = 40\).