Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho hình hộp $ABCD.A'B'C'D'$ biết $A\left( {1;0;1} \right),\,\,B\left( {2;1;2} \right),\,\,D\left( {2; - 2;2} \right)$,$A'(3;0; - 1)$, điểm M thuộc cạnh DC . GTNN của tổng các khoảng cách $AM + MC'$ là:
Trả lời bởi giáo viên
Đáp án đúng: c
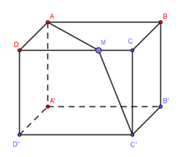
$AB = \sqrt 3 ,\,\,AD = \sqrt 6 ,\,\,AA' = 2\sqrt 2 $
Gọi độ dài đoạn $DM = x,\,\,\left( {0 \le x \le \sqrt 3 } \right)$. Khi đó, tổng các khoảng cách:
$AM + MC' = \sqrt {6 + {x^2}} + \sqrt {8 + {{\left( {\sqrt 3 - x} \right)}^2}} \ge \sqrt {{{\left( {\sqrt 6 + \sqrt 8 } \right)}^2} + {{\left( {x + \sqrt 3 - x} \right)}^2}} = \sqrt {6 + 8\sqrt 3 + 8 + 3} = \sqrt {17 + 8\sqrt 3 } $
$ \Rightarrow AM + MC'\,\,\min = \sqrt {17 + 8\sqrt 3 } $ khi và chỉ khi $\dfrac{{\sqrt 6 }}{{\sqrt 8 }} = \dfrac{x}{{\sqrt 3 - x}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow 2x = 3 - \sqrt 3 x \Leftrightarrow x = \dfrac{3}{{2 + \sqrt 3 }} = 6 - 3\sqrt 3 $.
Hướng dẫn giải:
Đánh giá theo bất đẳng thức: $\sqrt {{a^2} + {b^2}} + \sqrt {{c^2} + {d^2}} \ge \sqrt {{{(a + c)}^2} + {{(b + d)}^2}} $
Dấu “=” xảy ra khi và chỉ khi $\dfrac{a}{c} = \dfrac{b}{d}$.
