Ứng dụng tích phân trong hình học (diện tích hình phẳng)

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), đường thẳng \(y = 0\) và hai đường thẳng \(x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x =  - 1;x =  - 3\) là: \(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} - 1} \right|dx} \)

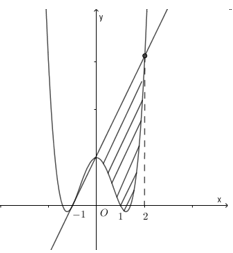
Đồ thị hàm số đi qua điểm \(\left( -1;0 \right);\left( 1;0 \right)\) nên ta có:

\(y=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-m \right)={{x}^{4}}-\left( 1+m \right){{x}^{2}}+m\,\,\left( m>1 \right)\)

\(y'=4{{x}^{3}}-2\left( 1+m \right)x=2x\left( 2{{x}^{2}}-1-m \right)\)

\(y'\left( -1 \right)=-2\left( 1-m \right)=2m-2\)

Phương trình tiếp tuyến tại \(A\left( -1;0 \right)\) có phương trình \(y=\left( 2m-2 \right)\left( x+1 \right)\)

\(\begin{align} & \int\limits_{0}^{2}{\left( \left( 2m-2 \right)\left( x+1 \right)-\left( {{x}^{4}}-\left( 1+m \right){{x}^{2}}+m \right) \right]}dx=\frac{28}{5} \\ & \Leftrightarrow \left( 2m-2 \right)\left. \left( \frac{{{x}^{2}}}{2}+x \right) \right|_{0}^{2}-\left. \left( \frac{{{x}^{5}}}{5}-\left( 1+x \right)\frac{{{x}^{3}}}{3}+mx \right) \right|_{0}^{2}=\frac{28}{5} \\ & \Leftrightarrow 4\left( 2m-2 \right)+\frac{8}{5}-2m=\frac{28}{5} \\ & \Leftrightarrow 6m=12 \\ & \Leftrightarrow m=2 \\ \end{align}\)

Khi đó hàm số (C) có dạng: \(y=\left( {{x}^{2}}-2 \right)\left( {{x}^{2}}-1 \right)={{x}^{4}}-3{{x}^{2}}+2\)

Phương trình tiếp tuyến tại A có dạng: \(y=2x+2\)

\(S=\int\limits_{-1}^{0}{\left( {{x}^{4}}-3{{x}^{2}}+2-2x-2 \right)dx=\int\limits_{-1}^{0}{\left( {{x}^{4}}-3{{x}^{2}}-2x \right)dx}=\frac{1}{5}}\)

Ta dễ dàng tìm được phương trình parabol là \(y={{x}^{2}}-4x+3\)

Xét phương trình hoành độ giao điểm \({{x}^{2}}-4x+3=0\Leftrightarrow \left[ \begin{align}x=1 \\x=3 \\\end{align} \right.\)

Khi đó diện tích giới hạn bởi \(\left( P \right)\) và trục hoành là \(S=-\int\limits_{1}^{3}{\left( {{x}^{2}}-4x+3 \right)dx}=\frac{4}{3}\)

Xét phương trình hoành độ giao điểm \({{x}^{2}}-2x=-{{x}^{2}}+4x\Leftrightarrow 2{{x}^{2}}=6x\Leftrightarrow \left[ \begin{align}  x=0 \\  x=3 \\ \end{align} \right.\)

\(\Rightarrow S=\int\limits_{0}^{3}{\left| {{x}^{2}}-2x+{{x}^{2}}-4x \right|dx}=9\)

Xét phương trình hoành độ giao điểm: \({{x}^{2}}-4x+4=0\Leftrightarrow x=2\)

\(\Rightarrow \) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y={{x}^{2}}-4x+4\), trục tung và trục hoành là \(S=\int\limits_{0}^{2}{\left| {{x}^{2}}-4x+4 \right|dx}=\frac{8}{3}\)

Đường thẳng (d) đi qua A(0;4) và có hệ số góc là k chia hình (H) thành hai phần:

Phần 1: Tam giác vuông OAB có diện tích S₁.

Phần 2: Hình phẳng giới hạn bởi đường thẳng (d), đồ thị hàm số \(y={{x}^{2}}-4x+4\) và trục hoành.

Đường thẳng (d) có phương trình \(y=kx+4\) cắt trục hoành tại điểm \(B\left( -\frac{4}{k};0 \right)\), với \({{x}_{B}}\in \left[ 0;2 \right]\Rightarrow k\le -2\) 

Đường thẳng (d) chia (H) thành hai phần có diện tích bằng nhau\(\Rightarrow {{S}_{1}}=\frac{1}{2}OA.OB=\frac{1}{2}.4.\left| \frac{-4}{k} \right|=\frac{4}{3}\)

\(\Rightarrow \left| \frac{1}{k} \right|=\frac{1}{6}\Leftrightarrow k=\pm 6\Rightarrow k=-6\)

Xét phương trình hoành độ giao điểm \({x^3} = 0 \Leftrightarrow x = 0 \notin \left[ {1;3} \right]\)

\(S = \int\limits_1^3 {\left| {{x^3}} \right|dx}  = \left| {\int\limits_1^3 {{x^3}dx} } \right| = 20\).

Phương trình hoành độ giao điểm của \(\left( {{P}_{1}} \right)\) và \(\left( {{P}_{2}} \right)\) là \(-\,{{x}^{2}}+2x+1=2{{x}^{2}}-4x+1\Leftrightarrow \left[ \begin{align} x=0 \\  x=2 \\ \end{align} \right..\)

Khi đó, diện tích hình phẳng cần tính là \(S=\int\limits_{0}^{2}{\left| -\,{{x}^{2}}+2x+1-2{{x}^{2}}+4x-1 \right|\,\text{d}x}=3\,\int\limits_{0}^{2}{\left| {{x}^{2}}-2x \right|\,\text{d}x}\)

\(=3\,\left| \int\limits_{0}^{2}{\left( {{x}^{2}}-2x \right)\,\text{d}x} \right|=3\,\left| \left. \left( \frac{{{x}^{3}}}{3}-{{x}^{2}} \right) \right|_{0}^{2} \right|=3\left| \frac{{{2}^{3}}}{3}-{{2}^{2}} \right|=3.\frac{4}{3}=4.\)

Vậy diện tích \(S=4.\)

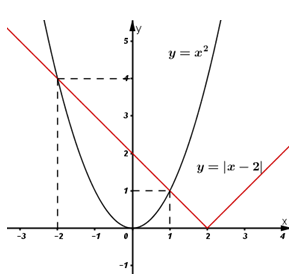
Hoành độ giao điểm của \(\left( C \right)\) và \(\left( d \right)\) là nghiệm phương trình: \({{x}^{2}}=\left| x-2 \right|\)

\(\begin{array}{l}
\Leftrightarrow {x^4} = {x^2} - 4x + 4 \Leftrightarrow {x^4} - {x^2} + 4x - 4 = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + {x^2} + 4} \right) = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right)\left( {{x^2} - x + 2} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x - 1 = 0\\
x + 2 = 0\\
{x^2} - x + 2 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - \,2\\
x = 1
\end{array} \right..
\end{array}\)

Diện tích hình phẳng cần tính là :

\(\begin{align}  & S=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}-\left| x-2 \right| \right|\,\text{d}x}=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}-\left( -x+2 \right) \right|\,\text{d}x}=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}+x-2 \right|\,\text{d}x} \\& =\int\limits_{-\,2}^{1}{\left( -{{x}^{2}}-x+2 \right)\,\text{d}x}=\left. \left( -\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+2x \right) \right|_{-2}^{1}=\frac{9}{2}. \\\end{align}\)

Diện tích hình phẳng giới hạn bởi đồ thị hàm số (C) và trục hoành là:

\(S=\int\limits_{-1}^{4}{\left| {{x}^{3}}-3{{x}^{2}}-4x \right|dx}=\int\limits_{-1}^{0}{\left| {{x}^{3}}-3{{x}^{2}}-4x \right|dx+}\int\limits_{0}^{4}{\left| {{x}^{3}}-3{{x}^{2}}-4x \right|dx}=\int\limits_{-1}^{0}{\left( {{x}^{3}}-3{{x}^{2}}-4x \right)dx-}\int\limits_{0}^{4}{\left( {{x}^{3}}-3{{x}^{2}}-4x \right)dx}\)

Hoành độ giao điểm của parabol \(y = {x^2} - 1\) và đường thẳng \(y = 3\) là nghiệm của phương trình:

\({x^2} - 1 = 3 \Leftrightarrow x =  \pm 2\)

Diện tích hình phẳng cần tìm là \(\int\limits_{ - 2}^2 {\left| {{x^2} - 4} \right|dx}  = \dfrac{{32}}{3}\)

Hoành độ giao điểm của \(\left( {{P}_{1}} \right),\,\,\left( {{P}_{2}} \right)\) là nghiệm của phương trình: \({{x}^{2}}-2x=-\,{{x}^{2}}+x\Leftrightarrow \left[ \begin{align}  x=0 \\  x=\frac{3}{2} \\ \end{align} \right..\)

Vậy diện tích cần tính là \(S=\int\limits_{0}^{\frac{3}{2}}{\left| {{x}^{2}}-2x-\left( -\,{{x}^{2}}+x \right) \right|\,\text{d}x}=\int\limits_{0}^{\frac{3}{2}}{\left| 2{{x}^{2}}-3x \right|\,\text{d}x}=\int\limits_{0}^{\frac{3}{2}}{\left( 3x-2{{x}^{2}} \right)\,\text{d}x}=\frac{9}{8}.\)

Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm phương trình: \({{x}^{2}}-2x=x\Leftrightarrow \left[ \begin{align}  & x=0 \\  & x=3 \\ \end{align} \right..\)

Vậy diện tích hình phẳng cần tính là \(S=\int\limits_{0}^{3}{\left| {{x}^{2}}-3x \right|\,\text{d}x}=\int\limits_{0}^{3}{\left( 3x-{{x}^{2}} \right)\,\text{d}x}=\left. \left( \frac{3{{x}^{2}}}{2}-\frac{{{x}^{3}}}{3} \right) \right|_{0}^{3}=\frac{9}{2}.\)

Xét phương trình hoành độ giao điểm \({x^3} - x = x - {x^2} \Leftrightarrow {x^3} + {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 2\end{array} \right.\).

Diện tích hình phẳng giới hạn bởi hai đường cong \(y = {x^3} - x\) và \(y = x - {x^2}\) là:

\(S = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right| + \left| {\int\limits_0^1 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right| = \frac{8}{3} + \frac{5}{{12}} = \frac{{37}}{{12}}\)

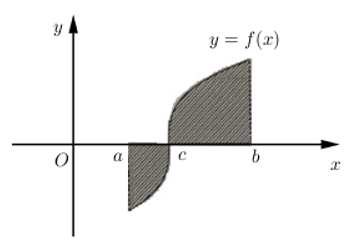
\(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}=\int\limits_{a}^{c}{\left| f\left( x \right) \right|dx}+\int\limits_{c}^{b}{\left| f\left( x \right) \right|dx}=-\int\limits_{a}^{c}{f\left( x \right)dx}+\int\limits_{c}^{b}{f\left( x \right)dx}\)

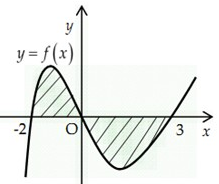
Ta có \(S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx}  = \int\limits_{ - 2}^0 {f\left( x \right)dx}  - \int\limits_0^3 {f\left( x \right)dx}  = \int\limits_{ - 2}^0 {f\left( x \right)dx}  + \int\limits_3^0 {f\left( x \right)dx} \)

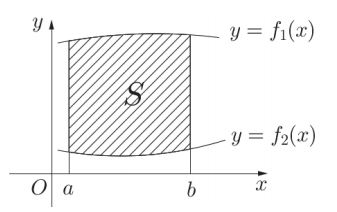
Diện tích hình phẳng giới hạn bởi \(y = {f_1}\left( x \right),y = {f_2}\left( x \right),x = a,x = b\) là: \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)

Ta thấy \({f_1}\left( x \right) > {f_2}\left( x \right)\,\,\forall x \in \left( {a;b} \right) \Rightarrow S = \int\limits_a^b {\left( {{f_1}\left( x \right) - {f_2}\left( x \right)} \right)dx} \)

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = x{e^x}\) , trục hoành, hai đường thẳng \(x =  - 2;x = 3\) có công thức tính là \(S = \int\limits_{ - 2}^3 {\left| {x{e^x}} \right|dx} .\)

Cách 1:

Bước 1: Tách thành tích phân trên các đoạn [-1;2]; [2;4]

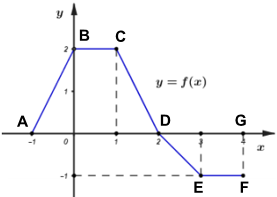
Gọi A, B, C, D, E, F, G lần lượt là các điểm như hình vẽ.

Xét \(I = \int\limits_{ - 1}^4 {f\left( x \right)dx} \) \( = \int\limits_{ - 1}^2 {f\left( x \right)dx}  + \int\limits_2^4 {f\left( x \right)dx} \)

\( = {S_{ABCD}} - {S_{DEFG}}\)

Bước 2: Sử dụng công thức tính diện tích hình thang để tính diện tích từng đoạn.

Ta có:

\({S_{ABCD}} = \dfrac{{OB.\left( {BC + AD} \right)}}{2} = \dfrac{{2.\left( {1 + 3} \right)}}{2} = 4\)

\({S_{DEFG}} = \dfrac{{FG\left( {EF + DG} \right)}}{2} = \dfrac{{1.\left( {1 + 2} \right)}}{2} = \dfrac{3}{2}\)

\( \Rightarrow I = 4 - \dfrac{3}{2} = \dfrac{5}{2}\)

Cách 2:

Từ hình vẽ ta thấy:

\(f\left( x \right) = \left\{ \begin{array}{l}2x + 2khi - 1 \le x \le 0\\2khi0 \le x \le 1\\ - 2x + 4khi1 \le x \le 2\\ - x + 2khi2 \le x \le 3\\ - 1khi3 \le x \le 4\end{array} \right.\)

\( \Rightarrow I = \int\limits_{ - 1}^4 {f\left( x \right)dx} \)

\( = \int\limits_{ - 1}^0 {f\left( x \right)dx}  + \int\limits_0^1 {f\left( x \right)dx}  + \int\limits_1^2 {f\left( x \right)dx} \)\( + \int\limits_2^3 {f\left( x \right)dx}  + \int\limits_3^4 {f\left( x \right)dx} \)

\( = \int\limits_{ - 1}^0 {\left( {2x + 2} \right)dx}  + \int\limits_0^1 {2dx}  + \int\limits_1^2 {\left( { - 2x + 4} \right)dx} \)\( + \int\limits_2^3 {\left( { - x + 2} \right)dx}  + \int\limits_3^4 {\left( { - 1} \right)dx} \)

\( = 1 + 2 + 1 - \dfrac{1}{2} - 1 = \dfrac{5}{2}\)

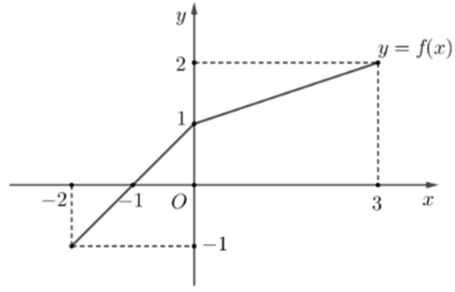
Bước 1: Tách thành tích phân trên các đoạn [-2;-1]; [-1;0]; [0;3]

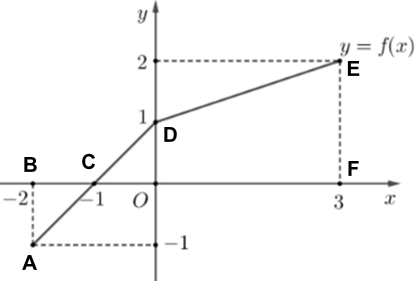
Gọi A, B, C, D, E, F lần lượt là các điểm như hình vẽ.

Xét \(I = \int\limits_{ - 2}^3 {f\left( x \right)dx} \) \( = \int\limits_{ - 2}^{ - 1} {f\left( x \right)dx}  + \int\limits_{ - 1}^0 {f\left( x \right)dx}  + \int\limits_0^3 {f\left( x \right)dx} \)

\( =  - {S_{ABC}} + {S_{OCD}} + {S_{ODEF}}\)

Bước 2: Sử dụng công thức tính diện tích tam giác và hình thang đề tính diện tích từng đoạn.

Ta có

\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.AB.BC = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\\{S_{OCD}} = \dfrac{1}{2}.OC.OD = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\\{S_{ODEF}} = \dfrac{{OF\left( {OD + EF} \right)}}{2} = \dfrac{9}{2}\end{array}\)

\( \Rightarrow I =  - \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{9}{2}\)\( = \dfrac{9}{2}\)