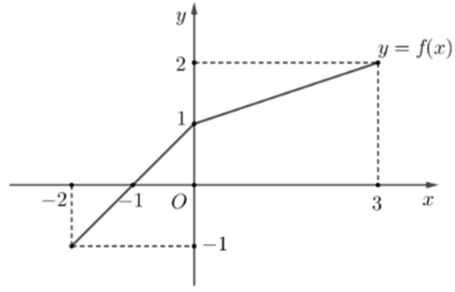
Cho hàm số \(f\left( x \right)\) có đồ thị như hình vẽ. Tính tích phân \(\int\limits_{ - 2}^3 {f\left( x \right)dx} \)
Trả lời bởi giáo viên
Bước 1: Tách thành tích phân trên các đoạn [-2;-1]; [-1;0]; [0;3]
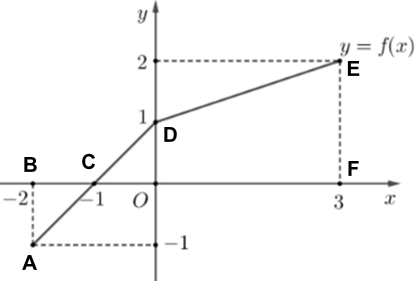
Gọi A, B, C, D, E, F lần lượt là các điểm như hình vẽ.
Xét \(I = \int\limits_{ - 2}^3 {f\left( x \right)dx} \) \( = \int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} + \int\limits_{ - 1}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \)
\( = - {S_{ABC}} + {S_{OCD}} + {S_{ODEF}}\)
Bước 2: Sử dụng công thức tính diện tích tam giác và hình thang đề tính diện tích từng đoạn.
Ta có
\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.AB.BC = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\\{S_{OCD}} = \dfrac{1}{2}.OC.OD = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\\{S_{ODEF}} = \dfrac{{OF\left( {OD + EF} \right)}}{2} = \dfrac{9}{2}\end{array}\)
\( \Rightarrow I = - \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{9}{2}\)\( = \dfrac{9}{2}\)
Hướng dẫn giải:
Bước 1: Tách thành tích phân trên các đoạn [-2;-1]; [-1;0]; [0;3]
Bước 2: Sử dụng công thức tính diện tích tam giác và hình thang đề tính diện tích từng đoạn.