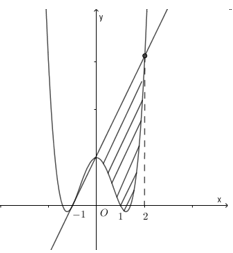
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) ($a=1$) có đồ thị (C), biết rằng (C) đi qua \(A\left( -1;0 \right)\) , tiếp tuyến d tại A của (C) và hai đường thẳng \(x=0;x=2\) có diện tích bằng \(\dfrac{28}{5}\) (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng \(x=-1;x=0\) có diện tích bằng

Đồ thị hàm số đi qua điểm \(\left( -1;0 \right);\left( 1;0 \right)\) nên ta có:

\(y=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-m \right)={{x}^{4}}-\left( 1+m \right){{x}^{2}}+m\,\,\left( m>1 \right)\)

\(y'=4{{x}^{3}}-2\left( 1+m \right)x=2x\left( 2{{x}^{2}}-1-m \right)\)

\(y'\left( -1 \right)=-2\left( 1-m \right)=2m-2\)

Phương trình tiếp tuyến tại \(A\left( -1;0 \right)\) có phương trình \(y=\left( 2m-2 \right)\left( x+1 \right)\)

\(\begin{align} & \int\limits_{0}^{2}{\left( \left( 2m-2 \right)\left( x+1 \right)-\left( {{x}^{4}}-\left( 1+m \right){{x}^{2}}+m \right) \right]}dx=\frac{28}{5} \\ & \Leftrightarrow \left( 2m-2 \right)\left. \left( \frac{{{x}^{2}}}{2}+x \right) \right|_{0}^{2}-\left. \left( \frac{{{x}^{5}}}{5}-\left( 1+x \right)\frac{{{x}^{3}}}{3}+mx \right) \right|_{0}^{2}=\frac{28}{5} \\ & \Leftrightarrow 4\left( 2m-2 \right)+\frac{8}{5}-2m=\frac{28}{5} \\ & \Leftrightarrow 6m=12 \\ & \Leftrightarrow m=2 \\ \end{align}\)

Khi đó hàm số (C) có dạng: \(y=\left( {{x}^{2}}-2 \right)\left( {{x}^{2}}-1 \right)={{x}^{4}}-3{{x}^{2}}+2\)

Phương trình tiếp tuyến tại A có dạng: \(y=2x+2\)

\(S=\int\limits_{-1}^{0}{\left( {{x}^{4}}-3{{x}^{2}}+2-2x-2 \right)dx=\int\limits_{-1}^{0}{\left( {{x}^{4}}-3{{x}^{2}}-2x \right)dx}=\frac{1}{5}}\)