Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\,y = 0,x = - 2\) và \(x = 3\) (như hình vẽ bên).
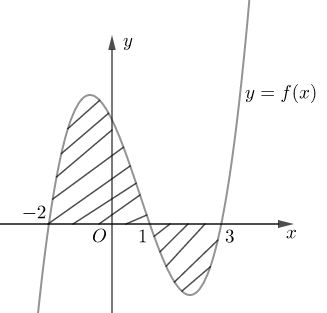
Mệnh đề nào dưới đây đúng?
Diện tích phần gạch chéo là:
\(S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} \)
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn [0;5] là đường gấp khúc như hình vẽ. Tính tích phân \(\int\limits_0^5 {\left[ {2f\left( x \right) - 1} \right]dx} \)
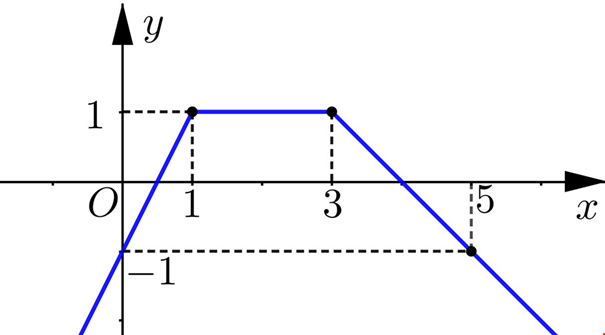
Bước 1: Tách \(I = \int\limits_0^5 {f\left( x \right)dx} \) thành tích phân trên các đoạn \(\left[ {0;\dfrac{1}{2}} \right];\left[ {\dfrac{1}{2};4} \right];\left[ {4;5} \right]\)
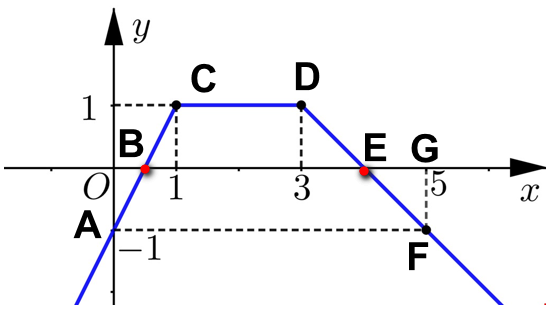
Gọi A, B, C, D, E, F,G lần lượt là các điểm như hình vẽ.
Xét \(I = \int\limits_0^5 {f\left( x \right)dx} \) \( = \int\limits_0^{\dfrac{1}{2}} {f\left( x \right)dx} + \int\limits_{\dfrac{1}{2}}^4 {f\left( x \right)dx} + \int\limits_4^5 {f\left( x \right)dx} \)
\( = - {S_{OAB}} + {S_{BCDE}} - {S_{EFG}}\)
Bước 2: Sử dụng công thức tính diện tích tam giác và hình thang đề tính diện tích từng đoạn rồi tính tích phân cần tìm.
Ta có
\(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}.OA.OB = \dfrac{1}{2}.1.\dfrac{1}{2} = \dfrac{1}{4}\\{S_{BCDE}} = \dfrac{1}{2}.1.\left( {2 + \dfrac{7}{2}} \right) = \dfrac{{11}}{4}\\{S_{EFG}} = \dfrac{1}{2}.EG.FG = \dfrac{1}{2}\end{array}\)
\(\begin{array}{l} \Rightarrow I = - \dfrac{1}{4} + \dfrac{{11}}{4} - \dfrac{1}{2} = 2\\ \Rightarrow \int\limits_0^5 {\left[ {2f\left( x \right) - 1} \right]dx} = 2\int\limits_0^5 {f\left( x \right)dx} - 5\\ = 2I - 5 = - 1\end{array}\)
Đề thi THPT QG 2019 – mã đề 104
Cho đường thẳng \(y = \dfrac{3}{2}x\) và parabol \(y = {x^2} + a\) (\(a\) là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.
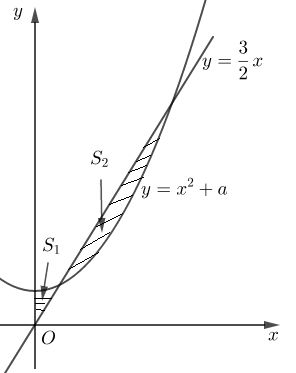
Khi \({S_1} = {S_2}\) thì \(a\) thuộc khoảng nào dưới đây ?
Xét phương trình hoành độ giao điểm \({x^2} + a = \dfrac{3}{2}x \Leftrightarrow 2{x^2} - 3x + 2a = 0\,\,\left( * \right)\).
Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \Delta = 9 - 8a > 0 \Leftrightarrow a < \dfrac{9}{8}\).
Kết hợp điều kiện đề bài \( \Rightarrow 0 < a < \dfrac{9}{8}\).
Gọi \({x_1},\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) là 2 nghiệm của phương trình (*). Khi đó ta có:
\(\begin{array}{l}{S_1} = \int\limits_0^{{x_1}} {\left( {{x^2} + a - \dfrac{3}{2}x} \right)dx} = \left. {\left( {\dfrac{{{x^3}}}{3} + ax - \dfrac{{3{x^2}}}{4}} \right)} \right|_0^{{x_1}} = \dfrac{{x_1^3}}{3} + a{x_1} - \dfrac{{3x_1^2}}{4}\\{S_2} = \int\limits_{{x_1}}^{{x_2}} {\left( {\dfrac{3}{2}x - {x^2} - a} \right)dx} = \left. {\left( {\dfrac{{3{x^2}}}{4} - \dfrac{{{x^3}}}{3} - ax} \right)} \right|_{{x_1}}^{{x_2}} = \left( {\dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2}} \right) - \left( {\dfrac{{3x_1^2}}{4} - \dfrac{{x_1^3}}{3} - a{x_1}} \right)\end{array}\)
Theo bài ra ta có: \({S_1} = {S_2}\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{x_1^3}}{3} + a{x_1} - \dfrac{{3x_1^2}}{4} = \left( {\dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2}} \right) - \left( {\dfrac{{3x_1^2}}{4} - \dfrac{{x_1^3}}{3} - a{x_1}} \right)\\ \Leftrightarrow \dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2} = 0 \Leftrightarrow 9x_2^2 - 4x_2^3 - 12a{x_2} = 0\\ \Leftrightarrow {x_2}\left( {4x_2^2 - 9{x_2} + 12a} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} = 0\\4x_2^2 - 9{x_2} + 12a = 0\end{array} \right.\end{array}\)
TH1: \({x_2} = 0 \Rightarrow \) Thay vào (*) ta có \(2a = 0 \Leftrightarrow a = 0\,\,\left( {ktm} \right)\).
TH2: \(4x_2^2 - 9{x_2} + 12a = 0\) (1).
Vì \({x_2}\) là nghiệm của (*) nên \(2x_2^2 - 3{x_2} + 2a = 0 \Leftrightarrow 12x_2^2 - 18{x_2} + 12a = 0\) (2).
Trừ vế theo vế của (2) cho (1) ta được \(8x_2^2 - 9{x_2} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} = 0\\{x_2} = \dfrac{9}{8}\end{array} \right.\).
Với \({x_2} = 0 \Leftrightarrow 2a = 0 \Leftrightarrow a = 0\,\,\left( {ktm} \right)\).
Với \({x_2} = \dfrac{9}{8} \Leftrightarrow 2.{\left( {\dfrac{9}{8}} \right)^2} - 3.\dfrac{9}{8} + 2a = 0 \Leftrightarrow a = \dfrac{{27}}{{64}}\,\,\left( {tm} \right) = 0,421875\).
Vậy \(a \in \left( {\dfrac{2}{5};\dfrac{9}{{20}}} \right).\)
Cho hàm số \(f(x) = 3{x^4} + a{x^3} + b{x^2} + cx + d(a,b,c,d \in \mathbb{R})\) có ba điểm cực trị là \( - 2\), \( - 1\) và 1. Gọi \(y = g(x)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f(x)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f(x)\) và \(y = g(x)\) bằng
Ta có: \({f^\prime }(x) = 12{x^3} + 3a{x^2} + 2bx + c\)
Theo bài ra, ta có: \(\left\{ {\begin{array}{*{20}{l}}{12a - 4b + c = 96}\\{3a - 2b + c = 12}\\{3a + 2b + c = - 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 8}\\{b = - 6}\\{c = - 24}\end{array}} \right.} \right.\)
\( \Rightarrow f(x) = 3{x^4} + 8{x^3} - 6{x^2} - 24x + d\)
Giả sử \(y = g(x) = a{x^2} + bx + c\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{g( - 2) = 8 + d}\\{g( - 1) = 13 + d}\\{g(1) = - 19 + d}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4a - 2b + c = 8 + d}\\{a - b + c = 13 + d}\\{a + b + c = - 19 + d}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 7}\\{b = - 16}\\{c = 4 + d}\end{array}} \right.} \right.\)
\( \Rightarrow y = g(x) = - 7{x^2} - 16x + 4 + d\)
Ta có:\(f(x) - g(x) = 0\)
\( \Leftrightarrow 3{x^4} + 8{x^3} + {x^2} - 8x - 4 = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - \dfrac{2}{3}}\\{x = - 1}\\{x = - 2}\end{array}} \right.\)
Diện tích hình phẳng cần tìm:
\(S = \int_{ - 2}^1 | f(x) - g(x)|dx\) \( = \int_{ - 2}^1 {\left| {3{x^4} + 8{x^3} + {x^2} - 8x - 4} \right|} dx\)
\( = \int_{ - 2}^{ - 1} {\left| {3{x^4} + 8{x^3} + {x^2} - 8x - 4} \right|} dx\) \( + \int_{ - 1}^{ - \dfrac{2}{3}} {\left| {3{x^4} + 8{x^3} + {x^2} - 8x - 4} \right|} dx\) \( + \int_{ - \dfrac{2}{3}}^1 {\left| {3{x^4} + 8{x^3} + {x^2} - 8x - 4} \right|} dx\)
\( = \dfrac{{2948}}{{405}}\)
Kết luận: \(S = \dfrac{{2948}}{{405}}\)
Cho hàm số \(y=f(x)\) liên tục trên \(\left[ a;b \right]\). Diện tích hình phẳng $(H)$ giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a;\,\,x=b\) được tính theo công thức
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a;\,\,x=b\) được tính theo công thức : \(S=\int\limits_{a}^{b}{\left| f(x) \right|dx}\)
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là \(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\).
Hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ 1;\ 3 \right]\) , trục $Ox$ và hai đường thẳng \(x=1,\ \ x=3\) có diện tích là:
Áp dụng công thức tính diện tích hình phẳng ta được: \(S=\int\limits_{1}^{3}{\left| f\left( x \right) \right|dx.}\)
Cho hàm số \(y=f\left( x \right),\,\,y=g\left( x \right)\) liên tục trên \(\left[ a;b \right].\) Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi hai đồ thị \(y=f\left( x \right),\,\,y=g\left( x \right)\) và các đường thẳng \(x=a,\,\,x=b.\) Diện tích \(\left( H \right)\) được tính theo công thức
Diện tích hình phẳng \(\left( H \right)\) cần tính là \({{S}_{H}}=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|\text{d}x}.\)
Cho hai hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right].\) Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng \(x=a,\,\,x=b\,\,\,\left( a < b \right).\) Diện tích \(S\) của hình phẳng \(D\) được tính bởi công thức:
Diện tích \(S\) của hình phẳng \(D\) được tính theo công thức là \(S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|\,\text{d}x}.\)
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,\,\,b,\,\,c\) là các số thực. Biết hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\) có hai giá trị cực trị là \( - 5\) và \(3\). Diện tích hình phẳng giới hạn bởi các đường \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}\) và \(y = 1\) bằng:
* Xét phương trình hoành độ giao điểm:
\(\dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}} = 1 \Leftrightarrow f\left( x \right) = g\left( x \right) + 6 \Leftrightarrow f\left( x \right) - g\left( x \right) - 6 = 0\).
(Chúng ta không cần lo điều kiện \(g\left( x \right) + 6 \ne 0\), bởi lẽ đồ thị hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}\) khi tương giao với đường thẳng \(y = 1\) phải tạo nên một miền kín, và khi số nghiệm của phương trình \(f\left( x \right) = g\left( x \right) + 6\) nhiều hơn 2 thì ta mới phải chú ý xem xét lấy cận từ đâu đến đâu, và liệu rằng có phải từ \({x_{\min }} \to {x_{\max }}\), chẳng may đồ thị tương giao bị gián đoạn trên đoạn \(\left[ {{x_{\min }};{x_{\max }}} \right]\) mà vẫn tạo miền kín. Trên thực tế, bài toán này phương trình \(f\left( x \right) = g\left( x \right) + 6\) chỉ có 2 nghiệm (vì là phương trình bậc hai), nên người giải toán không cần quan tâm đến việc gián đoạn hay không, vì việc tồn tại nghiệm hình và hàm số là thuộc phạm trù người ra đề).
Mà \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\) \( \Rightarrow f\left( x \right) - g\left( x \right) = - f'\left( x \right) - f''\left( x \right)\)
\( \Rightarrow \) Phương trình hoành độ giao điểm trở thành:
\( - f'\left( x \right) - f''\left( x \right) - 6 = 0 \Leftrightarrow f'\left( x \right) + f''\left( x \right) + 6 = 0\) (1)
Mặt khác: \(g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + f'''\left( x \right)\) và \(f'''\left( x \right) = 6\) \( \Rightarrow g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + 6\).
Từ phương trình (1) \( \Leftrightarrow g'\left( x \right) = 0\).
Theo giả thiết \(g\left( x \right)\) có 2 điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(\left\{ \begin{array}{l}g\left( {{x_1}} \right) = - 5\\g\left( {{x_2}} \right) = 3\end{array} \right.\) \( \Rightarrow g'\left( x \right) = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\).
Vậy phương trình hoành độ giao điểm có 2 nghiệm \({x_1},\,\,{x_2}\).
\(\begin{array}{l} \Rightarrow {S_{\left( H \right)}} = \left| {\int\limits_{{x_1}}^{{x_2}} {\left( {\dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}} - 1} \right)dx} } \right| = \left| {\int\limits_{{x_1}}^{{x_2}} {\dfrac{{f\left( x \right) - g\left( x \right) - 6}}{{g\left( x \right) + 6}}dx} } \right|\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {\int\limits_{{x_1}}^{{x_2}} {\dfrac{{ - f'\left( x \right) - f''\left( x \right) - 6}}{{g\left( x \right) + 6}}dx} } \right| = \left| {\int\limits_{{x_1}}^{{x_2}} {\dfrac{{ - g'\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right|\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {\int\limits_{{x_1}}^{{x_2}} {\dfrac{{g'\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right| = \left| {\int\limits_{{x_1}}^{{x_2}} {\dfrac{{d\left( {g\left( x \right) + 6} \right)}}{{g\left( x \right) + 6}}} } \right| = \left| {\ln \left. {\left| {g\left( x \right) + 6} \right|} \right|_{{x_1}}^{{x_2}}} \right|\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {\ln \left| {g\left( {{x_2}} \right) + 6} \right| - \ln \left| {g\left( {{x_1}} \right) + 6} \right|} \right| = \left| {\ln \left| {3 + 6} \right| - \ln \left| { - 5 + 6} \right|} \right| = \ln 9 - \ln 1 = 2\ln 3\end{array}\)
Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x=0,\,\,x=\pi ,\) đồ thị hàm số \(y=\cos x\) và trục \(Ox\) là
Diện tích hình phẳng cần tính là \(S=\int\limits_{0}^{\pi }{\left| \cos x \right|\,\text{d}x}.\)
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) là:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây ?
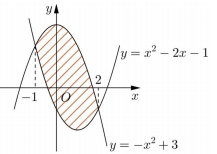
Dựa vào hình vẽ (ta thấy \(f\left( x \right)\) nằm trên \(g\left( x \right)\;\forall x \in \left[ { - 1;\;2} \right] \Rightarrow f\left( x \right) \ge g\left( x \right)\;\forall x \in \left[ { - 1;\;2} \right]\)) và công thức tính diện tích hình phẳng ta được công thức tính diện tích phân phần gạch chéo là:
\(S = \int\limits_{ - 1}^2 {\left( { - {x^2} + 3 - {x^2} + 2x + 1} \right)dx} = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} .\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn \(\left[ {0;3} \right]\) như hình vẽ
Tính tích phân \(I = \int\limits_0^3 {\left[ {2f\left( x \right) + 1} \right]dx} \) bằng
Ta có: \(I = \int\limits_0^3 {\left[ {2f\left( x \right) + 1} \right]dx} \) \( = \int\limits_0^3 {2f\left( x \right)dx} + \int\limits_0^3 {dx} \) \( = 2\int\limits_0^3 {f\left( x \right)dx} + 3\)
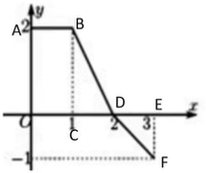
\(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^1 {f\left( x \right)dx} \) \( + \int\limits_1^2 {f\left( x \right)dx} + \int\limits_2^3 {f\left( x \right)dx} \)
\(\begin{array}{l} = {S_{OABC}} + {S_{BCD}} - {S_{DEF}}\\ = 2 + 1 - \dfrac{1}{2} = \dfrac{5}{2}\\ = > I = 2.\dfrac{5}{2} + 3 = 8\end{array}\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
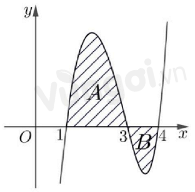
Biết các miền \(A\) và \(B\) có diện tích lần lượt là 5 và 2. Tính \(\int\limits_1^2 {6xf\left( {{x^2}} \right)dx} \).
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
Ta đặt \(I = \int\limits_1^2 {6xf\left( {{x^2}} \right)dx} \).
Đặt \(t = {x^2}\).
\( \Rightarrow dt = 2xdx\).
Khi đó \(I = \int\limits_1^4 {3f\left( t \right)dt} = 3\int\limits_1^4 {f\left( t \right)dt} \)
\( = 3\left[ {\int\limits_1^3 {f\left( t \right)dt + \int\limits_3^4 {f\left( t \right)dt} } } \right] = 3\left[ {\int\limits_1^3 {f\left( x \right)dx + \int\limits_3^4 {f\left( x \right)dx} } } \right]\)
\( = 3\left( {5 - 2} \right) = 9\).
Vậy \(\int\limits_1^2 {6xf\left( {{x^2}} \right)dx} = 9\).
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,b,c\) là các số thực. Biết hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\) có hai giá trị cực trị là \( - 5\) và \(2.\) Diện tích hình phẳng giới hạn bởi các đường \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}\) và \(y = 1\) bằng
Xét hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\)
Ta có: \(g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + f'''\left( x \right) = f'\left( x \right) + f''\left( x \right) + 6\)
Theo giả thiết ta có phương trình \(g'\left( x \right) = 0\) có hai nghiệm \(m,n\) và \(\left\{ \begin{array}{l}g\left( m \right) = - 5\\g\left( n \right) = 2\end{array} \right.\)
Xét phương trình \(\dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}} = 1 \Rightarrow g\left( x \right) + 6 - f\left( x \right) = 0 \Leftrightarrow f'\left( x \right) + f''\left( x \right) + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\x = n\end{array} \right.\)
Diện tích hình phẳng cần tính là:
\(\left| {\int\limits_m^n {\left( {1 - \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}} \right)dx} } \right| = \left| {\int\limits_m^n {\dfrac{{g\left( x \right) + 6 - f\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right| = \left| {\int\limits_m^n {\dfrac{{f'\left( x \right) + f''\left( x \right) + 6}}{{g\left( x \right) + 6}}dx} } \right|\) \( = \left| {\int\limits_m^n {\dfrac{{g'\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right|\)
\( = \left| {\ln \left| {g\left( x \right) + 6} \right|_m^n} \right| = \left| {\ln \left| {g\left( n \right) + 6} \right| - \ln \left| {g\left( m \right) + 6} \right|} \right| = \left| {\ln 8 - \ln 1} \right| = 3\ln 2.\)
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^3} - 4x\), trục hoành, đường thẳng \(x = - 2\) và đường thẳng \(x = 1\). Diện tích của hình phẳng \(\left( H \right)\) bằng
Ta có : \({x^3} - 4x = 0 \Leftrightarrow x\left( {{x^2} - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 2;1} \right]\\x = - 2 \in \left[ { - 2;1} \right]\\x = 2 \notin \left[ { - 2;1} \right]\end{array} \right.\).
\( \Rightarrow S = \int\limits_{ - 2}^1 {\left| {{x^3} - 4x} \right|dx} = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)dx} } \right| + \left| {\int\limits_0^1 {\left( {{x^3} - 4x} \right)dx} } \right| = 4 + \dfrac{7}{4} = \dfrac{{23}}{4}\).
Cho hình phẳng D được giới hạn bởi các đường \(x = 0,\,y = 2,\,y = x + 1\) và \(y = {x^2}\) như hình vẽ (phần màu vàng)
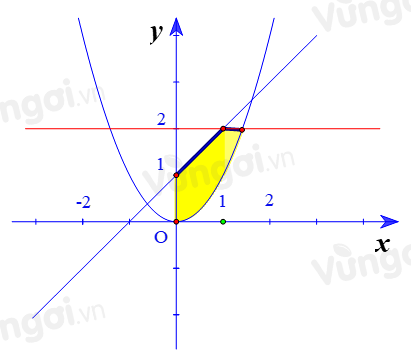
Diện tích của D là:
Bước 1: Tách hình tô đậm thành hiệu của hai hình: \({S_1} - {S_2}\)
Phần tô đậm của hình bằng \({S_1} - {S_2}\).
Trong đó \({S_1}\) là phần tạo bởi các đường \(x = 0;y = 2;y = {x^2}\). \({S_2}\) là phần tạo bởi các đường \(x = 0;y = 2;y = x + 1\).
Bước 2: Tính \({S_1};{S_2}\)
Hoành độ giao điểm bởi các đường \(x = 0;y = 2;y = {x^2}\) là:
\(\sqrt 2 ; - \sqrt 2 \)
Vì x>0 nên: \({S_1} = \int\limits_0^{\sqrt 2 } {\left| {2 - {x^2}} \right|dx} = \dfrac{{4\sqrt 2 }}{3}\)
\({S_2} = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\)
Bước 3: Tính \({S_1} - {S_2}\)
\({S_1} - {S_2} = - \dfrac{1}{2} + \dfrac{{4\sqrt 2 }}{3}\)
Một biển quảng cáo có dạng hình elip với bốn đỉnh \({A_1},\,\,{A_2},\,\,{B_1},\,\,{B_2}\) như hình vẽ bên. Biết chi phí để sơn phần tô đậm là 200.000 đồng/ m2 và phần còn lại là 100.000 đồng/m2. Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 8m,\,\,{B_1}{B_2} = 6m\) và tứ giác MNPQ là hình chữ nhật có \(MQ = 3m\) ?
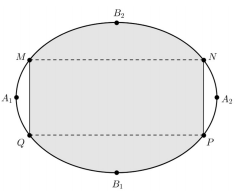
(E) đã cho có độ dài trục lớn \(2a = 8 \Rightarrow a = 4\), độ dài trục bé \(2b = 6 \Rightarrow b = 3\).
Ta có diện tích (E) bằng : \({S_{\left( E \right)}} = \pi .4.3 = 12\pi \,\,\left( {{m^2}} \right)\)
Phương trình \(\left( E \right):\,\,\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Rightarrow {y^2} = 9.\dfrac{{16 - {x^2}}}{{16}} \Leftrightarrow y = \pm \dfrac{{3\sqrt {16 - {x^2}} }}{4}\).
Ta có \(M \in \left( E \right);\,\,{y_M} = \dfrac{1}{2}MQ = \dfrac{3}{2} \Rightarrow {x_M} = - 2\sqrt 3 \Rightarrow M\left( { - 2\sqrt 3 ;\dfrac{3}{2}} \right)\)
Diện tích phần giới hạn bởi (E), trục Ox, đường thẳng MQ có diện tích:
\({S_{AMQ}} = 2\int\limits_{ - 4}^{ - 2\sqrt 3 } {\dfrac{{3\sqrt {16 - {x^2}} }}{4}dx} \approx 1,087 \Rightarrow \) Diện tích phần trắng là: \({S_{trang}} = 2{S_{AMQ}} = 2,174\,\,\left( {{m^2}} \right)\)
Khi đó diện tích phần xanh là \({S_{xanh}} = {S_{\left( E \right)}} - {S_{trang}} = 12\pi - 2,174 = 35,525\,\,\left( {{m^2}} \right)\).
Vậy chi phí để sơn biển quảng cáo là \(2,174.100 + 35,525.200 \approx 7322\) (nghìn đồng) \( \approx 7322000\) đồng.
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh \(A,B,C,D\) và hai đường parabol có các đỉnh lần lượt là \(E,F\) (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng \(AB\), đối xứng với nhau qua trục \(CD\), hai parabol cắt elip tại các điểm \(M,N,P,Q\). Biết \(AB = 8m,CD = 6m,MN = PQ = 3\sqrt 3 m,EF = 2m\). Chi phí để trồng hoa trên vườn là \(300.000\) đ/m2 . Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?
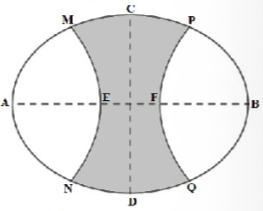
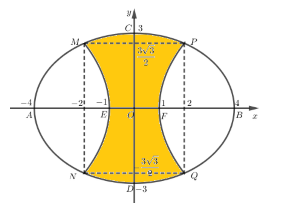
Gắn hệ trục tọa độ như hình vẽ, dễ thấy \(B\left( {4;0} \right),C\left( {0;3} \right),F\left( {1;0} \right)\).
Ta chỉ cần xét phần bên phải trục \(Oy\) vì hình vẽ có tính đối xứng.
Phương trình elip: \(\left( E \right):\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Rightarrow x = 4\sqrt {1 - \dfrac{{{y^2}}}{9}} \).
Dễ thấy \(PQ = 3\sqrt 3 \Rightarrow P\left( {m;\dfrac{{3\sqrt 3 }}{2}} \right)\) với \(m > 0\).
Mà \(P \in \left( E \right) \Rightarrow m = 4\sqrt {1 - \dfrac{{27/4}}{9}} = 2 \Rightarrow P\left( {2;\dfrac{{3\sqrt 3 }}{2}} \right)\).
Gọi phương trình parabol bên phải trục tung là \(\left( P \right):x = a{y^2} + by + c\).
Đỉnh \(F\left( {1;0} \right) \Rightarrow c = 1,b = 0 \Rightarrow x = a{y^2} + 1\)
\(P \in \left( P \right):x = a{y^2} + 1 \Leftrightarrow 2 = a.{\left( {\dfrac{{3\sqrt 3 }}{2}} \right)^2} + 1 \Leftrightarrow \dfrac{{27}}{4}a + 1 = 2 \Leftrightarrow a = \dfrac{4}{{27}}\) \( \Rightarrow \left( P \right):x = \dfrac{4}{{27}}{y^2} + 1\).
Diện tích hình phẳng giới hạn bởi elip \(\left( E \right)\) và parabol \(\left( P \right)\) (phần màu trắng) nên phải trục tung là:
\({S_1} = \int\limits_{ - \dfrac{{3\sqrt 3 }}{2}}^{\dfrac{{3\sqrt 3 }}{2}} {\left[ {4\sqrt {1 - \dfrac{{{y^2}}}{9}} - \dfrac{4}{{27}}{y^2} - 1} \right]dy} \)\( \Rightarrow 2{S_1} \approx 21,6686\)
Diện tích elip: \(S = \pi ab = \pi .4.3 = 12\pi \).
Diện tích phần tô màu đậm là \(S - 2{S_1} \approx 16,03\).
Số tiền trồng hoa là: \(16,03.300.000 = 4.809.000\)

