Câu hỏi:
2 năm trước
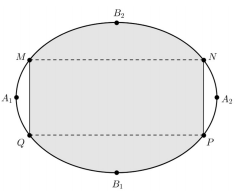
Một biển quảng cáo có dạng hình elip với bốn đỉnh \({A_1},\,\,{A_2},\,\,{B_1},\,\,{B_2}\) như hình vẽ bên. Biết chi phí để sơn phần tô đậm là 200.000 đồng/ m2 và phần còn lại là 100.000 đồng/m2. Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 8m,\,\,{B_1}{B_2} = 6m\) và tứ giác MNPQ là hình chữ nhật có \(MQ = 3m\) ?
Trả lời bởi giáo viên
Đáp án đúng: a
(E) đã cho có độ dài trục lớn \(2a = 8 \Rightarrow a = 4\), độ dài trục bé \(2b = 6 \Rightarrow b = 3\).
Ta có diện tích (E) bằng : \({S_{\left( E \right)}} = \pi .4.3 = 12\pi \,\,\left( {{m^2}} \right)\)
Phương trình \(\left( E \right):\,\,\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Rightarrow {y^2} = 9.\dfrac{{16 - {x^2}}}{{16}} \Leftrightarrow y = \pm \dfrac{{3\sqrt {16 - {x^2}} }}{4}\).
Ta có \(M \in \left( E \right);\,\,{y_M} = \dfrac{1}{2}MQ = \dfrac{3}{2} \Rightarrow {x_M} = - 2\sqrt 3 \Rightarrow M\left( { - 2\sqrt 3 ;\dfrac{3}{2}} \right)\)
Diện tích phần giới hạn bởi (E), trục Ox, đường thẳng MQ có diện tích:
\({S_{AMQ}} = 2\int\limits_{ - 4}^{ - 2\sqrt 3 } {\dfrac{{3\sqrt {16 - {x^2}} }}{4}dx} \approx 1,087 \Rightarrow \) Diện tích phần trắng là: \({S_{trang}} = 2{S_{AMQ}} = 2,174\,\,\left( {{m^2}} \right)\)
Khi đó diện tích phần xanh là \({S_{xanh}} = {S_{\left( E \right)}} - {S_{trang}} = 12\pi - 2,174 = 35,525\,\,\left( {{m^2}} \right)\).
Vậy chi phí để sơn biển quảng cáo là \(2,174.100 + 35,525.200 \approx 7322\) (nghìn đồng) \( \approx 7322000\) đồng.
Hướng dẫn giải:
+) Viết phương trình Elip, tính diện tích Elip.
+) Tính diện tích phần trắng, ứng dụng tích phân để tính diện tích hình phẳng.
+) Tính diện tích phần xanh sau đó tính chi phí để sơn.
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
