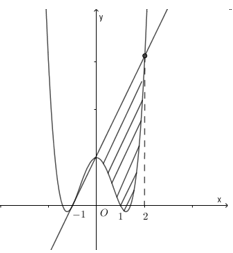
Cho hình phẳng D được giới hạn bởi các đường \(x = 0,\,y = 2,\,y = x + 1\) và \(y = {x^2}\) như hình vẽ (phần màu vàng)
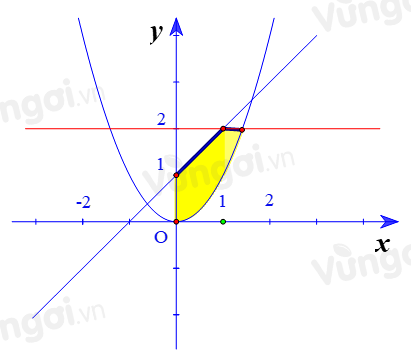
Diện tích của D là:
Trả lời bởi giáo viên
Bước 1: Tách hình tô đậm thành hiệu của hai hình: \({S_1} - {S_2}\)
Phần tô đậm của hình bằng \({S_1} - {S_2}\).
Trong đó \({S_1}\) là phần tạo bởi các đường \(x = 0;y = 2;y = {x^2}\). \({S_2}\) là phần tạo bởi các đường \(x = 0;y = 2;y = x + 1\).
Bước 2: Tính \({S_1};{S_2}\)
Hoành độ giao điểm bởi các đường \(x = 0;y = 2;y = {x^2}\) là:
\(\sqrt 2 ; - \sqrt 2 \)
Vì x>0 nên: \({S_1} = \int\limits_0^{\sqrt 2 } {\left| {2 - {x^2}} \right|dx} = \dfrac{{4\sqrt 2 }}{3}\)
\({S_2} = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\)
Bước 3: Tính \({S_1} - {S_2}\)
\({S_1} - {S_2} = - \dfrac{1}{2} + \dfrac{{4\sqrt 2 }}{3}\)
Hướng dẫn giải:
Bước 1: Tách hình tô đậm thành hiệu của hai hình: \({S_1} - {S_2}\). Trong đó \({S_1}\) là phần tạo bởi các đường \(x = 0;y = 2;y = {x^2}\). \({S_2}\) là phần tạo bởi các đường \(x = 0;y = 2;y = x + 1\).
Bước 2: Tính \({S_1};{S_2}\)
Bước 3: Tính \({S_1} - {S_2}\)