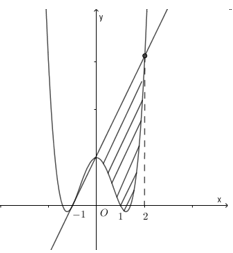
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong \(y = {x^3} - x\) và \(y = x - {x^2}\):
Trả lời bởi giáo viên
Xét phương trình hoành độ giao điểm \({x^3} - x = x - {x^2} \Leftrightarrow {x^3} + {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 2\end{array} \right.\).
Diện tích hình phẳng giới hạn bởi hai đường cong \(y = {x^3} - x\) và \(y = x - {x^2}\) là:
\(S = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right| + \left| {\int\limits_0^1 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right| = \frac{8}{3} + \frac{5}{{12}} = \frac{{37}}{{12}}\)
Hướng dẫn giải:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \(y = f(x),{\mkern 1mu} {\mkern 1mu} y = g(x)\), trục hoành và hai đường thẳng \(x = a;{\mkern 1mu} {\mkern 1mu} x = b\) được tính theo công thức : \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)